10.2 直方图 同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
10.2 直方图
一、选择题
在一个频数分布表中,有 个数据,各组的频数之和等于
A. B. C. D.
某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有 人,则其中成绩为“良”和“优”的总人数估计为
A. B. C. D.
某校有 名学生参加毕业会考,其中数学成绩在 分之间的共有 人,这个分数段的百分比为
A. B. C. D.
为了解某校学生 年五一期间参加社团活动时间的情况,随机抽查了其中 名学生进行统计,并绘制成如图所示的频数直方图.已知该校共有 名学生,据此估计,该校五一期间参加社团活动时间在 小时之间的学生数大约是
A. B. C. D.
在画频数分布直方图时,一组数据的最小值为 ,最大值是 ,若确定组距为 ,则分成的组数是
A. B. C. D.
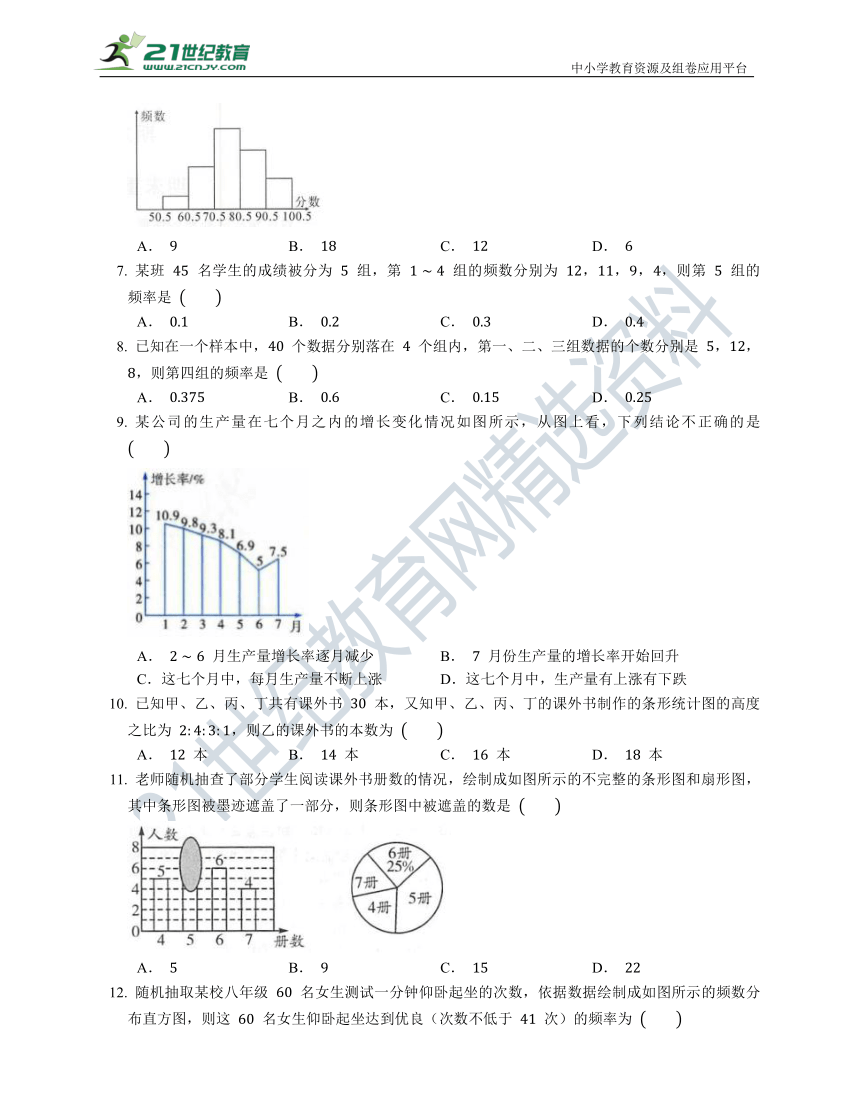
某班有 位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图(横轴表示分数,把 分到 分之间的分数分成 组,组距是 分,纵轴表示频数)如图所示,从左到右的小长方形的高度比是 ,则由图可知,其中分数在 之间的人数是
A. B. C. D.
某班 名学生的成绩被分为 组,第 组的频数分别为 ,,,,则第 组的频率是
A. B. C. D.
已知在一个样本中, 个数据分别落在 个组内,第一、二、三组数据的个数分别是 ,,,则第四组的频率是
A. B. C. D.
某公司的生产量在七个月之内的增长变化情况如图所示,从图上看,下列结论不正确的是
A. 月生产量增长率逐月减少 B. 月份生产量的增长率开始回升
C.这七个月中,每月生产量不断上涨 D.这七个月中,生产量有上涨有下跌
已知甲、乙、丙、丁共有课外书 本,又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为 ,则乙的课外书的本数为
A. 本 B. 本 C. 本 D. 本
老师随机抽查了部分学生阅读课外书册数的情况,绘制成如图所示的不完整的条形图和扇形图,其中条形图被墨迹遮盖了一部分,则条形图中被遮盖的数是
A. B. C. D.
随机抽取某校八年级 名女生测试一分钟仰卧起坐的次数,依据数据绘制成如图所示的频数分布直方图,则这 名女生仰卧起坐达到优良(次数不低于 次)的频率为
A. B. C. D.
二、填空题
要了解全市中考生的数学成绩在某一范围内的学生所占比例的大小,需知道相应样本的 (填“平均数”、“方差”或“频率分布”).
有 个数据,落在某一小组内的频数与总数之比是 ,那么在这 个数据中,落在这一小组内的数据的频数是 .
为了帮助班上的两名贫困学生解决经济困难,班上的 名学生捐出了零花钱,他们的捐款数(单位:元)如下:,,,,,,,,,,,,,,,,,,,.班主任老师准备将这组数据制成频数分布直方图,以表彰他们的爱心,制图时先计算最大值与最小值的差: .若取组距为 ,则应分成 组;若第一组的起点定为 ,则在 范围内的频数为 .
为了支援地震灾区同学,某校开展捐书活动,九()班同学积极参与.现将捐书数量绘制成频数分布直方图(如图所示).如果捐书数量在 组别的频率是 .那么捐书数量在 组别的有 人.
根据下列统计图(如图),回答问题:
该超市 月份的水果类销售额 月份的水果类销售额(请从“”“”“”中选一个填空).
某养猪场对 头生猪的质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在 及以上的生猪有 头.
低碳发展是某市市政府工作报告提出的发展理念.近期,某区与某技术支持单位合作,组织策划了该区“低碳先锋行动”,开展低碳测量和排行活动.根据调查数据制作了频数分布直方图和扇形统计图,图 ① 中从左到右各长方形的高度之比为
()已知碳排放值 的单位有 个,则此次行动调查了 个单位;
()在图②中,碳排放值 部分的圆心角为 度;
()小明把图①中碳排放值 的都看成 ,碳排放值 的都看成 ,以此类推,若每个被检单位的建筑面积均为 平方米,则按小明的办法,可估算碳排放值 的被检单位一个月的碳排放总值约为 吨.
三、解答题
在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分,某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知 , 两组户数频数直方图的高度比为 .
请结合图表中相关数据解答下列问题:
(1) 这次接受调查的有 户;
(2) 在扇形统计图中,“”组所对应的圆心角的度数是 ;
(3) 请你补全频数直方图;
(4) 若该社区有 户住户,请估计月信息消费额不少于 元的户数是多少?
某工厂生产某种产品, 月份的产量为 件, 月份的产量为 件,用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于 分的产品为合格产品.
(1) 求 月份生产的该产品抽样检测的合格率.
(2) 在 月份和 月份生产的产品中,估计哪个月的不合格件数较多?为什么?
暑期将至,某校组织学生进行“防溺水”安全知识竞赛,老师从中随机抽取了部分学生的成绩(得分取整数,满分为 分),整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图.
其中 组的频数 比 组的频数 小 .请根据以上信息,解答下列问题:
(1) 本次共抽取 名学生, 的值为 ;
(2) 在扇形统计图中, , 组所占比例为 ;
(3) 补全频数分布直方图;
(4) 若全校共有 名学生,请根据抽样调查的结果,估计成绩在 分以上的学生人数.
为了了解某校某年级 名学生一分钟的跳绳次数,从中随机抽取了 名学生的一分钟跳绳次数(次数为整数,且最高次数不超过 次),整理后绘制成如图所示的频数分布直方图,图中的 , 满足关系式 ,后来由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于 .请结合所给条件,回答下列问题.
(1) 求问题中的总体和样本容量;
(2) 求 , 的值(请写出必要的计算过程);
(3) 如果一分钟跳绳次数在 次以上为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的有多少人.(注:该年级共 名学生)
某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为 类,每车乘坐 人、 人、 人、 人、 人分别记为 ,,,,,由调查所得数据绘制了如图所示的不完整的统计图表.
(1) 求本次调查的小型汽车数量及 , 的值;
(2) 补全频数分布直方图;
(3) 若某时段通过该路段的小型汽车数量为 辆,请你估计其中每车只乘坐 人的小型汽车数量.
某工厂生产某种产品, 月份的产量为 件, 月份的产量为 件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于 分的产品为合格产品.
【思路导引】
合格率 .
(1) 求 月份生产的该产品抽样检测的合格率;
(2) 在 月份和 月份生产的产品中,估计哪个月的不合格件数最多?为什么?
答案
一、选择题
1. 【答案】A
2. 【答案】A
【解析】“良”和“优”的人数所占的百分比:,
在 人中成绩为“良”和“优”的总人数估计为 (人).
3. 【答案】B
4. 【答案】A
5. 【答案】A
6. 【答案】B
7. 【答案】B
8. 【答案】A
9. 【答案】D
10. 【答案】A
11. 【答案】B
【解析】由题中条形图和扇形图,得抽查的学生人数为 ,
阅读 册的学生人数为 .
12. 【答案】B
二、填空题
13. 【答案】频率分布
14. 【答案】
15. 【答案】;;
16. 【答案】
17. 【答案】
【解析】 月份的水果类销售额 (万元)
月份的水果类销售额 (万元),
所以 月份的水果类销售额 月份的水果类销售额.
18. 【答案】
19. 【答案】 ; ;
三、解答题
20. 【答案】
(1)
(2)
(3) 略
(4) .
21. 【答案】
(1) 因为 .
答: 月份生产的该产品抽样检测的合格率是 .
(2) 月份生产的产品中,不合格的件数是 ,
月份生产的产品中,不合格的件数是 ,
因为 ,
所以估计 月份生产的产品中不合格的件数较多.
22. 【答案】
(1) ;
(2) ;
(3) (人),
“ 组”频数为 (人),
“ 组”频数为 (人),
补全频数分布直方图如图所示:
(4) (人).
答:估计成绩在 分以上的学生人数大约为 人.
【解析】
(1) 组的频数 比 组的频数 小 ,
组的频率比 组的频率小 ,
因此调查人数为 (人),
(人).
故答案为 ,;
(2) ,
即 .
“ 组”所占的百分比为 .
故答案为 ,;
23. 【答案】
(1) 名学生一分钟的跳绳次数是总体,样本容量是 .
(2) 由题中所给数据可知 的有 人, 的有 人,
.
,
,.
(3) (人)
答:估计该校该年级学生跳绳成绩优秀的有 人.
24. 【答案】
(1) 本次调查的小型汽车数量为 (辆),
,.
(2) 类小汽车的数量为 (辆), 类小汽车的数量为 (辆),
补全图形如下:
(3) 每车只乘坐 人的小型汽车数量为 (辆).
25. 【答案】
(1) .
答: 月份生产的该产品抽样检测的合格率是 .
(2) 月份生产的产品中,不合格的件数是 (件)
月份生产的产品中,不合格的件数是 ,
,
估计 月份生产的产品中不合格的件数多.
10.2 直方图
一、选择题
在一个频数分布表中,有 个数据,各组的频数之和等于
A. B. C. D.
某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有 人,则其中成绩为“良”和“优”的总人数估计为
A. B. C. D.
某校有 名学生参加毕业会考,其中数学成绩在 分之间的共有 人,这个分数段的百分比为
A. B. C. D.
为了解某校学生 年五一期间参加社团活动时间的情况,随机抽查了其中 名学生进行统计,并绘制成如图所示的频数直方图.已知该校共有 名学生,据此估计,该校五一期间参加社团活动时间在 小时之间的学生数大约是
A. B. C. D.
在画频数分布直方图时,一组数据的最小值为 ,最大值是 ,若确定组距为 ,则分成的组数是
A. B. C. D.
某班有 位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图(横轴表示分数,把 分到 分之间的分数分成 组,组距是 分,纵轴表示频数)如图所示,从左到右的小长方形的高度比是 ,则由图可知,其中分数在 之间的人数是
A. B. C. D.
某班 名学生的成绩被分为 组,第 组的频数分别为 ,,,,则第 组的频率是
A. B. C. D.
已知在一个样本中, 个数据分别落在 个组内,第一、二、三组数据的个数分别是 ,,,则第四组的频率是
A. B. C. D.
某公司的生产量在七个月之内的增长变化情况如图所示,从图上看,下列结论不正确的是
A. 月生产量增长率逐月减少 B. 月份生产量的增长率开始回升
C.这七个月中,每月生产量不断上涨 D.这七个月中,生产量有上涨有下跌
已知甲、乙、丙、丁共有课外书 本,又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为 ,则乙的课外书的本数为
A. 本 B. 本 C. 本 D. 本
老师随机抽查了部分学生阅读课外书册数的情况,绘制成如图所示的不完整的条形图和扇形图,其中条形图被墨迹遮盖了一部分,则条形图中被遮盖的数是
A. B. C. D.
随机抽取某校八年级 名女生测试一分钟仰卧起坐的次数,依据数据绘制成如图所示的频数分布直方图,则这 名女生仰卧起坐达到优良(次数不低于 次)的频率为
A. B. C. D.
二、填空题
要了解全市中考生的数学成绩在某一范围内的学生所占比例的大小,需知道相应样本的 (填“平均数”、“方差”或“频率分布”).
有 个数据,落在某一小组内的频数与总数之比是 ,那么在这 个数据中,落在这一小组内的数据的频数是 .
为了帮助班上的两名贫困学生解决经济困难,班上的 名学生捐出了零花钱,他们的捐款数(单位:元)如下:,,,,,,,,,,,,,,,,,,,.班主任老师准备将这组数据制成频数分布直方图,以表彰他们的爱心,制图时先计算最大值与最小值的差: .若取组距为 ,则应分成 组;若第一组的起点定为 ,则在 范围内的频数为 .
为了支援地震灾区同学,某校开展捐书活动,九()班同学积极参与.现将捐书数量绘制成频数分布直方图(如图所示).如果捐书数量在 组别的频率是 .那么捐书数量在 组别的有 人.
根据下列统计图(如图),回答问题:
该超市 月份的水果类销售额 月份的水果类销售额(请从“”“”“”中选一个填空).
某养猪场对 头生猪的质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在 及以上的生猪有 头.
低碳发展是某市市政府工作报告提出的发展理念.近期,某区与某技术支持单位合作,组织策划了该区“低碳先锋行动”,开展低碳测量和排行活动.根据调查数据制作了频数分布直方图和扇形统计图,图 ① 中从左到右各长方形的高度之比为
()已知碳排放值 的单位有 个,则此次行动调查了 个单位;
()在图②中,碳排放值 部分的圆心角为 度;
()小明把图①中碳排放值 的都看成 ,碳排放值 的都看成 ,以此类推,若每个被检单位的建筑面积均为 平方米,则按小明的办法,可估算碳排放值 的被检单位一个月的碳排放总值约为 吨.
三、解答题
在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分,某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知 , 两组户数频数直方图的高度比为 .
请结合图表中相关数据解答下列问题:
(1) 这次接受调查的有 户;
(2) 在扇形统计图中,“”组所对应的圆心角的度数是 ;
(3) 请你补全频数直方图;
(4) 若该社区有 户住户,请估计月信息消费额不少于 元的户数是多少?
某工厂生产某种产品, 月份的产量为 件, 月份的产量为 件,用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于 分的产品为合格产品.
(1) 求 月份生产的该产品抽样检测的合格率.
(2) 在 月份和 月份生产的产品中,估计哪个月的不合格件数较多?为什么?
暑期将至,某校组织学生进行“防溺水”安全知识竞赛,老师从中随机抽取了部分学生的成绩(得分取整数,满分为 分),整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图.
其中 组的频数 比 组的频数 小 .请根据以上信息,解答下列问题:
(1) 本次共抽取 名学生, 的值为 ;
(2) 在扇形统计图中, , 组所占比例为 ;
(3) 补全频数分布直方图;
(4) 若全校共有 名学生,请根据抽样调查的结果,估计成绩在 分以上的学生人数.
为了了解某校某年级 名学生一分钟的跳绳次数,从中随机抽取了 名学生的一分钟跳绳次数(次数为整数,且最高次数不超过 次),整理后绘制成如图所示的频数分布直方图,图中的 , 满足关系式 ,后来由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于 .请结合所给条件,回答下列问题.
(1) 求问题中的总体和样本容量;
(2) 求 , 的值(请写出必要的计算过程);
(3) 如果一分钟跳绳次数在 次以上为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的有多少人.(注:该年级共 名学生)
某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为 类,每车乘坐 人、 人、 人、 人、 人分别记为 ,,,,,由调查所得数据绘制了如图所示的不完整的统计图表.
(1) 求本次调查的小型汽车数量及 , 的值;
(2) 补全频数分布直方图;
(3) 若某时段通过该路段的小型汽车数量为 辆,请你估计其中每车只乘坐 人的小型汽车数量.
某工厂生产某种产品, 月份的产量为 件, 月份的产量为 件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于 分的产品为合格产品.
【思路导引】
合格率 .
(1) 求 月份生产的该产品抽样检测的合格率;
(2) 在 月份和 月份生产的产品中,估计哪个月的不合格件数最多?为什么?
答案
一、选择题
1. 【答案】A
2. 【答案】A
【解析】“良”和“优”的人数所占的百分比:,
在 人中成绩为“良”和“优”的总人数估计为 (人).
3. 【答案】B
4. 【答案】A
5. 【答案】A
6. 【答案】B
7. 【答案】B
8. 【答案】A
9. 【答案】D
10. 【答案】A
11. 【答案】B
【解析】由题中条形图和扇形图,得抽查的学生人数为 ,
阅读 册的学生人数为 .
12. 【答案】B
二、填空题
13. 【答案】频率分布
14. 【答案】
15. 【答案】;;
16. 【答案】
17. 【答案】
【解析】 月份的水果类销售额 (万元)
月份的水果类销售额 (万元),
所以 月份的水果类销售额 月份的水果类销售额.
18. 【答案】
19. 【答案】 ; ;
三、解答题
20. 【答案】
(1)
(2)
(3) 略
(4) .
21. 【答案】
(1) 因为 .
答: 月份生产的该产品抽样检测的合格率是 .
(2) 月份生产的产品中,不合格的件数是 ,
月份生产的产品中,不合格的件数是 ,
因为 ,
所以估计 月份生产的产品中不合格的件数较多.
22. 【答案】
(1) ;
(2) ;
(3) (人),
“ 组”频数为 (人),
“ 组”频数为 (人),
补全频数分布直方图如图所示:
(4) (人).
答:估计成绩在 分以上的学生人数大约为 人.
【解析】
(1) 组的频数 比 组的频数 小 ,
组的频率比 组的频率小 ,
因此调查人数为 (人),
(人).
故答案为 ,;
(2) ,
即 .
“ 组”所占的百分比为 .
故答案为 ,;
23. 【答案】
(1) 名学生一分钟的跳绳次数是总体,样本容量是 .
(2) 由题中所给数据可知 的有 人, 的有 人,
.
,
,.
(3) (人)
答:估计该校该年级学生跳绳成绩优秀的有 人.
24. 【答案】
(1) 本次调查的小型汽车数量为 (辆),
,.
(2) 类小汽车的数量为 (辆), 类小汽车的数量为 (辆),
补全图形如下:
(3) 每车只乘坐 人的小型汽车数量为 (辆).
25. 【答案】
(1) .
答: 月份生产的该产品抽样检测的合格率是 .
(2) 月份生产的产品中,不合格的件数是 (件)
月份生产的产品中,不合格的件数是 ,
,
估计 月份生产的产品中不合格的件数多.
