苏教版小学数学五年级下册7.《解决问题的策略综合练习1》(含答案)
文档属性
| 名称 | 苏教版小学数学五年级下册7.《解决问题的策略综合练习1》(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 619.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 22:47:03 | ||
图片预览


文档简介
《解决问题的策略综合练习1》
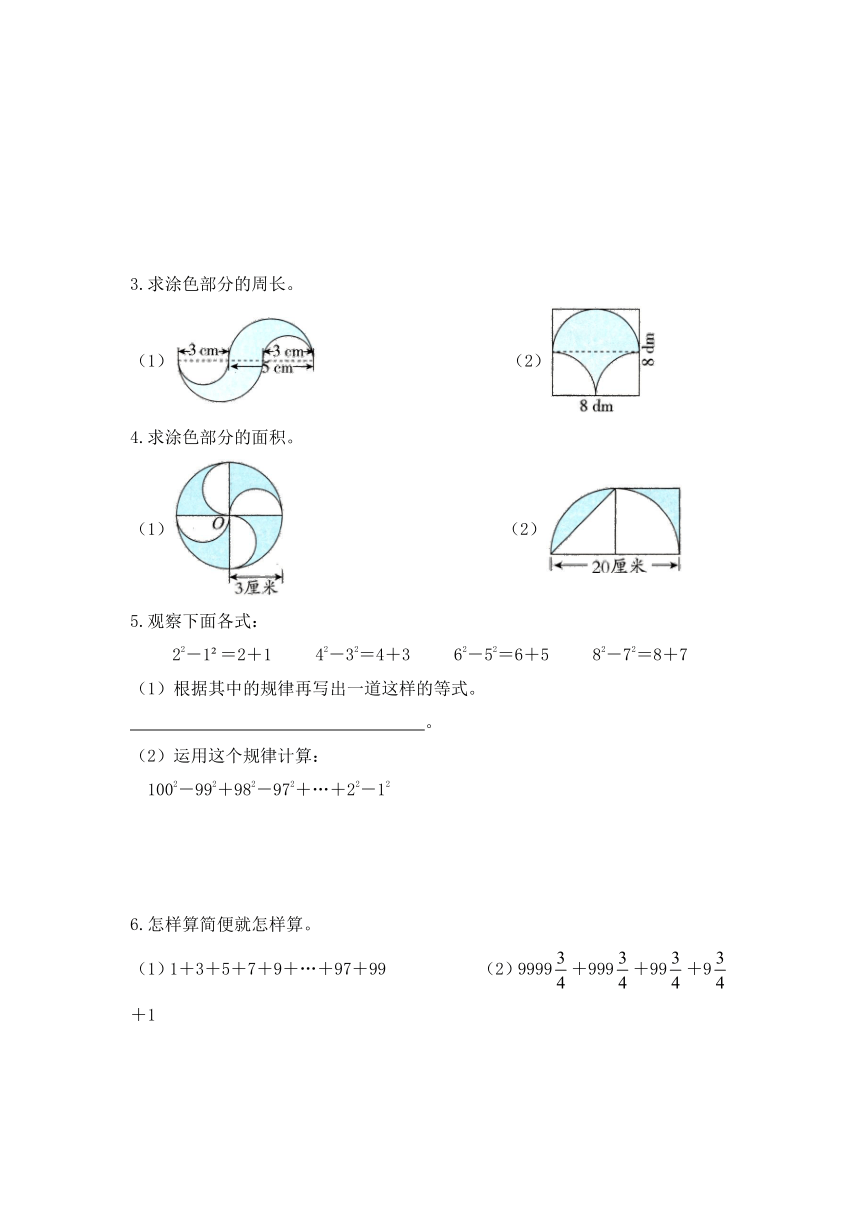
1.填空。
(1)推导平面图形面积公式时,经常用到转化思想,请你结合平行四边形和圆面积公式推导过程填空。
a =( )cm h =( )cm a =( )dm h =( )dm
(2)下边涂色部分的周长可以转化为长( )厘米、宽( )厘米的长方形的周长。(每个小方格都表示边长为1厘米的正方形)
(3)有8支排球队参加女排大奖赛,比赛以单场淘汰制晋级,一共要进行( )场比赛才能产生冠军。如果是32支排球队参赛,那么需进行( )场比赛才能产生冠军。
(4)如下图,已知AB=40厘米,则各圆的周长和是( )厘米。
2.怎样简便就怎样算。
(1)3.85×9.9+0.01×38.5 (2)1-----
(3)已知=-,=-,那么=-。
根据发现的规律计算+++。
3.求涂色部分的周长。
(1) (2)
4.求涂色部分的面积。
(1) (2)
5.观察下面各式:
22-1 =2+1 42-32=4+3 62-52=6+5 82-72=8+7
(1)根据其中的规律再写出一道这样的等式。
。
(2)运用这个规律计算:
1002-992+982-972+…+22-12
6.怎样算简便就怎样算。
(1)1+3+5+7+9+…+97+99 (2)9999+999+99+9+1
(3)++++
7.有64支球队参加比赛,以单场淘汰制(即每场比赛淘汰一支球队)进行。如果要决出冠军,那么一共要比赛多少场?
8.下面长方形的长是9厘米,截去一个最大的正方形,求剩下部分的周长。
9.如图,月城广场中间的健身场地是由5个大小相同的正方形重合而成,其中每个正方形的顶点都在另一个正方形的中心上。如果每个正方形的边长是40米,那么沿健身场地走一圈要走多少米?
10.如图,涂色三角形甲的面积比涂色三角形乙的面积大多少平方分米?
11.如图是由4个半径都是4厘米的圆组成的,正方形的顶点正好是4个圆的圆心。求阴影部分的面积。(得数保留π)
12.公园里有一个花坛(如下图)。花坛中正方形的边长为8米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。这个花坛的面积约是多少平方米?(得数保留整数)
参考答案
1.(1)12 9 12.56 4 (2)6 3 (3)7 31 (4)125.6
2.(1)3.85×9.9+0.01×38.5=3.85×9.9+0.1×3.85=3.85×(9.9+0.1)=3.85×10=38.5
(2)1-----=1+-(+++++)=-(1-)
=-=
(3)4 5
+++=-+-+-+-=-=
3.(1)3.14×3+3.14×5=25.12(cm) (2)3.14×8=25.12(dm)
4.(1)3.14×32-3.14×(3÷2)2×2=14.13(平方厘米) (2)(20÷2)2÷2=50(平方厘米)
5.(1)答案不唯一,如:132-122=13+12
(2)1002-992+982-972+…+22-12=100+99+98+97+…+2+1=(1+100)×100÷2=5050
6.(1)原式=(1+99)×50÷2=2500
(2)原式=(9999+)+(999+)+(99+)+(9+)
=10000+1000+100+10=11110
(3)原式=-+-+-+-+-=-=
7.64-1=63(场) 答:一共要比赛63场。
8.9×2=18(厘米) 提示:剩下的长方形的相邻两条边的长度和等于原长方形的长。
9.40×4×3=480(米) 提示:通过平移线段,将健身场地的周长转化成3个正方形的周长。
10.12×9÷2-12×6÷2=18(平方分米)
答:涂色三角形甲的面积比涂色三角形乙的面积大18平方分米。
11.(4+4)2-π×42=(64-16π)(平方厘米)
64-16π+π×42×3=(64+32π)(平方厘米)
提示:可以先用正方形的面积减去1个圆的面积得中间的阴影部分的面积,再与3个圆的面积和相加得到阴影部分的面积。
12.8×8+3.14×3 ×(4-1)≈149(平方米) 答:这个花坛的面积约是149平方米。
1.填空。
(1)推导平面图形面积公式时,经常用到转化思想,请你结合平行四边形和圆面积公式推导过程填空。
a =( )cm h =( )cm a =( )dm h =( )dm
(2)下边涂色部分的周长可以转化为长( )厘米、宽( )厘米的长方形的周长。(每个小方格都表示边长为1厘米的正方形)
(3)有8支排球队参加女排大奖赛,比赛以单场淘汰制晋级,一共要进行( )场比赛才能产生冠军。如果是32支排球队参赛,那么需进行( )场比赛才能产生冠军。
(4)如下图,已知AB=40厘米,则各圆的周长和是( )厘米。
2.怎样简便就怎样算。
(1)3.85×9.9+0.01×38.5 (2)1-----
(3)已知=-,=-,那么=-。
根据发现的规律计算+++。
3.求涂色部分的周长。
(1) (2)
4.求涂色部分的面积。
(1) (2)
5.观察下面各式:
22-1 =2+1 42-32=4+3 62-52=6+5 82-72=8+7
(1)根据其中的规律再写出一道这样的等式。
。
(2)运用这个规律计算:
1002-992+982-972+…+22-12
6.怎样算简便就怎样算。
(1)1+3+5+7+9+…+97+99 (2)9999+999+99+9+1
(3)++++
7.有64支球队参加比赛,以单场淘汰制(即每场比赛淘汰一支球队)进行。如果要决出冠军,那么一共要比赛多少场?
8.下面长方形的长是9厘米,截去一个最大的正方形,求剩下部分的周长。
9.如图,月城广场中间的健身场地是由5个大小相同的正方形重合而成,其中每个正方形的顶点都在另一个正方形的中心上。如果每个正方形的边长是40米,那么沿健身场地走一圈要走多少米?
10.如图,涂色三角形甲的面积比涂色三角形乙的面积大多少平方分米?
11.如图是由4个半径都是4厘米的圆组成的,正方形的顶点正好是4个圆的圆心。求阴影部分的面积。(得数保留π)
12.公园里有一个花坛(如下图)。花坛中正方形的边长为8米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。这个花坛的面积约是多少平方米?(得数保留整数)
参考答案
1.(1)12 9 12.56 4 (2)6 3 (3)7 31 (4)125.6
2.(1)3.85×9.9+0.01×38.5=3.85×9.9+0.1×3.85=3.85×(9.9+0.1)=3.85×10=38.5
(2)1-----=1+-(+++++)=-(1-)
=-=
(3)4 5
+++=-+-+-+-=-=
3.(1)3.14×3+3.14×5=25.12(cm) (2)3.14×8=25.12(dm)
4.(1)3.14×32-3.14×(3÷2)2×2=14.13(平方厘米) (2)(20÷2)2÷2=50(平方厘米)
5.(1)答案不唯一,如:132-122=13+12
(2)1002-992+982-972+…+22-12=100+99+98+97+…+2+1=(1+100)×100÷2=5050
6.(1)原式=(1+99)×50÷2=2500
(2)原式=(9999+)+(999+)+(99+)+(9+)
=10000+1000+100+10=11110
(3)原式=-+-+-+-+-=-=
7.64-1=63(场) 答:一共要比赛63场。
8.9×2=18(厘米) 提示:剩下的长方形的相邻两条边的长度和等于原长方形的长。
9.40×4×3=480(米) 提示:通过平移线段,将健身场地的周长转化成3个正方形的周长。
10.12×9÷2-12×6÷2=18(平方分米)
答:涂色三角形甲的面积比涂色三角形乙的面积大18平方分米。
11.(4+4)2-π×42=(64-16π)(平方厘米)
64-16π+π×42×3=(64+32π)(平方厘米)
提示:可以先用正方形的面积减去1个圆的面积得中间的阴影部分的面积,再与3个圆的面积和相加得到阴影部分的面积。
12.8×8+3.14×3 ×(4-1)≈149(平方米) 答:这个花坛的面积约是149平方米。
