20.2 数据的波动程度 同步练习(含答案)
文档属性
| 名称 | 20.2 数据的波动程度 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 116.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 07:08:44 | ||
图片预览

文档简介
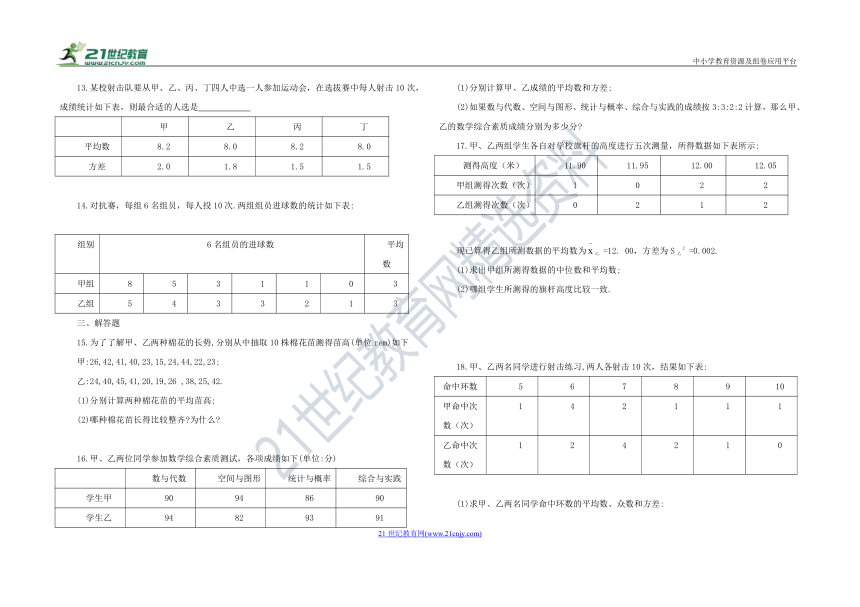
中小学教育资源及组卷应用平台
八年级下册数学20.2 数据的波动程度 同步练习
一、选择题
1.在方差的计算公式S2=[(x1-20)2+(x2-20)+……+(x10-20)2]中,数字10和20分别表示( )
A.数据的个数和方差 B.平均数和数据个数
C.数据的个数和平均数 D.数据的方差和平均数
2.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位的更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
3.甲、乙两组数据的平均数相等,甲组数据的方差S甲2=0.050,乙组数据的方差S乙2=0.055,则( )
A.甲组数据比乙组数据波动大 B.乙组数据比甲组数据波动大
C.甲组数据与乙组数据的波动一样大 D.甲,乙两组数据的数据波动不能比较
4.小明和小强同学分别统计了自己最近10次“一分钟跳绳”的成绩,下列统计量中能用来比较两人成绩稳定程度的是( )
A.平均数 B.中位数 C.方差 D.众数
5.如果一组数据x1,x2,……xn的方差是3,则另组数据2x1 +5,2x2+5,……2xn +5的方差是( )
A.3 B.6 C.8 D.12
6.在一次射击练习中,甲、乙两人前5次射击的成绩分别如下(单位:环):甲:10,8,10,10,7;
乙:7,10,9,9,10,则这次练习中,甲、乙两人方差的大小关系是( )
A.S甲2> S乙2 B. S甲2< S乙2 C.S甲2= S乙2 D.无法确定
7.为了了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民4月份用电量的调查结果:
居民(户) 1 3 2 4
月用电量(度/户) 40 50 55 60
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是55度 B.众数是60度
C.方差是29 D.平均数是54度
8.8月26日,第二届青奥会将在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备。
在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11,0.03,0.05,0.02,则当天这四位运动员“110米跨栏”的训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
9.有11位同学参加学校举行的歌唱比赛,比赛后根据每个学生的最后得分计算出中位数、平均数、众数和方整,如果去掉一个最高分和一个最低分,则一定不会发生变化的是( )
A.中位数 B.平均数 C.众数 D.方差
二、填空题
10.已知一组数据-3,x,2,3,1,6的中位数为1,则其方差为 .
11.一组数据3,4,5,x,7,8的平均数是6,则其方差是
12.甲、乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为9,8,9,6,10,6,甲、乙两人平均成绩相等,乙成绩的方差为4.那么成绩较为稳定的是 . (填“甲”或“乙”)
13.某校射击队要从甲、乙、丙、丁四人中选一人参加运动会,在选拔赛中每人射击10次,成绩统计如下表,则最合适的人选是
甲 乙 丙 丁
平均数 8.2 8.0 8.2 8.0
方差 2.0 1.8 1.5 1.5
14.对抗赛,每组6名组员,每人投10次.两组组员进球数的统计如下表:
组别 6名组员的进球数 平均数
甲组 8 5 3 1 1 0 3
乙组 5 4 3 3 2 1 3
三、解答题
15.为了了解甲、乙两种棉花的长势,分别从中抽取10株棉花苗测得苗高(单位rem)如下
甲:26,42,41,40,23,15,24,44,22,23;
乙:24,40,45,41,20,19,26 ,38,25,42.
(1)分别计算两种棉花苗的平均苗高;
(2)哪种棉花苗长得比较整齐 为什么
16.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 94 86 90
学生乙 94 82 93 91
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分
17.甲、乙两组学生各自对学校旗杆的高度进行五次测量,所得数据如下表所示:
测得高度(米) 11.90 11.95 12.00 12.05
甲组测得次数(次) 1 0 2 2
乙组测得次数(次) 0 2 1 2
现已算得乙组所测数据的平均数为乙 =12. 00,方差为S乙2 =0.002.
(1)求出甲组所测得数据的中位数和平均数;
(2)哪组学生所测得的旗杆高度比较一致.
18.甲、乙两名同学进行射击练习,两人各射击10次,结果如下表:
命中环数 5 6 7 8 9 10
甲命中次数(次) 1 4 2 1 1 1
乙命中次数(次) 1 2 4 2 1 0
(1)求甲、乙两名同学命中环数的平均数、众数和方差:
(2)根据所学知识,如果从两人中选取一人参加比赛,应选哪一位 为什么
19.八年级(2)班组织了一次经典诵读比赛,甲乙两队各10人的比赛成绩如下表:
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数局 分,乙队成绩的众数是 分.
(2)计算乙队的平均成绩和方差;
(3)已如甲队成绩的方差是1.4.则成绩较为整齐的是 队。
20某班级从甲、乙两位同学中选派一人参加“秀美山河”知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,并计算出甲成绩的平均数是80,甲、乙成绩的方差分别是320,40,但绘制的统计图尚不完整。
甲、乙两人模拟成绩统计表
第1次 第2次 第3次 第4次 第5次
甲成绩 90 100 90 50 a
乙成绩 80 70 80 90 80
根据以上信息,请你解答下列问题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中
四、中考链接
21.(赤峰中考)学校朗诵比赛,共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉一个最高分,一个最低分,得到7个有效评分,7个有效评分与9个原始评分相比,不变的数据特征是( )
A.平均数 B.中位数 C.众数 D.方差
参考答案:
C 2.C 3.B 4.C 5.D 6.A 7.C 8.D 9.A
10.9
甲
丙
乙
15.解:(1)甲 =30;乙 =32.
(2)S甲2 = 100,S乙2 =91.2,
∵S甲2 >S乙2 乙种棉花苗长得比较整齐.
16.解:(1)甲成绩的平均数为X (90+94+86+90)=90(分),
甲成绩的方差为x[(90- 90)2X2+(94-90)*+ (86- 90)*]=8;
乙成绩的平均数为X (94+82+93+91)=90(分),
乙成绩的方差为X[(94-90)+(82- 90)2+(93-90)2+(91-90)*]=22.5.
(2)甲的综合成绩为X (90X3+94X3+ 86X2+90X2)=90.4(分),
乙的综合成绩为X (94X3+82X3+93X2+91X2)=89.6(分).
17.解:(1)甲组中位数:12.00;平均数:12.00.
(2)S甲2 =0.003,S甲2 >S乙2
∴乙组同学所测旗杆高度比较一致.
18.解:(1)甲:甲=7,众数:6,方差:S甲2 =2.2.
乙:乙 =7,众数:7,方差:S乙2 =1.2.
(2)应选乙参加比赛,因为两人命中环数的平均数相同,众数乙大,从方差上看乙成绩稳定。
19.(1)9.5,10
(2)乙 =9分,S乙2=1
(3)乙
20.解:(1)70
(2)如图所示,
(3)乙= (80+70+80+ 90+80) =80.
(4)甲,乙成绩的平均数相同,乙的方差小于甲的方差,乙比甲稳定,所以乙将被选中。
21.B
21世纪教育网(www.21cnjy.com)
八年级下册数学20.2 数据的波动程度 同步练习
一、选择题
1.在方差的计算公式S2=[(x1-20)2+(x2-20)+……+(x10-20)2]中,数字10和20分别表示( )
A.数据的个数和方差 B.平均数和数据个数
C.数据的个数和平均数 D.数据的方差和平均数
2.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位的更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
3.甲、乙两组数据的平均数相等,甲组数据的方差S甲2=0.050,乙组数据的方差S乙2=0.055,则( )
A.甲组数据比乙组数据波动大 B.乙组数据比甲组数据波动大
C.甲组数据与乙组数据的波动一样大 D.甲,乙两组数据的数据波动不能比较
4.小明和小强同学分别统计了自己最近10次“一分钟跳绳”的成绩,下列统计量中能用来比较两人成绩稳定程度的是( )
A.平均数 B.中位数 C.方差 D.众数
5.如果一组数据x1,x2,……xn的方差是3,则另组数据2x1 +5,2x2+5,……2xn +5的方差是( )
A.3 B.6 C.8 D.12
6.在一次射击练习中,甲、乙两人前5次射击的成绩分别如下(单位:环):甲:10,8,10,10,7;
乙:7,10,9,9,10,则这次练习中,甲、乙两人方差的大小关系是( )
A.S甲2> S乙2 B. S甲2< S乙2 C.S甲2= S乙2 D.无法确定
7.为了了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民4月份用电量的调查结果:
居民(户) 1 3 2 4
月用电量(度/户) 40 50 55 60
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是55度 B.众数是60度
C.方差是29 D.平均数是54度
8.8月26日,第二届青奥会将在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备。
在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11,0.03,0.05,0.02,则当天这四位运动员“110米跨栏”的训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
9.有11位同学参加学校举行的歌唱比赛,比赛后根据每个学生的最后得分计算出中位数、平均数、众数和方整,如果去掉一个最高分和一个最低分,则一定不会发生变化的是( )
A.中位数 B.平均数 C.众数 D.方差
二、填空题
10.已知一组数据-3,x,2,3,1,6的中位数为1,则其方差为 .
11.一组数据3,4,5,x,7,8的平均数是6,则其方差是
12.甲、乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为9,8,9,6,10,6,甲、乙两人平均成绩相等,乙成绩的方差为4.那么成绩较为稳定的是 . (填“甲”或“乙”)
13.某校射击队要从甲、乙、丙、丁四人中选一人参加运动会,在选拔赛中每人射击10次,成绩统计如下表,则最合适的人选是
甲 乙 丙 丁
平均数 8.2 8.0 8.2 8.0
方差 2.0 1.8 1.5 1.5
14.对抗赛,每组6名组员,每人投10次.两组组员进球数的统计如下表:
组别 6名组员的进球数 平均数
甲组 8 5 3 1 1 0 3
乙组 5 4 3 3 2 1 3
三、解答题
15.为了了解甲、乙两种棉花的长势,分别从中抽取10株棉花苗测得苗高(单位rem)如下
甲:26,42,41,40,23,15,24,44,22,23;
乙:24,40,45,41,20,19,26 ,38,25,42.
(1)分别计算两种棉花苗的平均苗高;
(2)哪种棉花苗长得比较整齐 为什么
16.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 94 86 90
学生乙 94 82 93 91
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分
17.甲、乙两组学生各自对学校旗杆的高度进行五次测量,所得数据如下表所示:
测得高度(米) 11.90 11.95 12.00 12.05
甲组测得次数(次) 1 0 2 2
乙组测得次数(次) 0 2 1 2
现已算得乙组所测数据的平均数为乙 =12. 00,方差为S乙2 =0.002.
(1)求出甲组所测得数据的中位数和平均数;
(2)哪组学生所测得的旗杆高度比较一致.
18.甲、乙两名同学进行射击练习,两人各射击10次,结果如下表:
命中环数 5 6 7 8 9 10
甲命中次数(次) 1 4 2 1 1 1
乙命中次数(次) 1 2 4 2 1 0
(1)求甲、乙两名同学命中环数的平均数、众数和方差:
(2)根据所学知识,如果从两人中选取一人参加比赛,应选哪一位 为什么
19.八年级(2)班组织了一次经典诵读比赛,甲乙两队各10人的比赛成绩如下表:
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数局 分,乙队成绩的众数是 分.
(2)计算乙队的平均成绩和方差;
(3)已如甲队成绩的方差是1.4.则成绩较为整齐的是 队。
20某班级从甲、乙两位同学中选派一人参加“秀美山河”知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,并计算出甲成绩的平均数是80,甲、乙成绩的方差分别是320,40,但绘制的统计图尚不完整。
甲、乙两人模拟成绩统计表
第1次 第2次 第3次 第4次 第5次
甲成绩 90 100 90 50 a
乙成绩 80 70 80 90 80
根据以上信息,请你解答下列问题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中
四、中考链接
21.(赤峰中考)学校朗诵比赛,共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉一个最高分,一个最低分,得到7个有效评分,7个有效评分与9个原始评分相比,不变的数据特征是( )
A.平均数 B.中位数 C.众数 D.方差
参考答案:
C 2.C 3.B 4.C 5.D 6.A 7.C 8.D 9.A
10.9
甲
丙
乙
15.解:(1)甲 =30;乙 =32.
(2)S甲2 = 100,S乙2 =91.2,
∵S甲2 >S乙2 乙种棉花苗长得比较整齐.
16.解:(1)甲成绩的平均数为X (90+94+86+90)=90(分),
甲成绩的方差为x[(90- 90)2X2+(94-90)*+ (86- 90)*]=8;
乙成绩的平均数为X (94+82+93+91)=90(分),
乙成绩的方差为X[(94-90)+(82- 90)2+(93-90)2+(91-90)*]=22.5.
(2)甲的综合成绩为X (90X3+94X3+ 86X2+90X2)=90.4(分),
乙的综合成绩为X (94X3+82X3+93X2+91X2)=89.6(分).
17.解:(1)甲组中位数:12.00;平均数:12.00.
(2)S甲2 =0.003,S甲2 >S乙2
∴乙组同学所测旗杆高度比较一致.
18.解:(1)甲:甲=7,众数:6,方差:S甲2 =2.2.
乙:乙 =7,众数:7,方差:S乙2 =1.2.
(2)应选乙参加比赛,因为两人命中环数的平均数相同,众数乙大,从方差上看乙成绩稳定。
19.(1)9.5,10
(2)乙 =9分,S乙2=1
(3)乙
20.解:(1)70
(2)如图所示,
(3)乙= (80+70+80+ 90+80) =80.
(4)甲,乙成绩的平均数相同,乙的方差小于甲的方差,乙比甲稳定,所以乙将被选中。
21.B
21世纪教育网(www.21cnjy.com)
