人教版数学七年级下册 8.4三元一次方程组的解法-课件(共26张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.4三元一次方程组的解法-课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 20:37:30 | ||
图片预览








文档简介
(共26张PPT)
三元一次方程组
的解法
知识回顾
()什么叫二元一次方程组?
含有两个未知数,含未知数的项的次数都是.
知识回顾
()什么叫二元一次方程组?
含有两个未知数,含未知数的项的次数都是,并且一共有两个整式方程,像这样的方程组叫做二元一次方程组.
()解二元一次方程组的基本方法有哪几种?它们的实质是什么?
基本方法:代入法和加减法;
实质:消元.
二元一次方程组
一元一次方程
消元
问题探索
小明手头上有张面额分别为元的纸币,共计元.
问题探索
小明手头上有张面额分别为元的纸币,共计元. 其中1元纸币的数量是元纸币数量的倍.
问题探索
小明手头上有张面额分别为元的纸币,共计元. 其中1元纸币的数量是元纸币数量的倍. 求元、元、元纸币各多少张?
解: 元、 元、 元的纸币分别为张,张,张.
,
,
.
三个都是整式方程
新知讲解
含有三个未知数,每个方程中含未知数的项的次数都是.
新知讲解
含有三个未知数,每个方程中含未知数的项的次数都是,并且一共有三个整式方程,像这样的方程组叫做三元一次方程组.
问题探索
,
,
.
①
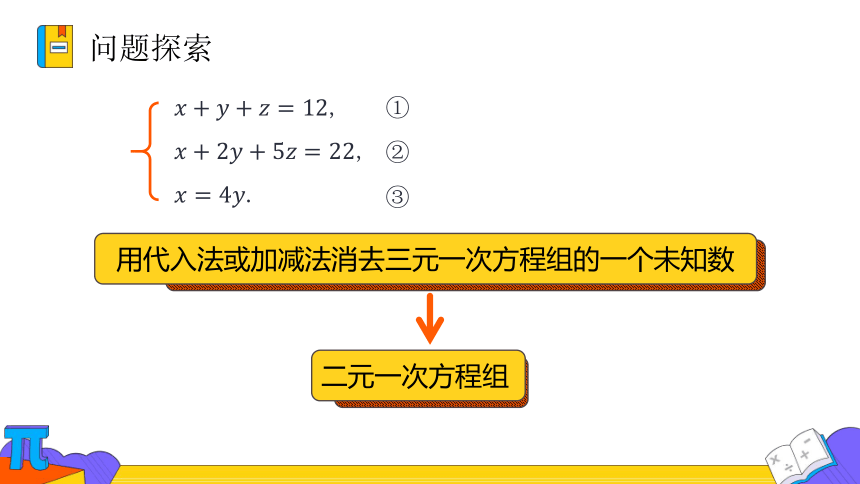
用代入法或加减法消去三元一次方程组的一个未知数
二元一次方程组
问题探索
,
,
.
①
解:把③分别代入①②得:
,
.
它们组成方程组
,
.
④
由④得:⑥
把⑥代入⑤得:
()
把代入③⑥可得:
问题探索
小明手头上有张面额分别为元的纸币,共计元. 其中1元纸币的数量是元纸币数量的倍. 求元、元、元纸币各多少张?
因此,三元一次方程组的解为
答:张.
小结
解三元一次方程组的步骤一般为:
1
利用代入法或加减法,把方程中一个方程与另外两个方程分别组成两组.
小结
解三元一次方程组的步骤一般为:
1
利用代入法或加减法,把方程中一个方程与另外两个方程分别组成两组. 消去两组中的统一未知数,得到关于另外两个未知数的二元一次方程组.
解这个二元一次方程组,求出两个未知数的值.
将求出的两个未知数的值代入原方程中的一个系数比较简单的方程,得到一个一元一次方程.
解一元一次方程,求出最后一个未知数的值.
将求得的未知数的值用“{”合写在一起.
2
3
4
5
小结
三元一次方程组
二元一次方程组
消元
一元一次方程
消元
练习:解三元一次方程组
练习
,
,
.
,
,
.
:
②
由方程③, ④
把④分别代入①②,得
⑤;⑥
由⑤⑥组成二元一次方程组,
解得
练习:解三元一次方程组
练习
,
,
.
,
,
.
:
②
把代入④,得
所以,原方程组的解是
练习:观察下列方程组的特点,如何消元最简单?为什么?
练习
,
,
.
()
②
,
,
.
()
两次消元,可先消去系数较简单的未知数.
②
①+②+③得:.
练习:观察下列方程组的特点,如何消元最简单?为什么?
练习
,
,
.
()
②
,
,
.
()
每两个方程都有两对互为相反数,故两两相加.
②
由①②得:,设.
例题
在等式中,
例题
在等式中,当时,;当时,;当时,.
例题
在等式中,当时,;当时,当时,. 求的值.
,
,
.
:根据题意,得三元一次方程组
②
②
③
⑤
把代入④得:
把 代入①得:
课堂小结
课堂小结
通过这节课的学习,你有什么收获?
1.含有三个未知数,每个方程中含未知数的项的次数都是,
课堂小结
通过这节课的学习,你有什么收获?
1.含有三个未知数,每个方程中含未知数的项的次数都是,并且一共有三个整式方程,像这样的方程组叫做二元一次方程组.
2.解三元一次方程组的基本思想是消元,关键也是消元.
课堂小结
通过这节课的学习,你有什么收获?
1.含有三个未知数,每个方程中含未知数的项的次数都是,并且一共有三个整式方程,像这样的方程组叫做二元一次方程组.
2.解三元一次方程组的基本思想是消元,关键也是消元,我们一定要根据方程组的特点,选准消元对象,定好消元方案.
3.解完后要代入原方程组的三个方程中进行检验.
再 见
三元一次方程组
的解法
知识回顾
()什么叫二元一次方程组?
含有两个未知数,含未知数的项的次数都是.
知识回顾
()什么叫二元一次方程组?
含有两个未知数,含未知数的项的次数都是,并且一共有两个整式方程,像这样的方程组叫做二元一次方程组.
()解二元一次方程组的基本方法有哪几种?它们的实质是什么?
基本方法:代入法和加减法;
实质:消元.
二元一次方程组
一元一次方程
消元
问题探索
小明手头上有张面额分别为元的纸币,共计元.
问题探索
小明手头上有张面额分别为元的纸币,共计元. 其中1元纸币的数量是元纸币数量的倍.
问题探索
小明手头上有张面额分别为元的纸币,共计元. 其中1元纸币的数量是元纸币数量的倍. 求元、元、元纸币各多少张?
解: 元、 元、 元的纸币分别为张,张,张.
,
,
.
三个都是整式方程
新知讲解
含有三个未知数,每个方程中含未知数的项的次数都是.
新知讲解
含有三个未知数,每个方程中含未知数的项的次数都是,并且一共有三个整式方程,像这样的方程组叫做三元一次方程组.
问题探索
,
,
.
①
用代入法或加减法消去三元一次方程组的一个未知数
二元一次方程组
问题探索
,
,
.
①
解:把③分别代入①②得:
,
.
它们组成方程组
,
.
④
由④得:⑥
把⑥代入⑤得:
()
把代入③⑥可得:
问题探索
小明手头上有张面额分别为元的纸币,共计元. 其中1元纸币的数量是元纸币数量的倍. 求元、元、元纸币各多少张?
因此,三元一次方程组的解为
答:张.
小结
解三元一次方程组的步骤一般为:
1
利用代入法或加减法,把方程中一个方程与另外两个方程分别组成两组.
小结
解三元一次方程组的步骤一般为:
1
利用代入法或加减法,把方程中一个方程与另外两个方程分别组成两组. 消去两组中的统一未知数,得到关于另外两个未知数的二元一次方程组.
解这个二元一次方程组,求出两个未知数的值.
将求出的两个未知数的值代入原方程中的一个系数比较简单的方程,得到一个一元一次方程.
解一元一次方程,求出最后一个未知数的值.
将求得的未知数的值用“{”合写在一起.
2
3
4
5
小结
三元一次方程组
二元一次方程组
消元
一元一次方程
消元
练习:解三元一次方程组
练习
,
,
.
,
,
.
:
②
由方程③, ④
把④分别代入①②,得
⑤;⑥
由⑤⑥组成二元一次方程组,
解得
练习:解三元一次方程组
练习
,
,
.
,
,
.
:
②
把代入④,得
所以,原方程组的解是
练习:观察下列方程组的特点,如何消元最简单?为什么?
练习
,
,
.
()
②
,
,
.
()
两次消元,可先消去系数较简单的未知数.
②
①+②+③得:.
练习:观察下列方程组的特点,如何消元最简单?为什么?
练习
,
,
.
()
②
,
,
.
()
每两个方程都有两对互为相反数,故两两相加.
②
由①②得:,设.
例题
在等式中,
例题
在等式中,当时,;当时,;当时,.
例题
在等式中,当时,;当时,当时,. 求的值.
,
,
.
:根据题意,得三元一次方程组
②
②
③
⑤
把代入④得:
把 代入①得:
课堂小结
课堂小结
通过这节课的学习,你有什么收获?
1.含有三个未知数,每个方程中含未知数的项的次数都是,
课堂小结
通过这节课的学习,你有什么收获?
1.含有三个未知数,每个方程中含未知数的项的次数都是,并且一共有三个整式方程,像这样的方程组叫做二元一次方程组.
2.解三元一次方程组的基本思想是消元,关键也是消元.
课堂小结
通过这节课的学习,你有什么收获?
1.含有三个未知数,每个方程中含未知数的项的次数都是,并且一共有三个整式方程,像这样的方程组叫做二元一次方程组.
2.解三元一次方程组的基本思想是消元,关键也是消元,我们一定要根据方程组的特点,选准消元对象,定好消元方案.
3.解完后要代入原方程组的三个方程中进行检验.
再 见
