图形的旋转(江苏省南通市如皋市)
文档属性
| 名称 | 图形的旋转(江苏省南通市如皋市) |

|
|
| 格式 | rar | ||
| 文件大小 | 28.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-06 00:00:00 | ||
图片预览

文档简介
袁桥镇中九年级教学案 2007-9-1
23.1图形的旋转
一、教学目标
教学知识点:1.旋转的定义 2.旋转的基本性质.
能力训练要求:1.通过具体实例认识旋转,理解旋转的基本涵义;
2.通过具体实例认识旋转,知道旋转的性质;
3、经历对具有旋转特征的图形的观察、操作、画图等过程,掌握作图的技能。
二、教学过程:
1、阅读课本P62页“观察”或电脑演示:钟表指针的转动、汽车方向盘的转动、辘轳打水的情景). 问:(1)上面情景中的转动现象,有什么共同特征?
(2)钟表的指针、钟摆在转动过程中,其形状、大小、位置是否发生改变?汽车方向盘的转动呢?
2、归纳旋转的定义:
3、课本P63页练习:学生口答
4、随堂巩固:
(1)下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
(2) 香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,
它是由其中一瓣经过几次旋转得到的?
(3)如图,是△AOB绕点O按逆时针方向旋转450所得的。则点B的对应点是点_____。线段OB的对应线段是线段______。 线段AB的对应线段是线段____。∠A的对应角是______。∠B的对应角是______。旋转中心是点_____。旋转的角度是 ______ _
(4)如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
5、探究活动:(图形见右上)
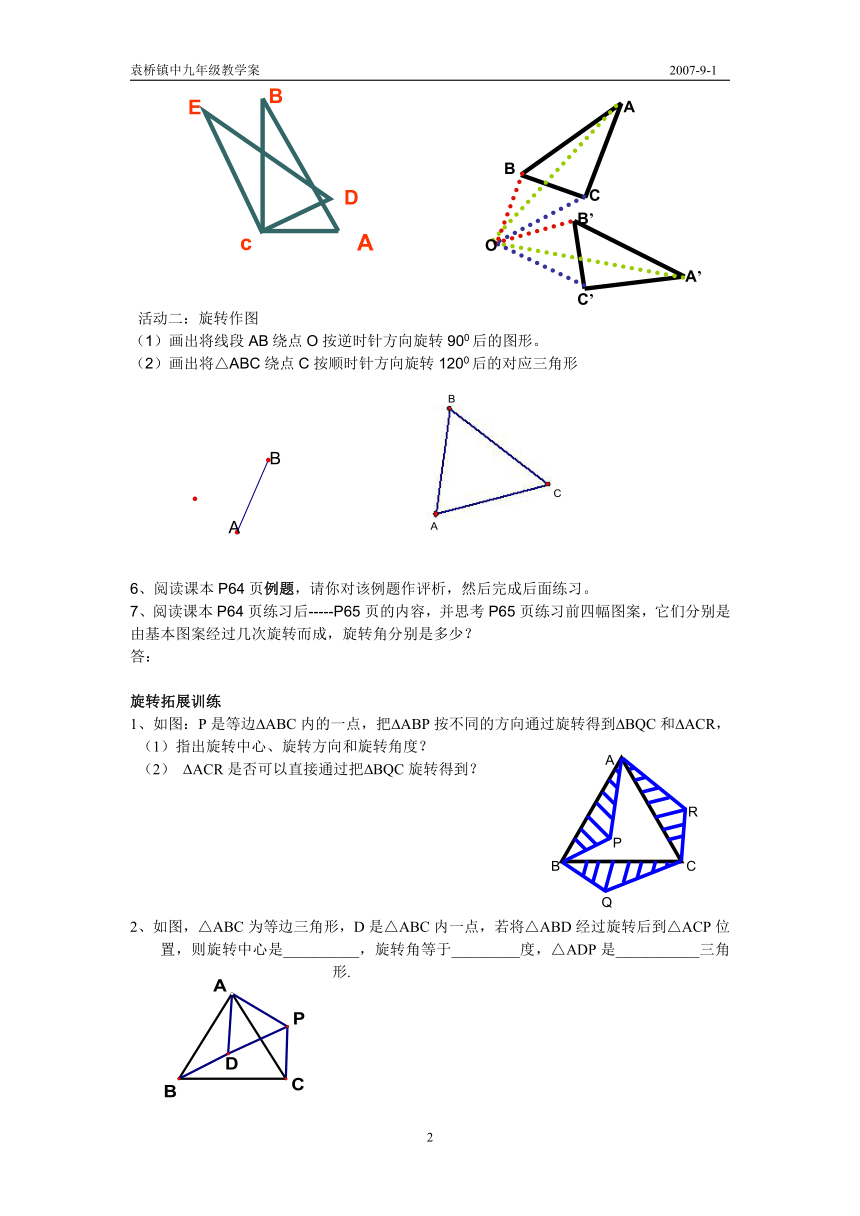
活动一:(1)将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.度量∠ACD与∠BCE的度数,线段AC与DC,BC与EC的长度.你发现了什么?
(2)将△ABC绕点O按顺时针方向旋转到△A ' B ' C '的位置,度量∠AOA' 、∠BOB' 、∠COC'的度数,线段AO与AO',BO与BO',CO与CO'的长度.你发现了什么
猜想归纳:旋转的性质:
活动二:旋转作图
(1)画出将线段AB绕点O按逆时针方向旋转900后的图形。
(2)画出将△ABC绕点C按顺时针方向旋转1200后的对应三角形
6、阅读课本P64页例题,请你对该例题作评析,然后完成后面练习。
7、阅读课本P64页练习后-----P65页的内容,并思考P65页练习前四幅图案,它们分别是由基本图案经过几次旋转而成,旋转角分别是多少?
答:
旋转拓展训练
1、如图:P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把BQC旋转得到?
2、如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
3、在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度.
4、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.
5、已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
6、 如图,在直角三角形ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A’B’C的位置,其中A’、B’分别是A、B的对应点,且点B在斜边A’B’上,直角边CA’交AB于点D,则∠DCA的度数_____________。
.
7、如图,正方形ABCD的边长为1,P为AB上的点,
Q为AD上的点,且△APQ的周长为2,
则∠PCQ=_______
8、已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,正方形的边长为4,求图中阴影部分的
D'
D
A'
A
B
O
B'
A
D
B
E
c
A’
C’
B’
A
C
B
O
D
B
C
P
R
Q
A
(第5题)
PAGE
4
23.1图形的旋转
一、教学目标
教学知识点:1.旋转的定义 2.旋转的基本性质.
能力训练要求:1.通过具体实例认识旋转,理解旋转的基本涵义;
2.通过具体实例认识旋转,知道旋转的性质;
3、经历对具有旋转特征的图形的观察、操作、画图等过程,掌握作图的技能。
二、教学过程:
1、阅读课本P62页“观察”或电脑演示:钟表指针的转动、汽车方向盘的转动、辘轳打水的情景). 问:(1)上面情景中的转动现象,有什么共同特征?
(2)钟表的指针、钟摆在转动过程中,其形状、大小、位置是否发生改变?汽车方向盘的转动呢?
2、归纳旋转的定义:
3、课本P63页练习:学生口答
4、随堂巩固:
(1)下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
(2) 香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,
它是由其中一瓣经过几次旋转得到的?
(3)如图,是△AOB绕点O按逆时针方向旋转450所得的。则点B的对应点是点_____。线段OB的对应线段是线段______。 线段AB的对应线段是线段____。∠A的对应角是______。∠B的对应角是______。旋转中心是点_____。旋转的角度是 ______ _
(4)如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
5、探究活动:(图形见右上)
活动一:(1)将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.度量∠ACD与∠BCE的度数,线段AC与DC,BC与EC的长度.你发现了什么?
(2)将△ABC绕点O按顺时针方向旋转到△A ' B ' C '的位置,度量∠AOA' 、∠BOB' 、∠COC'的度数,线段AO与AO',BO与BO',CO与CO'的长度.你发现了什么
猜想归纳:旋转的性质:
活动二:旋转作图
(1)画出将线段AB绕点O按逆时针方向旋转900后的图形。
(2)画出将△ABC绕点C按顺时针方向旋转1200后的对应三角形
6、阅读课本P64页例题,请你对该例题作评析,然后完成后面练习。
7、阅读课本P64页练习后-----P65页的内容,并思考P65页练习前四幅图案,它们分别是由基本图案经过几次旋转而成,旋转角分别是多少?
答:
旋转拓展训练
1、如图:P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把BQC旋转得到?
2、如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
3、在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度.
4、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.
5、已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
6、 如图,在直角三角形ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A’B’C的位置,其中A’、B’分别是A、B的对应点,且点B在斜边A’B’上,直角边CA’交AB于点D,则∠DCA的度数_____________。
.
7、如图,正方形ABCD的边长为1,P为AB上的点,
Q为AD上的点,且△APQ的周长为2,
则∠PCQ=_______
8、已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,正方形的边长为4,求图中阴影部分的
D'
D
A'
A
B
O
B'
A
D
B
E
c
A’
C’
B’
A
C
B
O
D
B
C
P
R
Q
A
(第5题)
PAGE
4
同课章节目录
