第三章圆压轴证明题训练二 无答案 2022—2023学年北师大版数学九年级下册
文档属性
| 名称 | 第三章圆压轴证明题训练二 无答案 2022—2023学年北师大版数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 312.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 21:19:47 | ||
图片预览

文档简介
北师大版数学九年级下册
第三章圆压轴证明题训练二
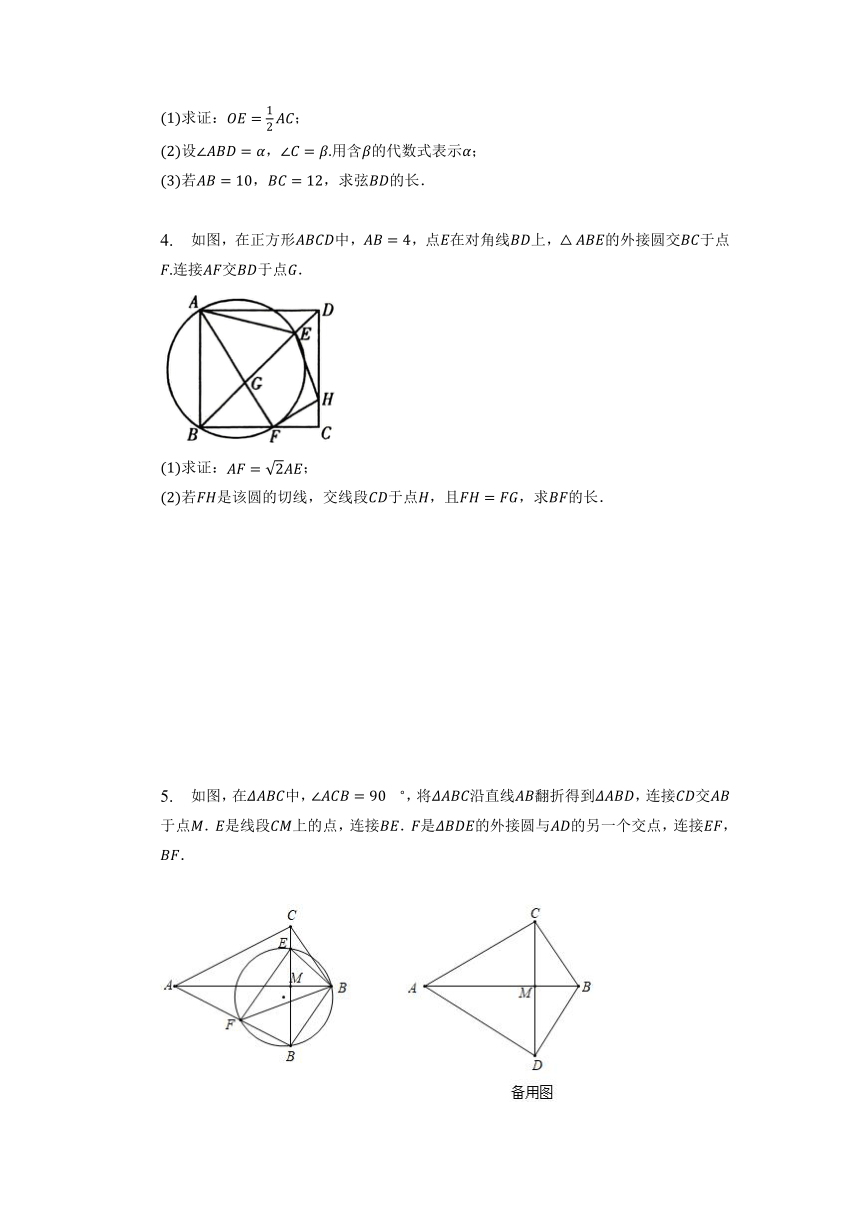
1. 已知如图,以的边为直径作交斜边于点,连接并延长交的延长线于点,作交于点,连接.
求证:
求证:是的切线;
若的半径为,,求的长.
2. 已知是的直径,,点在的半径上运动,,垂足为,,为的切线,切点为.
如上图,当点运动到点时,求的长;
如上图,当点运动到点时,连接、,求证:;
如上图,设,,求与的函数关系式.
3. 如图,以的一边为直径的半圆与边,分别交于点,,且平分.
求证:;
设,用含的代数式表示;
若,,求弦的长.
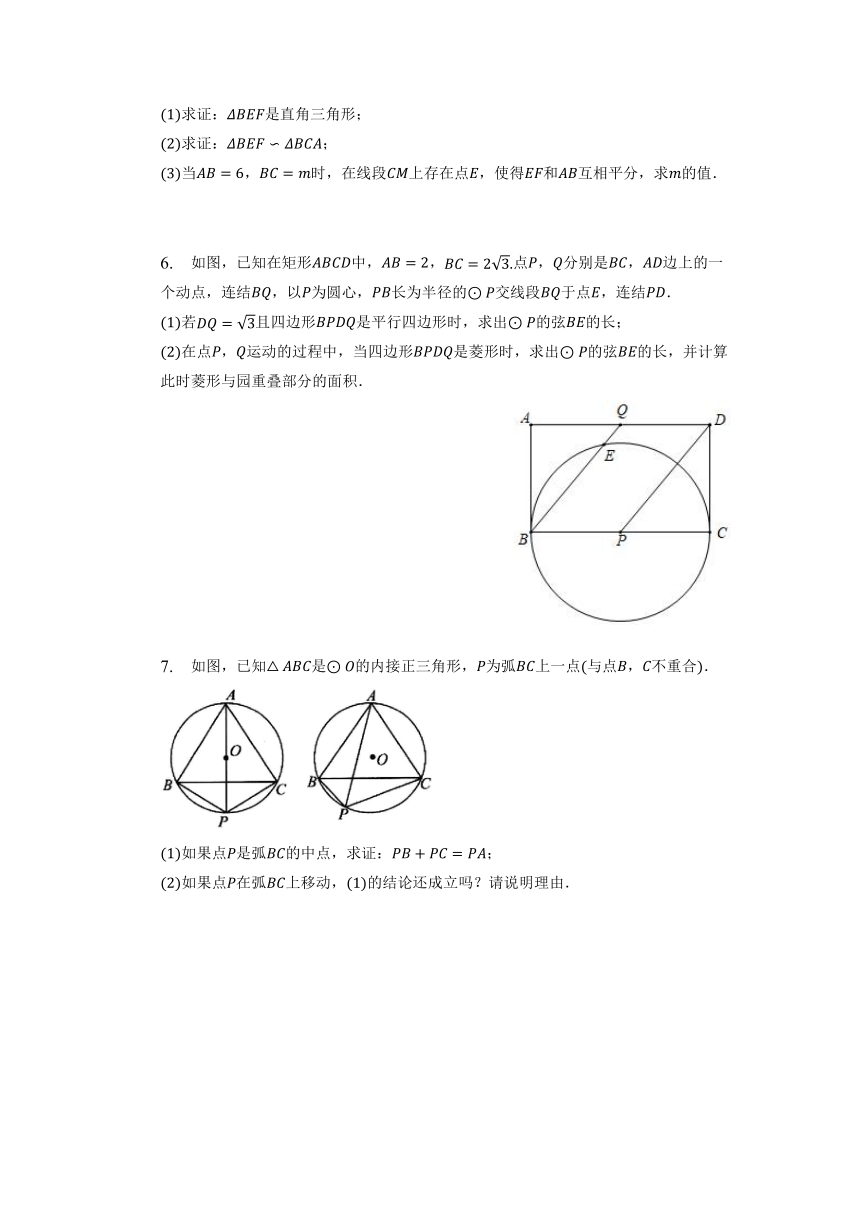
4. 如图,在正方形中,,点在对角线上,的外接圆交于点连接交于点.
求证:;
若是该圆的切线,交线段于点,且,求的长.
5. 如图,在中,,将沿直线翻折得到,连接交于点.是线段上的点,连接.是的外接圆与的另一个交点,连接,.
求证:是直角三角形;
求证:;
当,时,在线段上存在点,使得和互相平分,求的值.
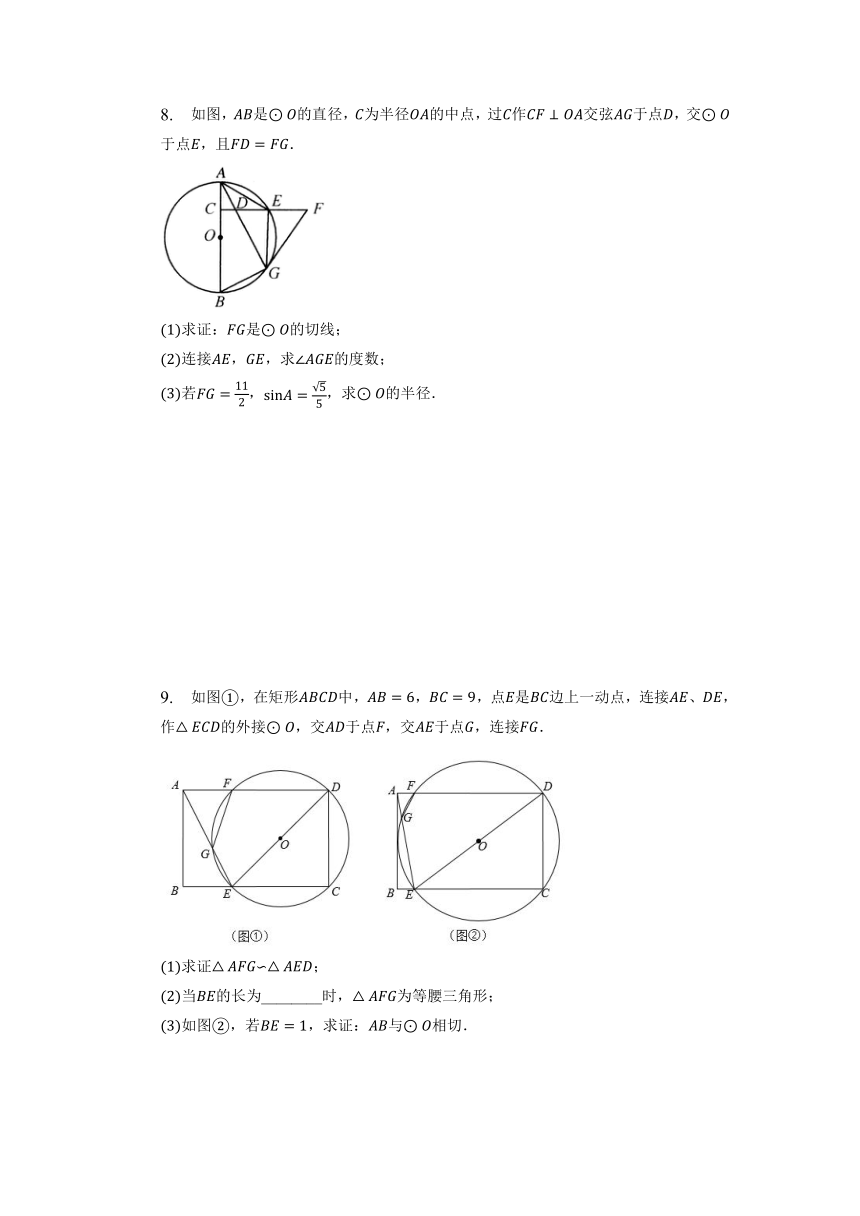
6. 如图,已知在矩形中,,点,分别是,边上的一个动点,连结,以为圆心,长为半径的交线段于点,连结.
若且四边形是平行四边形时,求出的弦的长;
在点,运动的过程中,当四边形是菱形时,求出的弦的长,并计算此时菱形与园重叠部分的面积.
7. 如图,已知是的内接正三角形,为弧上一点与点,不重合.
如果点是弧的中点,求证:;
如果点在弧上移动,的结论还成立吗?请说明理由.
8. 如图,是的直径,为半径的中点,过作交弦于点,交于点,且.
求证:是的切线;
连接,,求的度数;
若,,求的半径.
9. 如图,在矩形中,,,点是边上一动点,连接、,作的外接,交于点,交于点,连接.
求证∽;
当的长为________时,为等腰三角形;
如图,若,求证:与相切.
10. 如图,是的直径,,为上位于异侧的两点,连结并延长至点,使得,连结交于点,连接,,.
若,求的度数.
若,,是的中点,求的长.
11. 已知为的直径,于,且,为半圆上的一点,连接并延长交半圆的切线于.
如图,若,求证:是的切线;
如图,若点在上,且,求的值.
12. 如图,为的直径,点、都在上,且平分,交于点.
求证:;
若,,求的半径;
作于点,试探究线段、、之间的数量关系,并说明理由.
13. 如图,是的外接圆,是直径,是中点,直线与相交于,两点,是外一点,在直线上,连接,,,且满足.
求证:是的切线;
证明:;
若,,求的长.
14. 如图,是的外接圆,为直径,是上一点,且弧弧,交的延长线于点.
求证:;
求证:是的切线;
若,,求的半径长.
15. 如图,中,,,,,且,点从点出发,以的速度沿射线移动,以为直径作,交射线于点,连结,,过点作交于点,连接.
求证:∽;
设点的运动时间为,当与射线相切时,求的值;
当与射线相切时,点停止移动,在点移动的过程中,求点移动的路线长.
16. 如图,已知为的直径,,点和点是上关于直线对称的两个点,连接、,且,直线和直线相交于点,过点作直线与线段的延长线相交于点,与直线相交于点,且.
求证:直线为的切线;
若点为线段上一点,连接,满足,
∽;
求的最大值.
第三章圆压轴证明题训练二
1. 已知如图,以的边为直径作交斜边于点,连接并延长交的延长线于点,作交于点,连接.
求证:
求证:是的切线;
若的半径为,,求的长.
2. 已知是的直径,,点在的半径上运动,,垂足为,,为的切线,切点为.
如上图,当点运动到点时,求的长;
如上图,当点运动到点时,连接、,求证:;
如上图,设,,求与的函数关系式.
3. 如图,以的一边为直径的半圆与边,分别交于点,,且平分.
求证:;
设,用含的代数式表示;
若,,求弦的长.
4. 如图,在正方形中,,点在对角线上,的外接圆交于点连接交于点.
求证:;
若是该圆的切线,交线段于点,且,求的长.
5. 如图,在中,,将沿直线翻折得到,连接交于点.是线段上的点,连接.是的外接圆与的另一个交点,连接,.
求证:是直角三角形;
求证:;
当,时,在线段上存在点,使得和互相平分,求的值.
6. 如图,已知在矩形中,,点,分别是,边上的一个动点,连结,以为圆心,长为半径的交线段于点,连结.
若且四边形是平行四边形时,求出的弦的长;
在点,运动的过程中,当四边形是菱形时,求出的弦的长,并计算此时菱形与园重叠部分的面积.
7. 如图,已知是的内接正三角形,为弧上一点与点,不重合.
如果点是弧的中点,求证:;
如果点在弧上移动,的结论还成立吗?请说明理由.
8. 如图,是的直径,为半径的中点,过作交弦于点,交于点,且.
求证:是的切线;
连接,,求的度数;
若,,求的半径.
9. 如图,在矩形中,,,点是边上一动点,连接、,作的外接,交于点,交于点,连接.
求证∽;
当的长为________时,为等腰三角形;
如图,若,求证:与相切.
10. 如图,是的直径,,为上位于异侧的两点,连结并延长至点,使得,连结交于点,连接,,.
若,求的度数.
若,,是的中点,求的长.
11. 已知为的直径,于,且,为半圆上的一点,连接并延长交半圆的切线于.
如图,若,求证:是的切线;
如图,若点在上,且,求的值.
12. 如图,为的直径,点、都在上,且平分,交于点.
求证:;
若,,求的半径;
作于点,试探究线段、、之间的数量关系,并说明理由.
13. 如图,是的外接圆,是直径,是中点,直线与相交于,两点,是外一点,在直线上,连接,,,且满足.
求证:是的切线;
证明:;
若,,求的长.
14. 如图,是的外接圆,为直径,是上一点,且弧弧,交的延长线于点.
求证:;
求证:是的切线;
若,,求的半径长.
15. 如图,中,,,,,且,点从点出发,以的速度沿射线移动,以为直径作,交射线于点,连结,,过点作交于点,连接.
求证:∽;
设点的运动时间为,当与射线相切时,求的值;
当与射线相切时,点停止移动,在点移动的过程中,求点移动的路线长.
16. 如图,已知为的直径,,点和点是上关于直线对称的两个点,连接、,且,直线和直线相交于点,过点作直线与线段的延长线相交于点,与直线相交于点,且.
求证:直线为的切线;
若点为线段上一点,连接,满足,
∽;
求的最大值.
