【专题1】函数性质的综合应用 2023届高考数学三轮冲刺专题复习 课件(共66张PPT)
文档属性
| 名称 | 【专题1】函数性质的综合应用 2023届高考数学三轮冲刺专题复习 课件(共66张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 11:35:35 | ||
图片预览











文档简介
(共66张PPT)
【专题1】 函数性质的综合应用
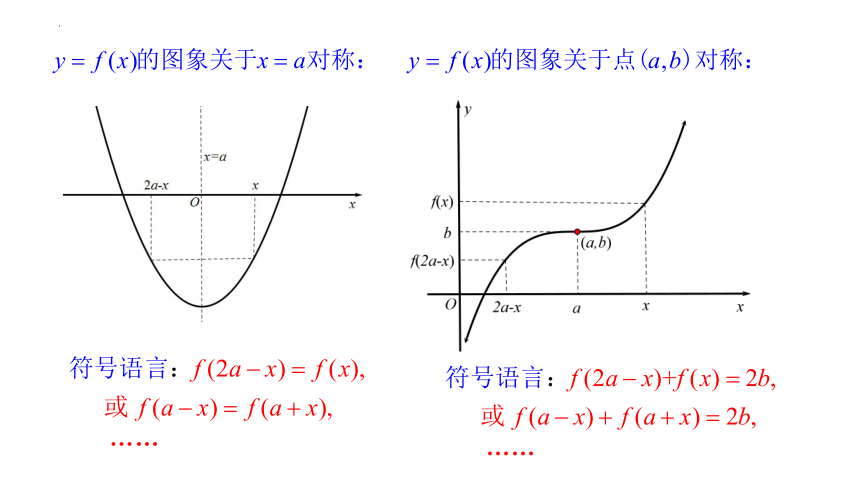
【例】如何理解函数奇偶性概念?
偶函数的图形语言:
奇函数的图形语言:
【专题3】 二项分布与函数、数列
【专题4】向量式转化为数量式的方法
解法五:奔驰定理
【专题6】与动点有关的问题
【专题7】证明直线过定点问题的方法
y
-x
X
0
X
1X=0
1
1
2-x
1
X
o'
x
sin a
=7,
cos a
[解析]由题意可得
sin2 a +cos2 a =1,
人a∈[0,r],
解得csa=V2
0
所以sma=7V2
10
3
于是cos(a+45)=cos a cos45°-sin a sin45°=-
解法二:建立如图所示的直角坐标系.+
寸是o=as9.00-59.C-(50
[2m+2n=N5,
由OC=mOA十nOB,得
10
2
2
(1
m+
2
10
m=
解得
8
从而m+n=3.
14
7=
8
解法四:利用三角形重心的性质
设OA=OA,0B=20B,0C=40C,则0A+OB+0C=0.
所以0是A4BC的重心,于是S4os=SA4oC=SBoc=S。·
由01=01,0B=20丽.知S03-}s
7
+·Q一三W08 VOLDOPVCL&0FV1=aol208Vm1=w0r由EH
7
从而
SMBC
故选A.
2
B
2
A
5
A
-2
-4十
2
1.
0.5
B
-0.5
P
-1.5
C
V2x
X
A
B
3
C
2
A
2
B
2
3
C
1
2
A
2
B
1
个y
1
O
e
1-b
1
1
1
1
X
一
a
b
a
2
个y
O
e
1-b
1
1
1
1
x
一
1
b
a
2
【专题1】 函数性质的综合应用
【例】如何理解函数奇偶性概念?
偶函数的图形语言:
奇函数的图形语言:
【专题3】 二项分布与函数、数列
【专题4】向量式转化为数量式的方法
解法五:奔驰定理
【专题6】与动点有关的问题
【专题7】证明直线过定点问题的方法
y
-x
X
0
X
1X=0
1
1
2-x
1
X
o'
x
sin a
=7,
cos a
[解析]由题意可得
sin2 a +cos2 a =1,
人a∈[0,r],
解得csa=V2
0
所以sma=7V2
10
3
于是cos(a+45)=cos a cos45°-sin a sin45°=-
解法二:建立如图所示的直角坐标系.+
寸是o=as9.00-59.C-(50
[2m+2n=N5,
由OC=mOA十nOB,得
10
2
2
(1
m+
2
10
m=
解得
8
从而m+n=3.
14
7=
8
解法四:利用三角形重心的性质
设OA=OA,0B=20B,0C=40C,则0A+OB+0C=0.
所以0是A4BC的重心,于是S4os=SA4oC=SBoc=S。·
由01=01,0B=20丽.知S03-}s
7
+·Q一三W08 VOLDOPVCL&0FV1=aol208Vm1=w0r由EH
7
从而
SMBC
故选A.
2
B
2
A
5
A
-2
-4十
2
1.
0.5
B
-0.5
P
-1.5
C
V2x
X
A
B
3
C
2
A
2
B
2
3
C
1
2
A
2
B
1
个y
1
O
e
1-b
1
1
1
1
X
一
a
b
a
2
个y
O
e
1-b
1
1
1
1
x
一
1
b
a
2
同课章节目录
