18.2.2 菱形同步测试题(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
菱形的性质同步练习
一、单选题:
1.下面性质中,菱形不一定具备的是( )
A. 四条边都相等 B. 每一条对角线平分一组对角 C. 邻角互补 D. 对角线相等
2.下列性质中,菱形对角线不具有的是( )
A. 对角线互相垂直 B. 对角线所在直线是对称轴 C. 对角线相等 D. 对角线互相平分
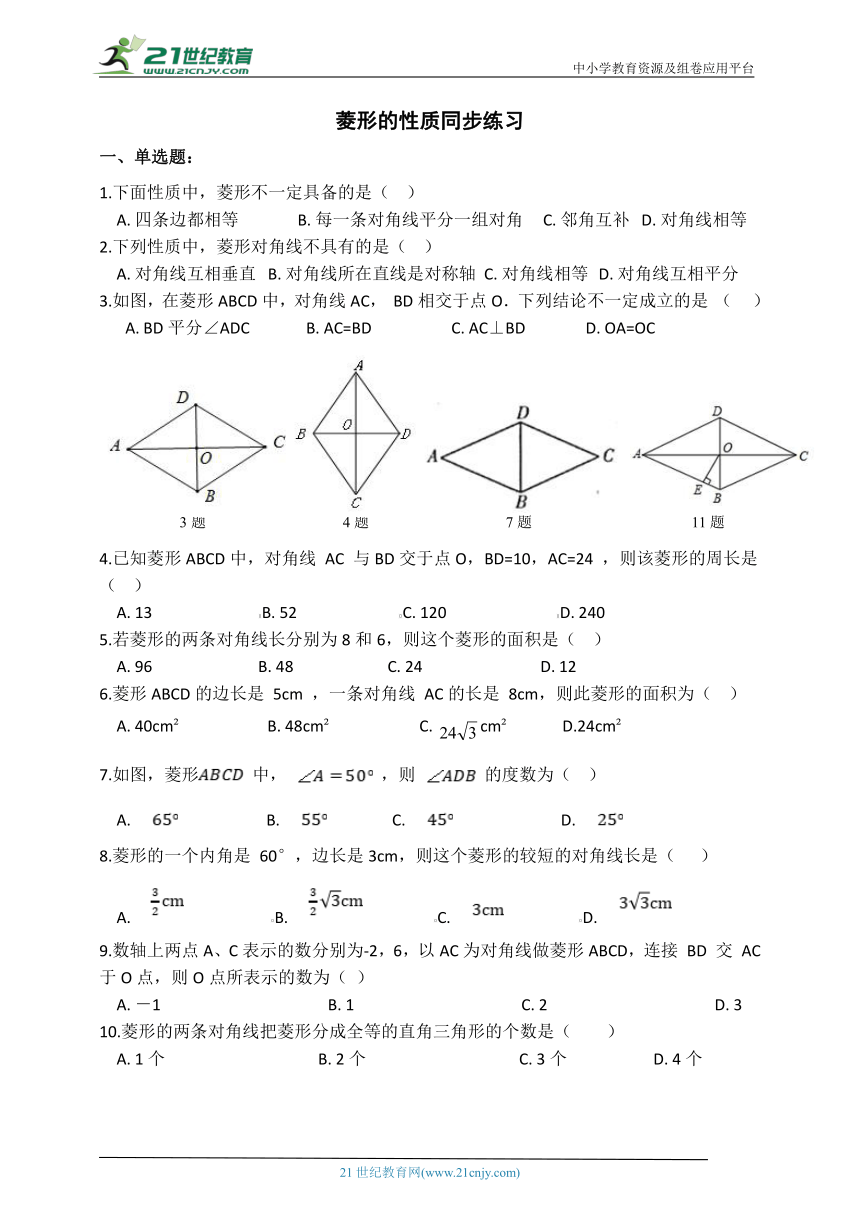
3.如图,在菱形ABCD中,对角线AC, BD相交于点O.下列结论不一定成立的是 ( )
A. BD平分∠ADC B. AC=BD C. AC⊥BD D. OA=OC
4.已知菱形ABCD中,对角线 AC 与BD交于点O,BD=10,AC=24 ,则该菱形的周长是( )
A. 13 B. 52 C. 120 D. 240
5.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A. 96 B. 48 C. 24 D. 12
6.菱形ABCD的边长是 5cm ,一条对角线 AC的长是 8cm,则此菱形的面积为( )
A. 40cm B. 48cm C. cm D.24cm
7.如图,菱形 中, ,则 的度数为( )
A. B. C. D.
8.菱形的一个内角是 60°,边长是3cm,则这个菱形的较短的对角线长是( )
A. B. C. D.
9.数轴上两点A、C表示的数分别为-2,6,以AC为对角线做菱形ABCD,连接 BD 交 AC 于O点,则O点所表示的数为( )
A. -1 B. 1 C. 2 D. 3
10.菱形的两条对角线把菱形分成全等的直角三角形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
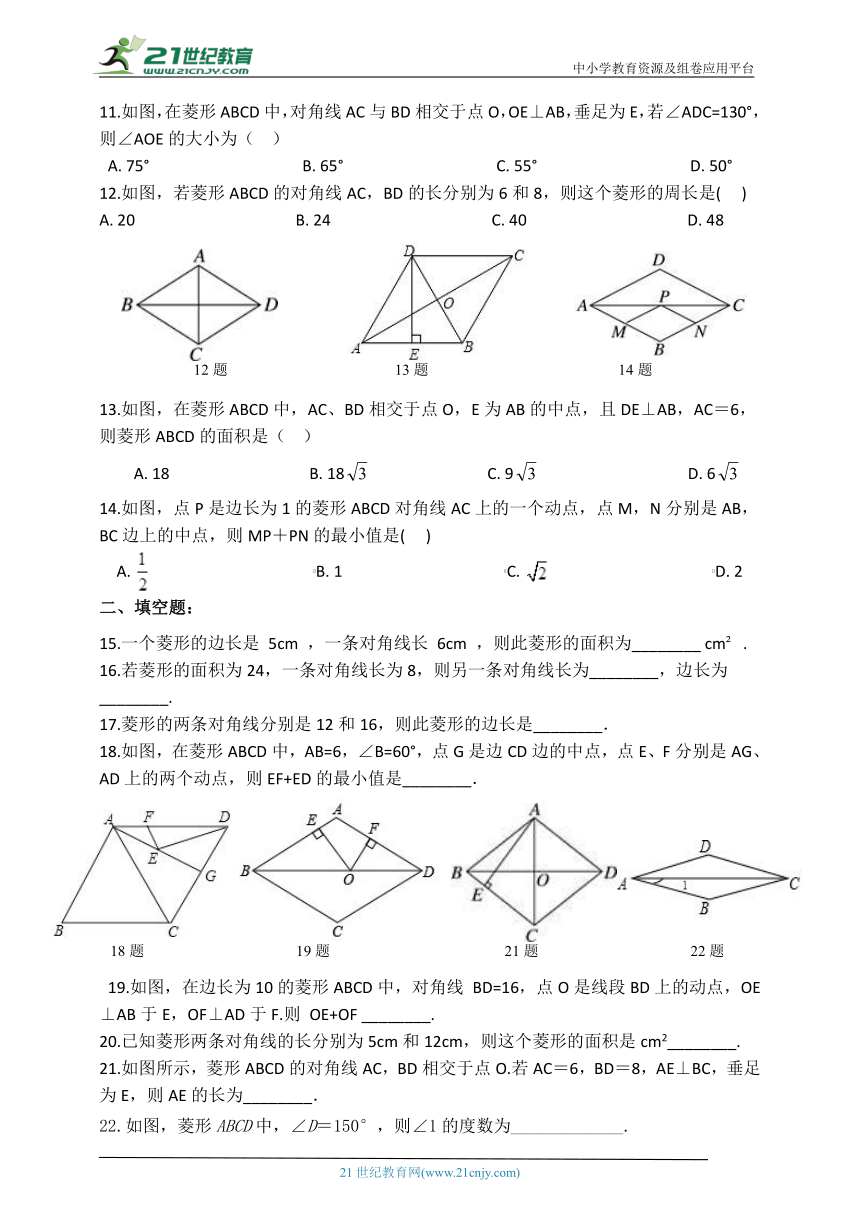
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A. 75° B. 65° C. 55° D. 50°
12.如图,若菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( ) A. 20 B. 24 C. 40 D. 48
13.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A. 18 B. 18 C. 9 D. 6
14.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A. B. 1 C. D. 2
二、填空题:
15.一个菱形的边长是 5cm ,一条对角线长 6cm ,则此菱形的面积为________ cm .
16.若菱形的面积为24,一条对角线长为8,则另一条对角线长为________,边长为________.
17.菱形的两条对角线分别是12和16,则此菱形的边长是________.
18.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是________.
19.如图,在边长为10的菱形ABCD中,对角线 BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则 OE+OF ________.
20.已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是cm2________.
21.如图所示,菱形ABCD的对角线AC,BD相交于点O.若AC=6,BD=8,AE⊥BC,垂足为E,则AE的长为________.
22.如图,菱形ABCD中,∠D=150°,则∠1的度数为_____________.
三、解答题:
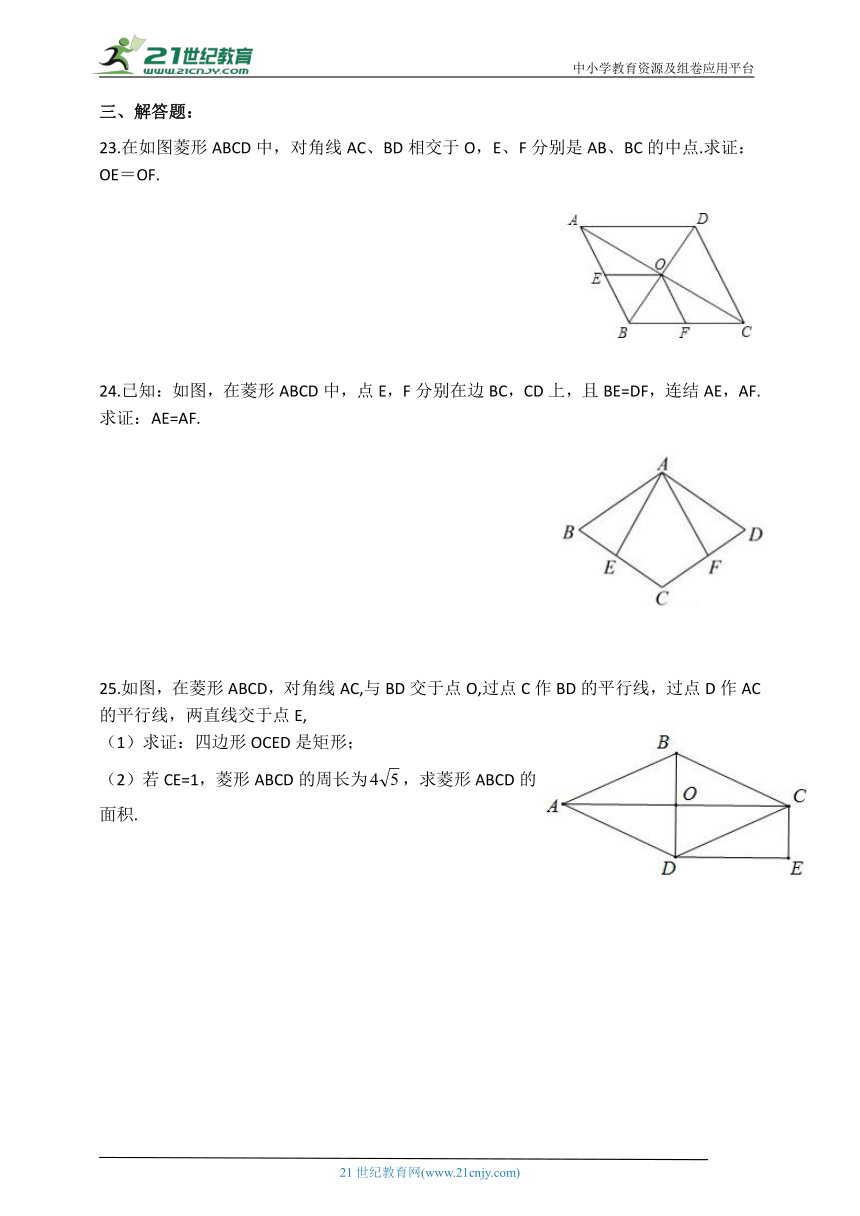
23.在如图菱形ABCD中,对角线AC、BD相交于O,E、F分别是AB、BC的中点.求证:OE=OF.
24.已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
25.如图,在菱形ABCD,对角线AC,与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线交于点E,
(1)求证:四边形OCED是矩形;
(2)若CE=1,菱形ABCD的周长为,求菱形ABCD的面积.
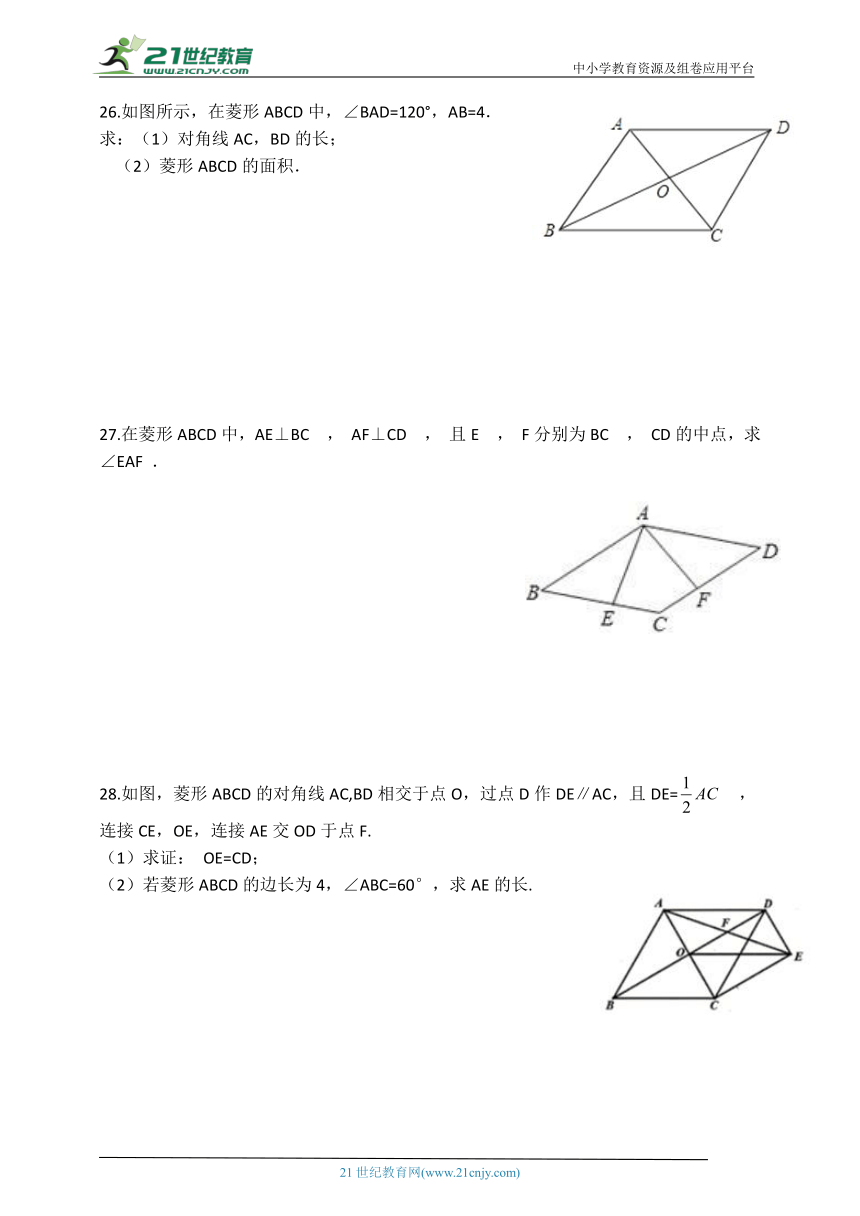
26.如图所示,在菱形ABCD中,∠BAD=120°,AB=4.
求:(1)对角线AC,BD的长;
(2)菱形ABCD的面积.
27.在菱形ABCD中,AE⊥BC , AF⊥CD , 且E , F分别为BC , CD的中点,求∠EAF .
28.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC,且DE= ,连接CE,OE,连接AE交OD于点F.
(1)求证: OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
参考答案
选择题
1.D
2.B
3.C
4.B
5.C
6.D
7.A
8.C
9.C
10.D
11.B
12.A
13.D
14.B
二、填空题
15、24
16、6;5
17、10
18、3
19、9.6
20、30
21、
22、15°
三、解答题
23.解:∵AC⊥BD,∴△AOB、△BOC为直角三角形,
∵E、F分别是AB、BC的中点,
∴OE= ,OF= ,
∵AB=BC,
∴OE=OF.
24.证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=DF
∴△ABE≌△ADF.
∴AE=CF
25.(1)证明:因为四边形ABCD是菱形,
所以 ,
,
,
所以四边形OCED是平行四边形,
,
∴四边形OCED是矩形;
(2)解:由(1)知,四边形OCED是矩形,
则CE=OD=1,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,
∵菱形ABCD的周长为 ,
,
,
,
∴菱形ABCD的面积为: .
26.(1)证明:在菱形ABCD中
OC= AC,AC⊥BD,
∵DE= AC,
∴DE=OC,
∵DE∥OC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴□OCED是矩形,
∴OE=CD.
(2)解:在菱形ABCD中,AB=BC=4,
∵∠ABC=60 ,
∴△ABC是等边三角形,
∴AC=AB=4,OA= AC=2,
在Rt△AOB中, ,
∵四边形OCED是矩形,
∴OD=CE=OB= ,
在Rt△ACE中, .
解:∵AE⊥BC , AF⊥CD
∴∠AFC+∠AEC=180°
∴∠C+∠EAF=180°
又∵∠B+∠C=180°
∴∠EAF=∠B
又∵BE= BC , AB=BC
∴BE= AB
∴∠BAE=30°
∴∠B=60°
∴∠EAF=60°.
28.解:
(2)∵菱形ABCD
∴AB=BC,OA=,OB=OD,∠AOB=90°
∵∠ABC=60°
∴△ABC是等边三角形
∴AC=AB=4
∴OA==2
在Rt△AOB中,由勾股定理得,OB=
∴OB=OD=
∵矩形OCED
∴ ∠ACE=90°OD=CE=
在Rt△ACE中,由勾股定理得,AE=
3题 4题 7题 11题
12题 13题 14题
18题 19题 21题 22题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
菱形的性质同步练习
一、单选题:
1.下面性质中,菱形不一定具备的是( )
A. 四条边都相等 B. 每一条对角线平分一组对角 C. 邻角互补 D. 对角线相等
2.下列性质中,菱形对角线不具有的是( )
A. 对角线互相垂直 B. 对角线所在直线是对称轴 C. 对角线相等 D. 对角线互相平分
3.如图,在菱形ABCD中,对角线AC, BD相交于点O.下列结论不一定成立的是 ( )
A. BD平分∠ADC B. AC=BD C. AC⊥BD D. OA=OC
4.已知菱形ABCD中,对角线 AC 与BD交于点O,BD=10,AC=24 ,则该菱形的周长是( )
A. 13 B. 52 C. 120 D. 240
5.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A. 96 B. 48 C. 24 D. 12
6.菱形ABCD的边长是 5cm ,一条对角线 AC的长是 8cm,则此菱形的面积为( )
A. 40cm B. 48cm C. cm D.24cm
7.如图,菱形 中, ,则 的度数为( )
A. B. C. D.
8.菱形的一个内角是 60°,边长是3cm,则这个菱形的较短的对角线长是( )
A. B. C. D.
9.数轴上两点A、C表示的数分别为-2,6,以AC为对角线做菱形ABCD,连接 BD 交 AC 于O点,则O点所表示的数为( )
A. -1 B. 1 C. 2 D. 3
10.菱形的两条对角线把菱形分成全等的直角三角形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A. 75° B. 65° C. 55° D. 50°
12.如图,若菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( ) A. 20 B. 24 C. 40 D. 48
13.如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A. 18 B. 18 C. 9 D. 6
14.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A. B. 1 C. D. 2
二、填空题:
15.一个菱形的边长是 5cm ,一条对角线长 6cm ,则此菱形的面积为________ cm .
16.若菱形的面积为24,一条对角线长为8,则另一条对角线长为________,边长为________.
17.菱形的两条对角线分别是12和16,则此菱形的边长是________.
18.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是________.
19.如图,在边长为10的菱形ABCD中,对角线 BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则 OE+OF ________.
20.已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是cm2________.
21.如图所示,菱形ABCD的对角线AC,BD相交于点O.若AC=6,BD=8,AE⊥BC,垂足为E,则AE的长为________.
22.如图,菱形ABCD中,∠D=150°,则∠1的度数为_____________.
三、解答题:
23.在如图菱形ABCD中,对角线AC、BD相交于O,E、F分别是AB、BC的中点.求证:OE=OF.
24.已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
25.如图,在菱形ABCD,对角线AC,与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线交于点E,
(1)求证:四边形OCED是矩形;
(2)若CE=1,菱形ABCD的周长为,求菱形ABCD的面积.
26.如图所示,在菱形ABCD中,∠BAD=120°,AB=4.
求:(1)对角线AC,BD的长;
(2)菱形ABCD的面积.
27.在菱形ABCD中,AE⊥BC , AF⊥CD , 且E , F分别为BC , CD的中点,求∠EAF .
28.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC,且DE= ,连接CE,OE,连接AE交OD于点F.
(1)求证: OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
参考答案
选择题
1.D
2.B
3.C
4.B
5.C
6.D
7.A
8.C
9.C
10.D
11.B
12.A
13.D
14.B
二、填空题
15、24
16、6;5
17、10
18、3
19、9.6
20、30
21、
22、15°
三、解答题
23.解:∵AC⊥BD,∴△AOB、△BOC为直角三角形,
∵E、F分别是AB、BC的中点,
∴OE= ,OF= ,
∵AB=BC,
∴OE=OF.
24.证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=DF
∴△ABE≌△ADF.
∴AE=CF
25.(1)证明:因为四边形ABCD是菱形,
所以 ,
,
,
所以四边形OCED是平行四边形,
,
∴四边形OCED是矩形;
(2)解:由(1)知,四边形OCED是矩形,
则CE=OD=1,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,
∵菱形ABCD的周长为 ,
,
,
,
∴菱形ABCD的面积为: .
26.(1)证明:在菱形ABCD中
OC= AC,AC⊥BD,
∵DE= AC,
∴DE=OC,
∵DE∥OC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴□OCED是矩形,
∴OE=CD.
(2)解:在菱形ABCD中,AB=BC=4,
∵∠ABC=60 ,
∴△ABC是等边三角形,
∴AC=AB=4,OA= AC=2,
在Rt△AOB中, ,
∵四边形OCED是矩形,
∴OD=CE=OB= ,
在Rt△ACE中, .
解:∵AE⊥BC , AF⊥CD
∴∠AFC+∠AEC=180°
∴∠C+∠EAF=180°
又∵∠B+∠C=180°
∴∠EAF=∠B
又∵BE= BC , AB=BC
∴BE= AB
∴∠BAE=30°
∴∠B=60°
∴∠EAF=60°.
28.解:
(2)∵菱形ABCD
∴AB=BC,OA=,OB=OD,∠AOB=90°
∵∠ABC=60°
∴△ABC是等边三角形
∴AC=AB=4
∴OA==2
在Rt△AOB中,由勾股定理得,OB=
∴OB=OD=
∵矩形OCED
∴ ∠ACE=90°OD=CE=
在Rt△ACE中,由勾股定理得,AE=
3题 4题 7题 11题
12题 13题 14题
18题 19题 21题 22题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
