江苏省淮安市2022-2023学年人教版九年级下学期期中数学试卷 无答案
文档属性
| 名称 | 江苏省淮安市2022-2023学年人教版九年级下学期期中数学试卷 无答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 259.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 00:00:00 | ||
图片预览


文档简介
淮安市2022-2023九年级下学期期中数学试卷
(时间:120分钟,总分:150分)
选择题(每小题3分,共24分)
1.下列四个实数中,是无理数的为( ▲ )
A. B. C. D.
2.运河三千里,最美在淮安,京杭大运河全长约1790000米,数据1790000用科学记数法表示为 ( ▲ )
A.0.179×107 B.17.9×105 C.1.79×106 D.179×103
3.计算x3÷x2的结果是 ( ▲ )
A.x B.x2 C.x3 D.x5
4.下列几何体中,主视图为三角形的是( ▲ )
B. C. D.
5.实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( ▲ )
a<﹣2 B.a+b>0 C.a 2<b2 D.﹣a>b
6.如右图,已知AB是圆O的直径,点C,D在圆O上,且∠ABC=32°,
则∠BDC度数为( ▲ )
A. 58° B.60° C. 62° D. 64°
7.某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:则关于这组数据的结论正确的是( ▲ )
一分钟跳绳个数(个) 145 170 165 150
学生人数(名) 1 2 5 2
A.中位数是167.5 B.平均数是160 C.众数是165 D.方差是2
8.如图,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为 ( ▲ )
B.
D.
填空题(每小题3分,共24分)
9.分解因式:x2﹣4= ▲ .
10.分式的值为0,则x的值是 ▲
11.若关于x的一元二次方程x2+x+m=0有两个相等的实数根,则实数m的值为 ▲
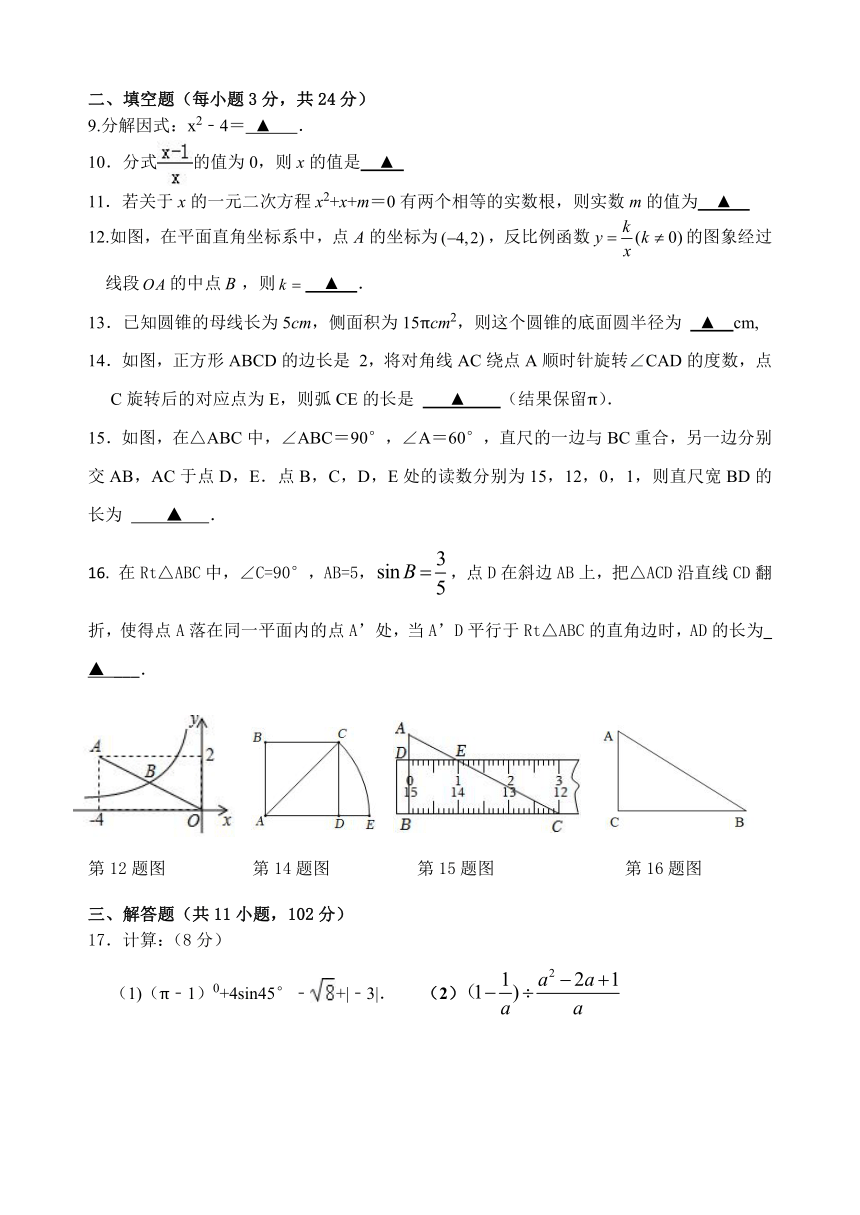
12.如图,在平面直角坐标系中,点的坐标为,反比例函数的图象经过线段的中点,则 ▲ .
13.已知圆锥的母线长为5cm,侧面积为15πcm2,则这个圆锥的底面圆半径为 ▲ cm,
14.如图,正方形ABCD的边长是 2,将对角线AC绕点A顺时针旋转∠CAD的度数,点C旋转后的对应点为E,则弧CE的长是 ▲ (结果保留π).
15.如图,在△ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为 ▲ .
16. 在Rt△ABC中,∠C=90°,AB=5,,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的点A’处,当A’D平行于Rt△ABC的直角边时,AD的长为_ ▲ ___.
第12题图 第14题图 第15题图 第16题图
解答题(共11小题,102分)
计算:(8分)
(1)(π﹣1)0+4sin45°﹣+|﹣3|. (2)
18.(6分)解不等式组:,并写出不等式组的整数解.
19.(8分)如图,在 ABCD中,点E、F分别是边AB、CD的中点.求证:AF=CE.
(8分)“五个一百工程”在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h 频数 频率
0<t≤0.5 24
0.5<t≤1 36 0.3
1<t≤1.5 0.4
1.5<t≤2 12 b
合计 a 1
根据以上信息,回答下列问题:
(1)表中a= ▲ ,b= ▲ ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生
每天课外阅读时间超过1小时的人数.
21.(8分)在5张相同的小纸条上,分别写有语句:①矩形;②菱形;③对角线相等;④四条边相等;⑤四个角为直角.将这5张小纸条做成5支签,①、②放在不透明的盒子A中搅匀,③、④、⑤放在不透明的盒子B中搅匀.
(1)从盒子A中任意抽出1支签,抽到①的概率是 ▲ ;
(2)先从盒子A中任意抽出1支签,再从盒子B中任意抽出1支签.求抽到的2张小纸条上的语句对图形的性质描述相符合的概率.
22.(10分)如图1是小明在健身器材上进行仰卧起坐锻炼时的情景,图2是小明锻炼时
上半身由ON位置运动到OM位置时的示意图,并且OM与地面CD垂直,已知AC=0.75米,
BD=0.25米, ,(参考数据 ).
AB的长为 ▲ 米;
若ON=0.7米,求M、N两点间的距离(精确到0.1米).
23.(6分)如图,已知∠α和线段a,请用直尺和圆规作△ABC, 使其满足:∠B=α,∠C=45°,
AB=a.(保留作图痕迹,不写作法)
α a
24.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
⑴求证:DF是⊙O的切线;
⑵若AE=4,,求DF的长.
25.(12分)如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事立刻按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图像信息解答下列问题:
(1)乙车的速度是 ▲ 千米/时,乙车行驶 ▲ 小时到达A地;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)求甲车出发多长时间两车相距60千米?
26.(12分)在Rt△ABC中,∠ACB=90°,AB=10,BC=6,将△ABC绕点B顺时针旋转得到△A’BC’,其中点A、C的对应点分别为点A’、C’.
如图1,当点A’落在AC的延长线上时,AA’的长为 ▲ ;
如图2,当点C’落在AB的延长线上时,连接CC’,交A’B于点M,
求线段CC’和BM的长;
(3)如图3,连接AA’,CC’,直线CC’与直线AA’交于点D,点E在边AC上,且AE= 5 ,连接DE,在旋转一周的过程中,DE的最小值为 ▲ .
(14分)如图1,在平面直角坐标系中,二次函数y=x2+bx+2的图象与x轴交于点
A(﹣1,0)和点B(4,0),与y轴交于点C,连接AC,BC.
(1)填空:= ,b= ,∠ACB= °;
(2)如图2,点P是线段BC上方抛物线上的一个动点.过点P作PQ∥CA交线段BC于点Q,设点P的横坐标为t,记.
①求f关于t的函数关系式;
②当t取m和m+1()时,试比较f的对应函数值f1和f2的大小.
(3)如图3,直线l:y=kx+3经过点A,点D是直线l上的动点,点E是x轴上的动点,点F是抛物线对称轴上的动点,当以A、D、E、F为顶点的四边形是菱形时,直接写出所有满足条件的点D的横坐标.
图1 图2 图3
(时间:120分钟,总分:150分)
选择题(每小题3分,共24分)
1.下列四个实数中,是无理数的为( ▲ )
A. B. C. D.
2.运河三千里,最美在淮安,京杭大运河全长约1790000米,数据1790000用科学记数法表示为 ( ▲ )
A.0.179×107 B.17.9×105 C.1.79×106 D.179×103
3.计算x3÷x2的结果是 ( ▲ )
A.x B.x2 C.x3 D.x5
4.下列几何体中,主视图为三角形的是( ▲ )
B. C. D.
5.实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( ▲ )
a<﹣2 B.a+b>0 C.a 2<b2 D.﹣a>b
6.如右图,已知AB是圆O的直径,点C,D在圆O上,且∠ABC=32°,
则∠BDC度数为( ▲ )
A. 58° B.60° C. 62° D. 64°
7.某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:则关于这组数据的结论正确的是( ▲ )
一分钟跳绳个数(个) 145 170 165 150
学生人数(名) 1 2 5 2
A.中位数是167.5 B.平均数是160 C.众数是165 D.方差是2
8.如图,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为 ( ▲ )
B.
D.
填空题(每小题3分,共24分)
9.分解因式:x2﹣4= ▲ .
10.分式的值为0,则x的值是 ▲
11.若关于x的一元二次方程x2+x+m=0有两个相等的实数根,则实数m的值为 ▲
12.如图,在平面直角坐标系中,点的坐标为,反比例函数的图象经过线段的中点,则 ▲ .
13.已知圆锥的母线长为5cm,侧面积为15πcm2,则这个圆锥的底面圆半径为 ▲ cm,
14.如图,正方形ABCD的边长是 2,将对角线AC绕点A顺时针旋转∠CAD的度数,点C旋转后的对应点为E,则弧CE的长是 ▲ (结果保留π).
15.如图,在△ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为 ▲ .
16. 在Rt△ABC中,∠C=90°,AB=5,,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的点A’处,当A’D平行于Rt△ABC的直角边时,AD的长为_ ▲ ___.
第12题图 第14题图 第15题图 第16题图
解答题(共11小题,102分)
计算:(8分)
(1)(π﹣1)0+4sin45°﹣+|﹣3|. (2)
18.(6分)解不等式组:,并写出不等式组的整数解.
19.(8分)如图,在 ABCD中,点E、F分别是边AB、CD的中点.求证:AF=CE.
(8分)“五个一百工程”在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h 频数 频率
0<t≤0.5 24
0.5<t≤1 36 0.3
1<t≤1.5 0.4
1.5<t≤2 12 b
合计 a 1
根据以上信息,回答下列问题:
(1)表中a= ▲ ,b= ▲ ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生
每天课外阅读时间超过1小时的人数.
21.(8分)在5张相同的小纸条上,分别写有语句:①矩形;②菱形;③对角线相等;④四条边相等;⑤四个角为直角.将这5张小纸条做成5支签,①、②放在不透明的盒子A中搅匀,③、④、⑤放在不透明的盒子B中搅匀.
(1)从盒子A中任意抽出1支签,抽到①的概率是 ▲ ;
(2)先从盒子A中任意抽出1支签,再从盒子B中任意抽出1支签.求抽到的2张小纸条上的语句对图形的性质描述相符合的概率.
22.(10分)如图1是小明在健身器材上进行仰卧起坐锻炼时的情景,图2是小明锻炼时
上半身由ON位置运动到OM位置时的示意图,并且OM与地面CD垂直,已知AC=0.75米,
BD=0.25米, ,(参考数据 ).
AB的长为 ▲ 米;
若ON=0.7米,求M、N两点间的距离(精确到0.1米).
23.(6分)如图,已知∠α和线段a,请用直尺和圆规作△ABC, 使其满足:∠B=α,∠C=45°,
AB=a.(保留作图痕迹,不写作法)
α a
24.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
⑴求证:DF是⊙O的切线;
⑵若AE=4,,求DF的长.
25.(12分)如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事立刻按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图像信息解答下列问题:
(1)乙车的速度是 ▲ 千米/时,乙车行驶 ▲ 小时到达A地;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)求甲车出发多长时间两车相距60千米?
26.(12分)在Rt△ABC中,∠ACB=90°,AB=10,BC=6,将△ABC绕点B顺时针旋转得到△A’BC’,其中点A、C的对应点分别为点A’、C’.
如图1,当点A’落在AC的延长线上时,AA’的长为 ▲ ;
如图2,当点C’落在AB的延长线上时,连接CC’,交A’B于点M,
求线段CC’和BM的长;
(3)如图3,连接AA’,CC’,直线CC’与直线AA’交于点D,点E在边AC上,且AE= 5 ,连接DE,在旋转一周的过程中,DE的最小值为 ▲ .
(14分)如图1,在平面直角坐标系中,二次函数y=x2+bx+2的图象与x轴交于点
A(﹣1,0)和点B(4,0),与y轴交于点C,连接AC,BC.
(1)填空:= ,b= ,∠ACB= °;
(2)如图2,点P是线段BC上方抛物线上的一个动点.过点P作PQ∥CA交线段BC于点Q,设点P的横坐标为t,记.
①求f关于t的函数关系式;
②当t取m和m+1()时,试比较f的对应函数值f1和f2的大小.
(3)如图3,直线l:y=kx+3经过点A,点D是直线l上的动点,点E是x轴上的动点,点F是抛物线对称轴上的动点,当以A、D、E、F为顶点的四边形是菱形时,直接写出所有满足条件的点D的横坐标.
图1 图2 图3
同课章节目录
