多项式与多项式相乘[上学期]
图片预览




文档简介
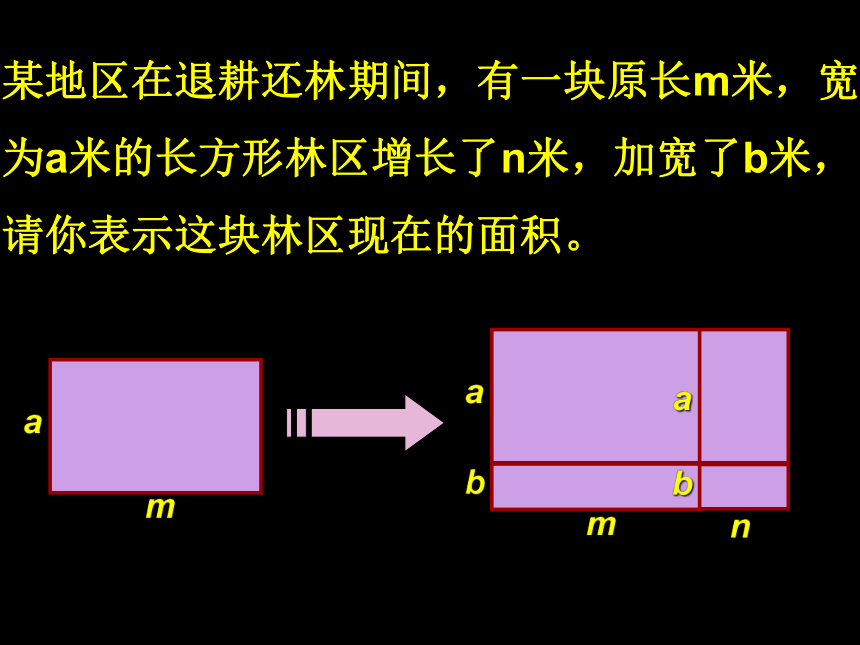
课件12张PPT。14.2节 整式的乘法 3. 多项式与多项式相乘回顾与思考② 再把所得的积相加。① 将单项式分别乘以多项式的各项,① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.某地区在退耕还林期间,有一块原长m米,宽
为a米的长方形林区增长了n米,加宽了b米,
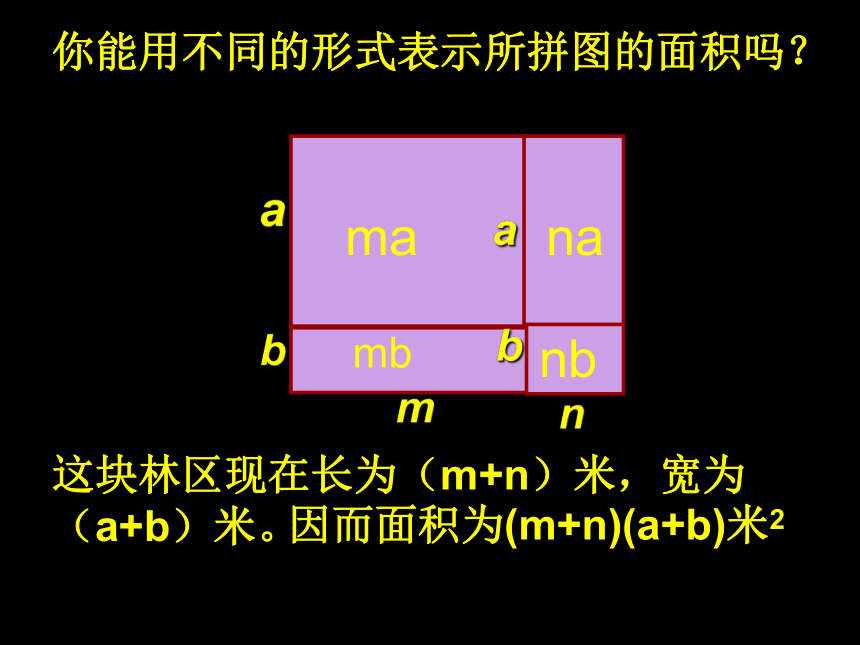
请你表示这块林区现在的面积。ma你能用不同的形式表示所拼图的面积吗?manambnb这块林区现在长为(m+n)米,宽为(a+b)米。因而面积为(m+n)(a+b)米2
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb(a+b)X=(a+b)(m+n)=ma+ mb+ na+ nb根据以上问题,讨论得知:如何进行多项式与多项式相乘的 运算 ?实际上,把(m+n)看成一个整体,有:(m+n)(a+b)=(m+n)a+(m+n)b=ma+ mb+ na+ nb(m+n)(a+b)=ma+ mb+ na+ nb先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。例题解析 【例4】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。?3x+2x=x2 -x-6 -2×3(2) (3x -1)(2x+1)=3x?2x+3x? 1-1?2 x?1=6x2+3x-2 x?1=6x2 +x?1. 【例5】计算: (1)(x?3y)(x+7y), (2)(2x + 5y)(3x?2y)。+7xy?3yx-=x2 +4xy-21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.注意:
1、必须做到不重复,不遗漏2、注意确定积中每一项的符号
3、结果应化为最简式
随堂练习(1) (m+2n)(m?2n);
(2) (2n +5)(n?3) ; ㈠计算: (3) (x+2y)2 ;
(4) (ax+b)(cx+d ) .本节课你的收获是什么?本节课你学到了什么?运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄ ̄合并同类项. 如何进行多项式与多项式乘法运算?
为a米的长方形林区增长了n米,加宽了b米,
请你表示这块林区现在的面积。ma你能用不同的形式表示所拼图的面积吗?manambnb这块林区现在长为(m+n)米,宽为(a+b)米。因而面积为(m+n)(a+b)米2
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb(a+b)X=(a+b)(m+n)=ma+ mb+ na+ nb根据以上问题,讨论得知:如何进行多项式与多项式相乘的 运算 ?实际上,把(m+n)看成一个整体,有:(m+n)(a+b)=(m+n)a+(m+n)b=ma+ mb+ na+ nb(m+n)(a+b)=ma+ mb+ na+ nb先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。例题解析 【例4】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。?3x+2x=x2 -x-6 -2×3(2) (3x -1)(2x+1)=3x?2x+3x? 1-1?2 x?1=6x2+3x-2 x?1=6x2 +x?1. 【例5】计算: (1)(x?3y)(x+7y), (2)(2x + 5y)(3x?2y)。+7xy?3yx-=x2 +4xy-21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.注意:
1、必须做到不重复,不遗漏2、注意确定积中每一项的符号
3、结果应化为最简式
随堂练习(1) (m+2n)(m?2n);
(2) (2n +5)(n?3) ; ㈠计算: (3) (x+2y)2 ;
(4) (ax+b)(cx+d ) .本节课你的收获是什么?本节课你学到了什么?运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄ ̄合并同类项. 如何进行多项式与多项式乘法运算?
