辽宁省沈阳市第120中学2022-2023学年高一下学期4月第一次质量检测数学试题(含答案)
文档属性
| 名称 | 辽宁省沈阳市第120中学2022-2023学年高一下学期4月第一次质量检测数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 861.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 13:50:32 | ||
图片预览




文档简介
沈阳市第120中学2022-2023学年度下学期
高一年级第一次质量检测
数学试卷
满分:150分 时间:120分钟
一、单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个符合题目要求
1.已知点O为坐标原点,点A是单位圆与x轴正半轴的交点,点B在第二象限.记且,
则( )
A. B. C. D.
2.已知向量,,向量在方向上的投影向量为( )
A. B. C. D.
3.已知函数.令,,,则( )
A. B. C. D.
4.已知单位向量,满足,若向量,则( )
A. B. C. D.
5.已知曲线,,则下面结论正确的是( )
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
6.已知函数(,)与直线交于A,B两点,且线段AB长度的最小值为,若将函数的图象向左平移个单位后恰好关于原点对称,则φ的最大值为( )
A. B. C. D.
7.若为第二象限角,且,则的值( )
A.4 B. C. D.
8.将函数和直线的所有交点从左到右依次记为,,,…,若P点坐标为,则( )
A.10 B.6 C.2 D.0
二、多项选择题:本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,至少有一个符合题目要求的,每道题全对得5分,部分选对得2分
9.设函数向左平移个单位长度得到函数,已知在上有且只有5个零点,则下列结论正确的是( )
A.的图象关于直线对称
B.在上有且只有3个最大值,在上有且只有2个最小值
C.在上单调递增
D.ω的取值范围是
10.对于函数,下列说法错误的是( )
A.函数的值域是
B.当且仅当时,
C.当且仅当时,函数取得最大值1
D.函数是以π为最小正周期的周期函数
11.高斯是德国著名数学家,近代数学奠基者之一,享有“数学王子”称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过x的最大整数,则称为高斯函数,例如,.已知函数,函数,则下列结论正确的是( )
A.函数的值域是 B.函数是周期函数
C.函数的图象关于对称 D.方程只有一个实数根.
12.奔驰定理:已知O是内的一点,,,的面积分别为,,,则.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz)的logo很相似,故形象地称其为“奔驰定理”.若O是锐角内的一点,A,B,C是的三个内角,且点O满足,则下列结论正确的是( )
参考公式:
A.O为的垂心 B.
C. D.
三、填空题:本大题共4小题,每小题5分,共20分
13.已知,则的值是______.
14.求函数的定义域为______.
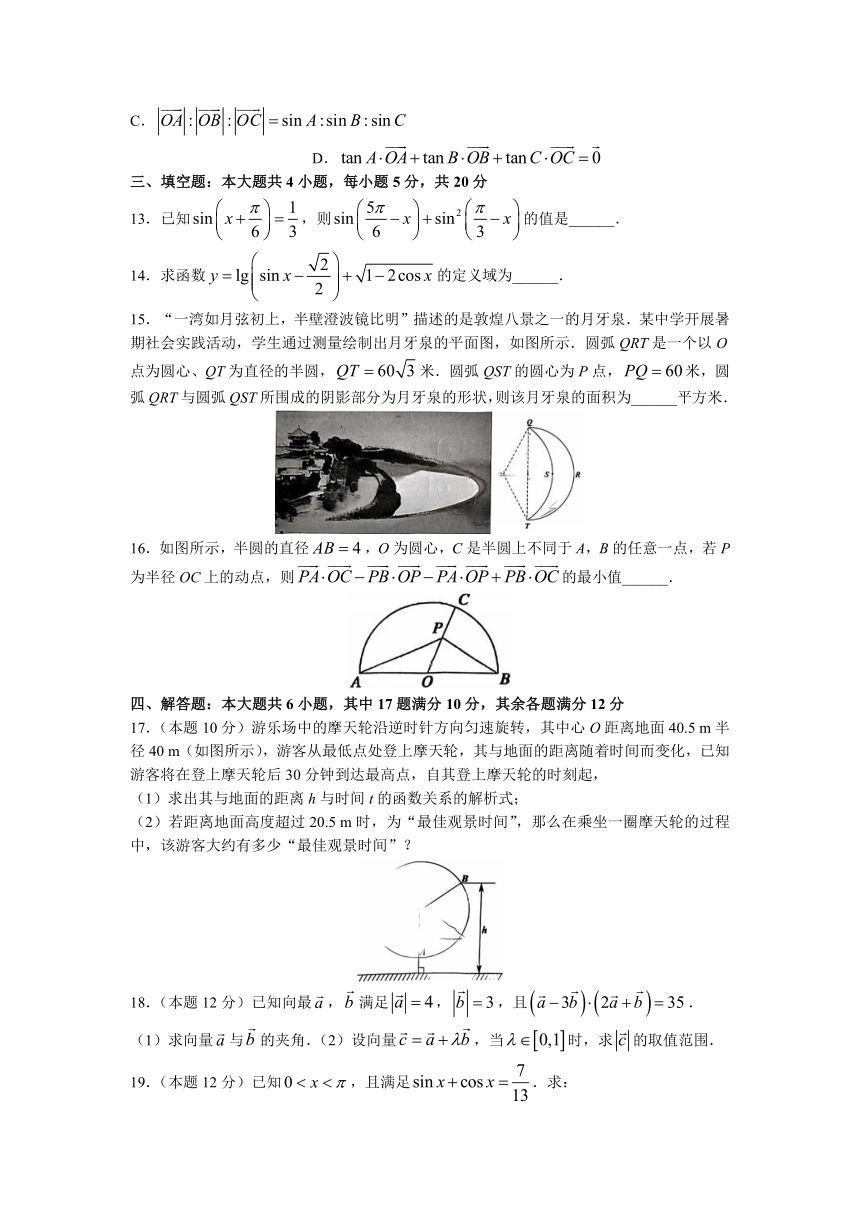
15.“一湾如月弦初上,半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.某中学开展暑期社会实践活动,学生通过测量绘制出月牙泉的平面图,如图所示.圆弧QRT是一个以O点为圆心、QT为直径的半圆,米.圆弧QST的圆心为P点,米,圆弧QRT与圆弧QST所围成的阴影部分为月牙泉的形状,则该月牙泉的面积为______平方米.
16.如图所示,半圆的直径,O为圆心,C是半圆上不同于A,B的任意一点,若P为半径OC上的动点,则的最小值______.
四、解答题:本大题共6小题,其中17题满分10分,其余各题满分12分
17.(本题10分)游乐场中的摩天轮沿逆时针方向匀速旋转,其中心O距离地面40.5 m半径40 m(如图所示),游客从最低点处登上摩天轮,其与地面的距离随着时间而变化,已知游客将在登上摩天轮后30分钟到达最高点,自其登上摩天轮的时刻起,
(1)求出其与地面的距离h与时间t的函数关系的解析式;
(2)若距离地面高度超过20.5 m时,为“最佳观景时间”,那么在乘坐一圈摩天轮的过程中,该游客大约有多少“最佳观景时间”?
18.(本题12分)已知向最,满足,,且.
(1)求向量与的夹角.(2)设向量,当时,求的取值范围.
19.(本题12分)已知,且满足.求:
(1)的值;(2);(3)
20.(本题12分)已知函数,.
(1)若的最小值为,求m的值;(2)当时,若对任意,都有恒成立,求实数a的取值范围.
21.(本题12分)函数(其中,,)的部分图象如图所示,把函数的图象向右平移个单位,得到函数的图象.
(1)当时,求函数的单调递减区间;
(2)对于,是否总存在唯一的实数,使得成立?若存在,求出实数m的值或取值范围;若不存在,说明理由.
22.(本题12分)如图,在中,,,,D为边BC的中点.
(1)求的值;
(2)若点P满足,求的最小值:
(3)若点P在∠BAC的角平分线上,且满足.若,求的取值范围.
沈阳市第120中学2022-2023学年度下学期
高一年级第一次数学质量检测
答案
一.单选题1.C 2.B 3.D 4.C 5.D 6.C 7.B 8.A
二.多选题9.CD 10.ACD 11.ABC 12.ABD
三.填空题:本大题共4小题,每小题5分,共20分
13. 14. 15. 16.
四.解答题:本大题共6小题,其中17题满分10分,其余各题满分12分
17.解:(1)设 (,),
则,,所以,
第一次到最高点旋转了半周期,所以,
游客从最低点登上,所以,故,(或)
(2)令,
则(或),
所以,
,,
所以,
因此,在乘坐一圈摩天轮的过程中,该游客大约有40 min最佳观景时间.
18.(本题12分)解:(1)因为.则.
因为,,则,解得.
设向量与的夹角为θ,则.又,则,所以向量与的夹角为.
(2)因为
,则.
因为,则当时,取最小值;
当时,取最大值4,所以的取值范围是.
19.(本题12分)解:(1)已知,且满足.
所以
∴,,
.
联立,解得,,.
(2)
(3)
.
20.(本题12分)
解:(1)函数.
当时,则,解得:,那么显然不成立
..令..
①当时,即,转化为
解得:,满足题意;
②当时,即,转化为
解得:,满足题意;
故得若的最小值为,m的值为4.5或;
(2)当时,,令.
∴转化为,其对称轴,∴上是递增函数.
.对任意.,都有恒成立,
,
可得:故得实数a的取值范围是.
21.(本题12分)
解:(1)由函数图象可知,,
,∴,,
∴,当时,,
∴,由得,∴,
由,得,
由,解得,.
∴函数的单调递减区间为.
(2)由,得,
由,可得,∴,
∴,
又,得,所以,
由的唯一性可得:即,
由,得,解得,
综上所述,当时,使成立.
22.(本题12分)解:(1)由勾股定理知,;
解法一(坐标法):建立平面直角坐标系,如图所示:
则,,,BC的中点,所以,,
所以;
解法二(基向量法):
;
解法三(定义法):
;
(2)由题意,点P在AC上,解法一(极化恒等式):
,
所以当PD⊥CA时,此时,
取到最小值,即;
解法二(坐标法):设,则,
所以的最小值是;
(3)解法一(坐标法):以AC,AB为x,y轴建立坐标系,
则∠BAC的角平分线方程为,可以设,
则可以表示为
,
所以,,
,
当时,的取值范围是.
解法二(几何法):由已知得,
则有,
即;
由①÷②得,所以,
所以,
所以.
高一年级第一次质量检测
数学试卷
满分:150分 时间:120分钟
一、单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个符合题目要求
1.已知点O为坐标原点,点A是单位圆与x轴正半轴的交点,点B在第二象限.记且,
则( )
A. B. C. D.
2.已知向量,,向量在方向上的投影向量为( )
A. B. C. D.
3.已知函数.令,,,则( )
A. B. C. D.
4.已知单位向量,满足,若向量,则( )
A. B. C. D.
5.已知曲线,,则下面结论正确的是( )
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
6.已知函数(,)与直线交于A,B两点,且线段AB长度的最小值为,若将函数的图象向左平移个单位后恰好关于原点对称,则φ的最大值为( )
A. B. C. D.
7.若为第二象限角,且,则的值( )
A.4 B. C. D.
8.将函数和直线的所有交点从左到右依次记为,,,…,若P点坐标为,则( )
A.10 B.6 C.2 D.0
二、多项选择题:本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,至少有一个符合题目要求的,每道题全对得5分,部分选对得2分
9.设函数向左平移个单位长度得到函数,已知在上有且只有5个零点,则下列结论正确的是( )
A.的图象关于直线对称
B.在上有且只有3个最大值,在上有且只有2个最小值
C.在上单调递增
D.ω的取值范围是
10.对于函数,下列说法错误的是( )
A.函数的值域是
B.当且仅当时,
C.当且仅当时,函数取得最大值1
D.函数是以π为最小正周期的周期函数
11.高斯是德国著名数学家,近代数学奠基者之一,享有“数学王子”称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过x的最大整数,则称为高斯函数,例如,.已知函数,函数,则下列结论正确的是( )
A.函数的值域是 B.函数是周期函数
C.函数的图象关于对称 D.方程只有一个实数根.
12.奔驰定理:已知O是内的一点,,,的面积分别为,,,则.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz)的logo很相似,故形象地称其为“奔驰定理”.若O是锐角内的一点,A,B,C是的三个内角,且点O满足,则下列结论正确的是( )
参考公式:
A.O为的垂心 B.
C. D.
三、填空题:本大题共4小题,每小题5分,共20分
13.已知,则的值是______.
14.求函数的定义域为______.
15.“一湾如月弦初上,半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.某中学开展暑期社会实践活动,学生通过测量绘制出月牙泉的平面图,如图所示.圆弧QRT是一个以O点为圆心、QT为直径的半圆,米.圆弧QST的圆心为P点,米,圆弧QRT与圆弧QST所围成的阴影部分为月牙泉的形状,则该月牙泉的面积为______平方米.
16.如图所示,半圆的直径,O为圆心,C是半圆上不同于A,B的任意一点,若P为半径OC上的动点,则的最小值______.
四、解答题:本大题共6小题,其中17题满分10分,其余各题满分12分
17.(本题10分)游乐场中的摩天轮沿逆时针方向匀速旋转,其中心O距离地面40.5 m半径40 m(如图所示),游客从最低点处登上摩天轮,其与地面的距离随着时间而变化,已知游客将在登上摩天轮后30分钟到达最高点,自其登上摩天轮的时刻起,
(1)求出其与地面的距离h与时间t的函数关系的解析式;
(2)若距离地面高度超过20.5 m时,为“最佳观景时间”,那么在乘坐一圈摩天轮的过程中,该游客大约有多少“最佳观景时间”?
18.(本题12分)已知向最,满足,,且.
(1)求向量与的夹角.(2)设向量,当时,求的取值范围.
19.(本题12分)已知,且满足.求:
(1)的值;(2);(3)
20.(本题12分)已知函数,.
(1)若的最小值为,求m的值;(2)当时,若对任意,都有恒成立,求实数a的取值范围.
21.(本题12分)函数(其中,,)的部分图象如图所示,把函数的图象向右平移个单位,得到函数的图象.
(1)当时,求函数的单调递减区间;
(2)对于,是否总存在唯一的实数,使得成立?若存在,求出实数m的值或取值范围;若不存在,说明理由.
22.(本题12分)如图,在中,,,,D为边BC的中点.
(1)求的值;
(2)若点P满足,求的最小值:
(3)若点P在∠BAC的角平分线上,且满足.若,求的取值范围.
沈阳市第120中学2022-2023学年度下学期
高一年级第一次数学质量检测
答案
一.单选题1.C 2.B 3.D 4.C 5.D 6.C 7.B 8.A
二.多选题9.CD 10.ACD 11.ABC 12.ABD
三.填空题:本大题共4小题,每小题5分,共20分
13. 14. 15. 16.
四.解答题:本大题共6小题,其中17题满分10分,其余各题满分12分
17.解:(1)设 (,),
则,,所以,
第一次到最高点旋转了半周期,所以,
游客从最低点登上,所以,故,(或)
(2)令,
则(或),
所以,
,,
所以,
因此,在乘坐一圈摩天轮的过程中,该游客大约有40 min最佳观景时间.
18.(本题12分)解:(1)因为.则.
因为,,则,解得.
设向量与的夹角为θ,则.又,则,所以向量与的夹角为.
(2)因为
,则.
因为,则当时,取最小值;
当时,取最大值4,所以的取值范围是.
19.(本题12分)解:(1)已知,且满足.
所以
∴,,
.
联立,解得,,.
(2)
(3)
.
20.(本题12分)
解:(1)函数.
当时,则,解得:,那么显然不成立
..令..
①当时,即,转化为
解得:,满足题意;
②当时,即,转化为
解得:,满足题意;
故得若的最小值为,m的值为4.5或;
(2)当时,,令.
∴转化为,其对称轴,∴上是递增函数.
.对任意.,都有恒成立,
,
可得:故得实数a的取值范围是.
21.(本题12分)
解:(1)由函数图象可知,,
,∴,,
∴,当时,,
∴,由得,∴,
由,得,
由,解得,.
∴函数的单调递减区间为.
(2)由,得,
由,可得,∴,
∴,
又,得,所以,
由的唯一性可得:即,
由,得,解得,
综上所述,当时,使成立.
22.(本题12分)解:(1)由勾股定理知,;
解法一(坐标法):建立平面直角坐标系,如图所示:
则,,,BC的中点,所以,,
所以;
解法二(基向量法):
;
解法三(定义法):
;
(2)由题意,点P在AC上,解法一(极化恒等式):
,
所以当PD⊥CA时,此时,
取到最小值,即;
解法二(坐标法):设,则,
所以的最小值是;
(3)解法一(坐标法):以AC,AB为x,y轴建立坐标系,
则∠BAC的角平分线方程为,可以设,
则可以表示为
,
所以,,
,
当时,的取值范围是.
解法二(几何法):由已知得,
则有,
即;
由①÷②得,所以,
所以,
所以.
同课章节目录
