因式分解(提公因式)[上学期]
图片预览




文档简介
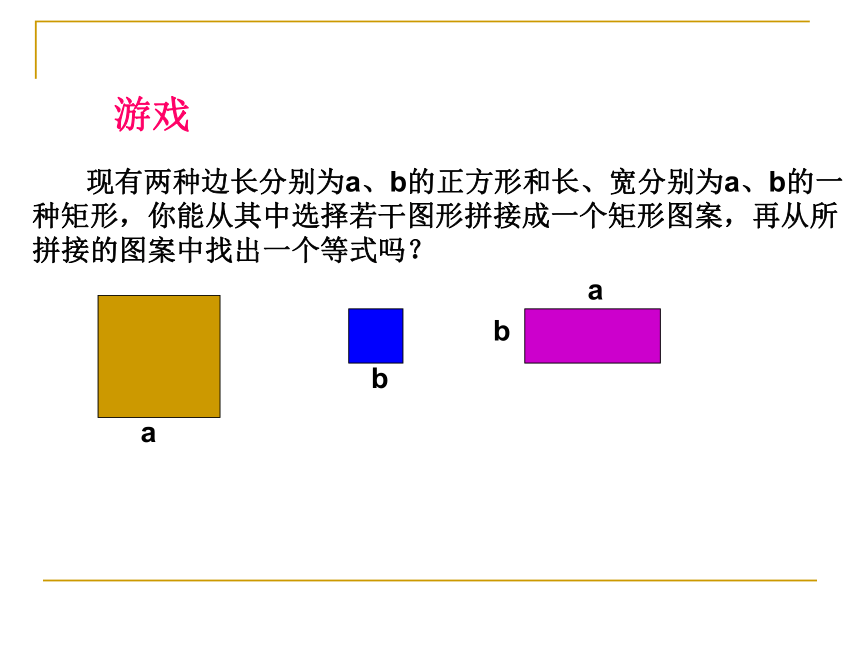
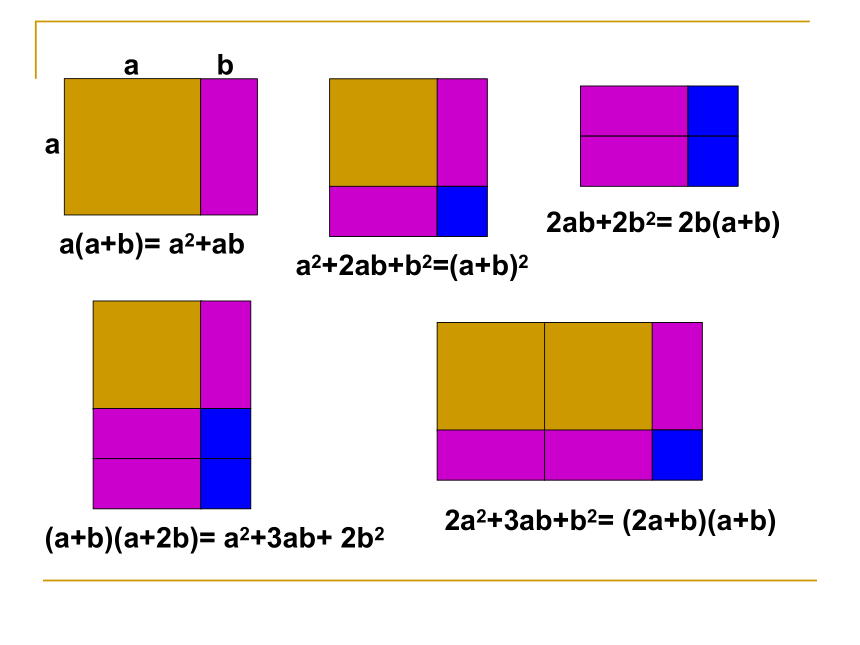
课件19张PPT。游戏 现有两种边长分别为a、b的正方形和长、宽分别为a、b的一种矩形,你能从其中选择若干图形拼接成一个矩形图案,再从所拼接的图案中找出一个等式吗?a(a+b)= a2+aba2+2ab+b2=(a+b)22ab+2b2= 2b(a+b)(a+b)(a+2b)= a2+3ab+ 2b22a2+3ab+b2= (2a+b)(a+b)1、因式分解的概念
把一个多项式化为几个整式的乘积形式,这就是因式分解。2、因式分解与整式乘法的关系 ◆ 因式分解的特点:由和差形式(多项式)转化成整式的积的形式;
◆ 整式乘法的特点:由整式积的形式转化成和差形式(多项式)。 判断是否是因式分解
要看等式的左边是否是一
个多项式,右边是否是几
个整式的积的形式。试一试:
下列由左边到右边的变形中,哪些是因式分解,哪些不是?
(1) ( )
(2)(x+2)(x-2)= x2-4( )
(3)a2-b2+1=(a+b)(a-b)+1( )
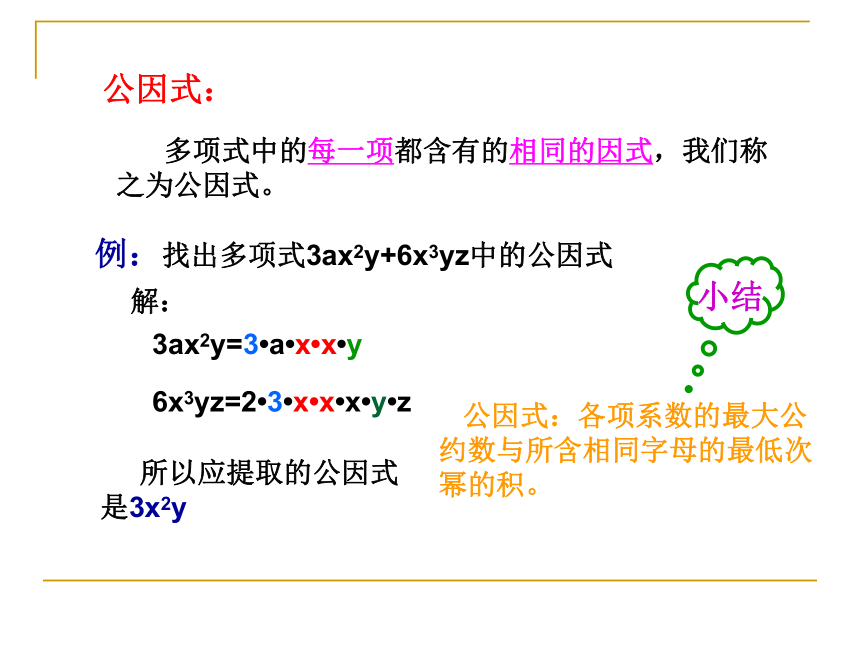
(4)ax2+ay2=a(x2+y2) ( )例:找出多项式3ax2y+6x3yz中的公因式公因式: 多项式中的每一项都含有的相同的因式,我们称之为公因式。解:3ax2y=3?a?x?x?y
6x3yz=2?3?x?x?x?y?z 公因式:各项系数的最大公约数与所含相同字母的最低次幂的积。 所以应提取的公因式
是3x2y找出下列式子中的公因式:
4a3,8a2b2,-30a2bc (2) 2x3y4, -10x2y3,2x2y2
(3) 4x (y-x)2,6x (x-y)2 (4) 3a(x-y), 9b(y-x)
(5) a2bn, 2abn+2试一试( 2a2b )( 2x2y2 )( 2x (x-y)2 )( 3 (x-y) )( abn )因为 多项式3ax2y+6x3yz的公因式是3x2y所以 3ax2y+6x3yz= 3x2y(a+2xz) 另一个因式a+2xz是如何得到的?提公因式法引例:提公因式法的一般步骤:1、确定应提取的公因式;2、用公因式去除这个多项式,所得的商作为另一个因式;3、把多项式写成两个因式的积的形式。例题解析 例1、用提公因式法分解因式:
(1)2x3+6x2+2x
(2) a3bc3+2a2b2c2-3a2b3c
(3) -3an+2+2an+1-7an友情提示: (1)如果多项式的某一项正好是公因式,要注意该项在提取了公因式后,应该用“1”顶替它原来的位置,切不可把“1”漏掉。(2)如果多项式的第一项有“—”号,一般都将“—”号随公因式一起提出。 随堂热身1、下列各式的因式分解中正确的是( )
(A)12xyz-9x2y2=3xyz(4-3xy)
(B)3a2y-3ay+6y=3y(a2-a+2)
(C) –8a3b2c+6a2b2c2-12a3bc2= -2a2bc(4ab+3bc-6ac)
(D)a2b+5ab-b=b(a2+5a)B 2、把下列多项式分解因式:
(1)12x2y+18xy2; (2)-x2+xy-xz; (3)2x3+6x2+2x
现有甲、乙、丙三位同学各做一题,他们的解法如下:
聪明的同学你认为他们的解法正确吗?试说明理由。
甲同学:
解:12x2y+18xy2
=3xy(4x+6y)
乙同学:
解:-x2+xy-xz
=-x(x+y-z)丙同学:
解:2x3+6x2+2x
=2x(x2+3x)
3、把下列多项式因式分解:
(1) 4ab-2a2b; (2)-3ab+6abx-9aby
(3) -24m2x+16n2x; (4)anb2-2anb.3、用简便方法计算: 想一想 (1)已知x+y=2,xy=-3,则x2y+xy2=_____.
(2)(-2)2005+(-2)2006=______.
(3)你知道523-521能被120整除吗?试说明你的理由。
-622005 隧道的横截面如图,用关于h、r的多项式表示隧道横截面的面积。这个多项式能分解因式吗?若r=7米,h=2∏米,计算这个隧道的横截面面积。应用于生活拓展一 1、把下列各式分解因式: (1)2m(x+y)+n(x+y);
(2)a(p-q)-4b(q-p);
(3)4a(x-y)2-2b(y-x)2;
(4)2(a-3)2-a+3.
整体思想是数学中一种重要而且常用的思想方法 公因式既可以是一个单项式的形式,也可以是一个多项式的形式让我们一起总结一下
用提公因式法分解因式应注意的问题:小小数学家 今年是2005年,这儿有一道与2005有关的计算
题。已知x3+x2+x+1=0,求1+x+x2+x3+…+x2005的
值。聪明的同学,你能得到这个计算结果吗? 在学习本节课的过程中,你的脑海里曾经闪过一些奇思妙想或着遇到过一些困难吗?让我们一起交流一下吧!
说说心里话谢 谢 !祝同学们:
学业有成,心想事成!
把一个多项式化为几个整式的乘积形式,这就是因式分解。2、因式分解与整式乘法的关系 ◆ 因式分解的特点:由和差形式(多项式)转化成整式的积的形式;
◆ 整式乘法的特点:由整式积的形式转化成和差形式(多项式)。 判断是否是因式分解
要看等式的左边是否是一
个多项式,右边是否是几
个整式的积的形式。试一试:
下列由左边到右边的变形中,哪些是因式分解,哪些不是?
(1) ( )
(2)(x+2)(x-2)= x2-4( )
(3)a2-b2+1=(a+b)(a-b)+1( )
(4)ax2+ay2=a(x2+y2) ( )例:找出多项式3ax2y+6x3yz中的公因式公因式: 多项式中的每一项都含有的相同的因式,我们称之为公因式。解:3ax2y=3?a?x?x?y
6x3yz=2?3?x?x?x?y?z 公因式:各项系数的最大公约数与所含相同字母的最低次幂的积。 所以应提取的公因式
是3x2y找出下列式子中的公因式:
4a3,8a2b2,-30a2bc (2) 2x3y4, -10x2y3,2x2y2
(3) 4x (y-x)2,6x (x-y)2 (4) 3a(x-y), 9b(y-x)
(5) a2bn, 2abn+2试一试( 2a2b )( 2x2y2 )( 2x (x-y)2 )( 3 (x-y) )( abn )因为 多项式3ax2y+6x3yz的公因式是3x2y所以 3ax2y+6x3yz= 3x2y(a+2xz) 另一个因式a+2xz是如何得到的?提公因式法引例:提公因式法的一般步骤:1、确定应提取的公因式;2、用公因式去除这个多项式,所得的商作为另一个因式;3、把多项式写成两个因式的积的形式。例题解析 例1、用提公因式法分解因式:
(1)2x3+6x2+2x
(2) a3bc3+2a2b2c2-3a2b3c
(3) -3an+2+2an+1-7an友情提示: (1)如果多项式的某一项正好是公因式,要注意该项在提取了公因式后,应该用“1”顶替它原来的位置,切不可把“1”漏掉。(2)如果多项式的第一项有“—”号,一般都将“—”号随公因式一起提出。 随堂热身1、下列各式的因式分解中正确的是( )
(A)12xyz-9x2y2=3xyz(4-3xy)
(B)3a2y-3ay+6y=3y(a2-a+2)
(C) –8a3b2c+6a2b2c2-12a3bc2= -2a2bc(4ab+3bc-6ac)
(D)a2b+5ab-b=b(a2+5a)B 2、把下列多项式分解因式:
(1)12x2y+18xy2; (2)-x2+xy-xz; (3)2x3+6x2+2x
现有甲、乙、丙三位同学各做一题,他们的解法如下:
聪明的同学你认为他们的解法正确吗?试说明理由。
甲同学:
解:12x2y+18xy2
=3xy(4x+6y)
乙同学:
解:-x2+xy-xz
=-x(x+y-z)丙同学:
解:2x3+6x2+2x
=2x(x2+3x)
3、把下列多项式因式分解:
(1) 4ab-2a2b; (2)-3ab+6abx-9aby
(3) -24m2x+16n2x; (4)anb2-2anb.3、用简便方法计算: 想一想 (1)已知x+y=2,xy=-3,则x2y+xy2=_____.
(2)(-2)2005+(-2)2006=______.
(3)你知道523-521能被120整除吗?试说明你的理由。
-622005 隧道的横截面如图,用关于h、r的多项式表示隧道横截面的面积。这个多项式能分解因式吗?若r=7米,h=2∏米,计算这个隧道的横截面面积。应用于生活拓展一 1、把下列各式分解因式: (1)2m(x+y)+n(x+y);
(2)a(p-q)-4b(q-p);
(3)4a(x-y)2-2b(y-x)2;
(4)2(a-3)2-a+3.
整体思想是数学中一种重要而且常用的思想方法 公因式既可以是一个单项式的形式,也可以是一个多项式的形式让我们一起总结一下
用提公因式法分解因式应注意的问题:小小数学家 今年是2005年,这儿有一道与2005有关的计算
题。已知x3+x2+x+1=0,求1+x+x2+x3+…+x2005的
值。聪明的同学,你能得到这个计算结果吗? 在学习本节课的过程中,你的脑海里曾经闪过一些奇思妙想或着遇到过一些困难吗?让我们一起交流一下吧!
说说心里话谢 谢 !祝同学们:
学业有成,心想事成!
