第6单元圆能力提升检测卷(单元测试)小学数学五年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元圆能力提升检测卷(单元测试)小学数学五年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 22:06:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第6单元圆能力提升检测卷(单元测试)-小学数学五年级下册苏教版
一、选择题
1.下列各图中的正方形面积相等,图( )的阴影面积与另外两图不同。
A. B. C.
2.一个圆,半径扩大到原来的2倍,那么周长( )。
A.不变 B.也扩大到原来的2倍 C.扩大到原来的4倍
3.如下图,小圆的直径和大圆的半径相等,大圆的面积是小圆的( )倍。
A.2 B.3.14 C.4
4.在一张长8分米、宽6分米的长方形彩纸上画一个尽可能大的圆.这个圆的面积是( ).
A.50.24平方分米 B.28.26平方分米 C.113.04平方分米
5.把一个半径是1厘米的圆平均分成若干份,剪开拼成一个近似的长方形。这个长方形的周长是( )厘米。
A.14.56 B.10.28 C.8.28
6.一个圆的半径5厘米,对折后剪成两个同样大的半圆,每个半圆的周长是( )。
A.15.7厘米 B.31.4厘米 C.25.7厘米
二、填空题
7.在推导圆的面积公式时,把圆分成若干等份,拼成一个近似的长方形。如果拼成的近似长方形的长是9.42厘米,那么圆的周长是( )厘米,圆的面积是( )平方厘米。
8.周长是18.84厘米的圆,它的直径是( )厘米,面积是( )平方厘米。
9.一个圆环,内圆的半径2厘米,外圆直径6厘米,圆环的面积是( )平方厘米。
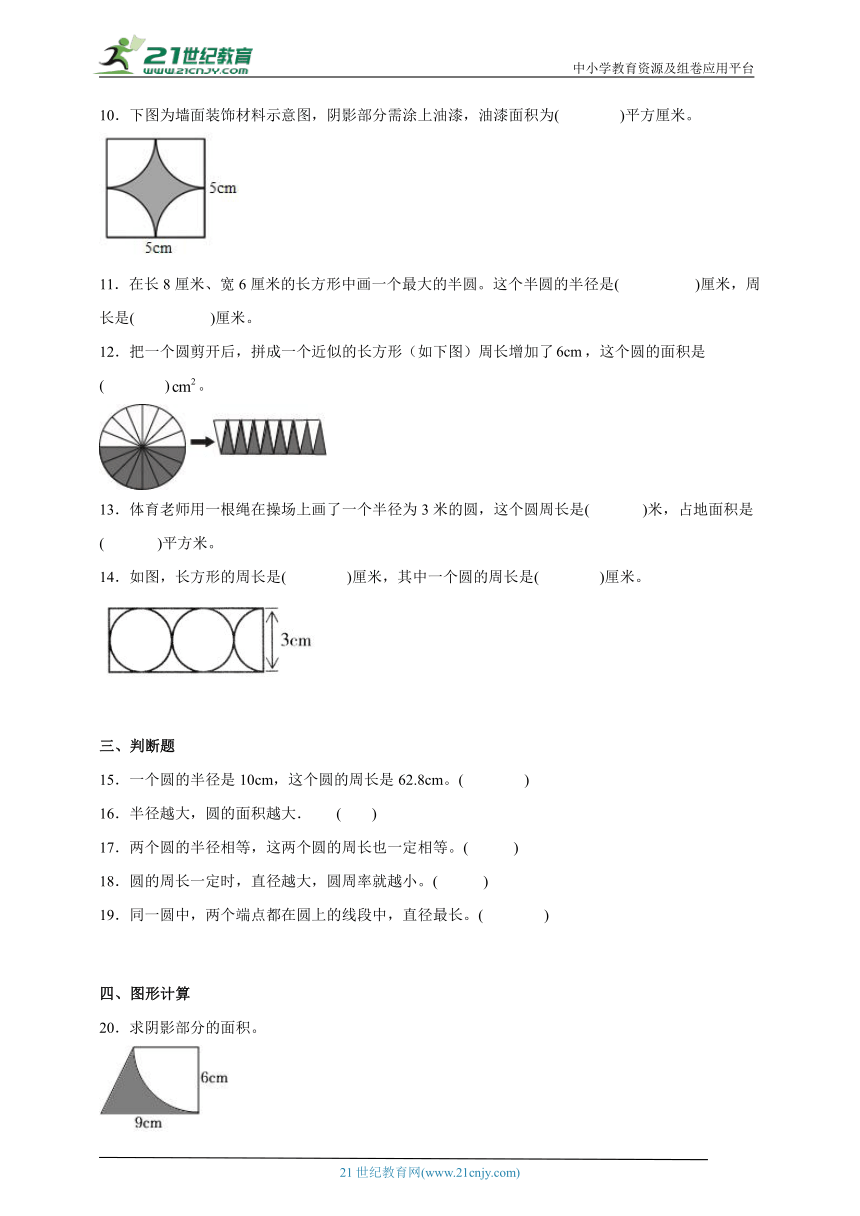
10.下图为墙面装饰材料示意图,阴影部分需涂上油漆,油漆面积为( )平方厘米。
11.在长8厘米、宽6厘米的长方形中画一个最大的半圆。这个半圆的半径是( )厘米,周长是( )厘米。
12.把一个圆剪开后,拼成一个近似的长方形(如下图)周长增加了,这个圆的面积是( )。
13.体育老师用一根绳在操场上画了一个半径为3米的圆,这个圆周长是( )米,占地面积是( )平方米。
14.如图,长方形的周长是( )厘米,其中一个圆的周长是( )厘米。
三、判断题
15.一个圆的半径是10cm,这个圆的周长是62.8cm。( )
16.半径越大,圆的面积越大. ( )
17.两个圆的半径相等,这两个圆的周长也一定相等。( )
18.圆的周长一定时,直径越大,圆周率就越小。( )
19.同一圆中,两个端点都在圆上的线段中,直径最长。( )
四、图形计算
20.求阴影部分的面积。
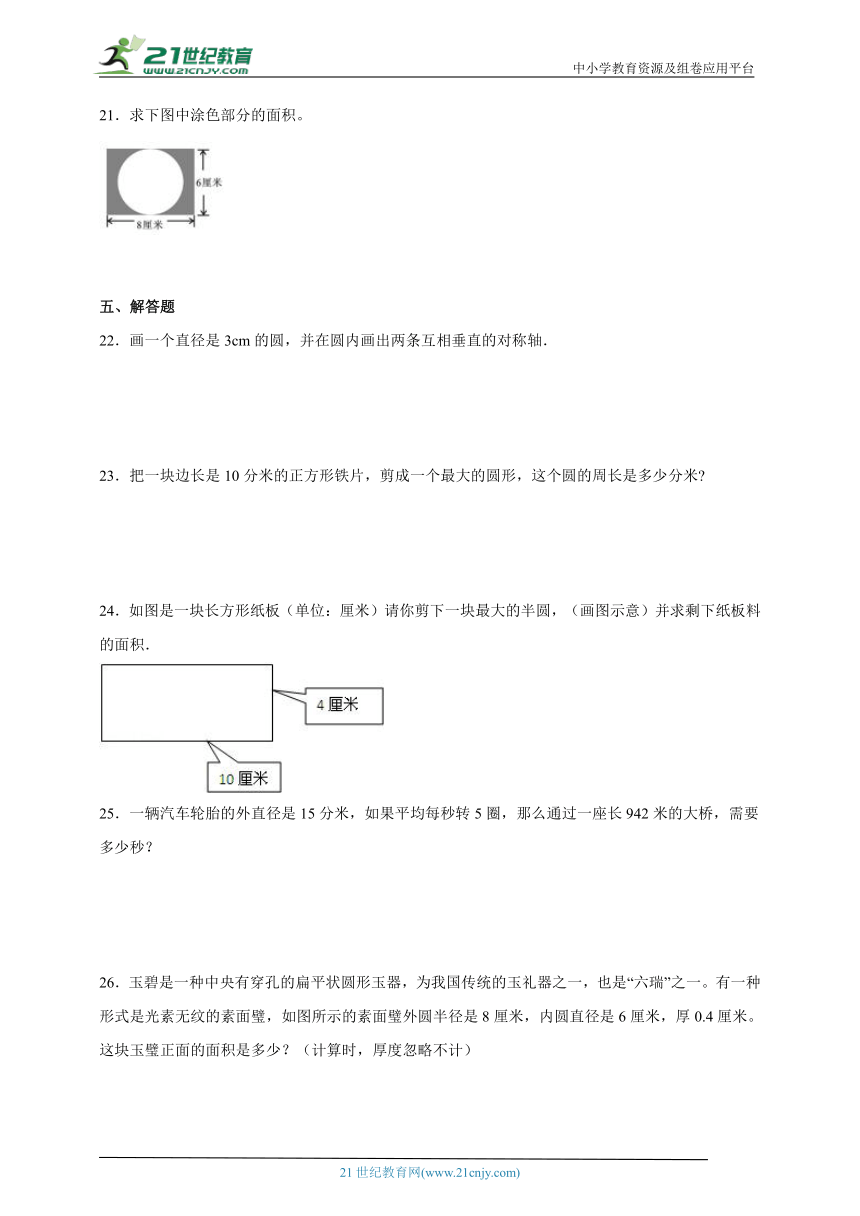
21.求下图中涂色部分的面积。
五、解答题
22.画一个直径是3cm的圆,并在圆内画出两条互相垂直的对称轴.
23.把一块边长是10分米的正方形铁片,剪成一个最大的圆形,这个圆的周长是多少分米
24.如图是一块长方形纸板(单位:厘米)请你剪下一块最大的半圆,(画图示意)并求剩下纸板料的面积.
25.一辆汽车轮胎的外直径是15分米,如果平均每秒转5圈,那么通过一座长942米的大桥,需要多少秒?
26.玉碧是一种中央有穿孔的扁平状圆形玉器,为我国传统的玉礼器之一,也是“六瑞”之一。有一种形式是光素无纹的素面璧,如图所示的素面璧外圆半径是8厘米,内圆直径是6厘米,厚0.4厘米。这块玉璧正面的面积是多少?(计算时,厚度忽略不计)
27.如图,王叔叔用9.42米长的篱笆靠墙围了一个最大的养鸡场,这个养鸡场的面积是多少平方米?如果每只鸡占地0.2平方米,这个养鸡场最多可以养多少只鸡?(根据实际情况,结果保留整数)
参考答案:
1.B
【分析】根据题意,阴影部分的面积=正方形的面积-空白部分的面积,据此逐项分析即可作出选择。
【详解】由分析得:
A.阴影部分的面积=正方形的面积-以正方形边长为直径的圆的面积;
B.阴影部分的面积=正方形的面积-正方形面积的一半;
C.阴影部分的面积等于正方形的面积-以正方形边长为直径的圆的面积。
所以下列各图中的正方形面积相等,图B的阴影面积与另外两图不同。
故答案为:B
【点睛】此题考查了阴影部分的面积的求法,将阴影面积转化为规则的图形的面积的差或和是解题的常用方法。
2.B
【分析】根据圆的周长与半径成正比例,可知圆周长扩大的倍数与圆的半径扩大的倍数相同。
【详解】略
3.C
【分析】小圆的直径和大圆的半径相等,说明大圆的半径是小圆半径的2倍,利用圆的面积公式和积的变化规律得出正确答案进行选择。
【详解】小圆的直径和大圆的半径相等,说明大圆的半径是小圆半径的2倍,圆的面积S=πr2,根据积的变化规律可得:r扩大2倍,r2就扩大2×2=4倍,所以大圆的面积是小圆面积的4倍;
故答案为:C
【点睛】此题考查的是积的变化规律在圆的面积公式中的灵活运用;这里可以得出结论:圆的半径扩大几倍,圆的面积就扩大倍数的平方。
4.B
【详解】思路分析:本题主要考查圆的面积的计算.首先确定在长方形纸上画一个最大的圆的直径是多少,然后根据圆的面积公式进行计算.
名师详解:先弄清在这个长方形彩纸上画一个尽可能大的圆的直径应该等于长方形的宽,然后根据圆的面积S=πr ,得出3.14×=28.26(平方分米).
易错提示:确定圆的直径是解题关键,圆的直径应与长方形的宽相等.
5.C
【分析】长方形的周长=圆的周长+半径×2,圆的周长=πd,据此解答。
【详解】3.14×1×2+1×2
=6.28+2
=8.28(厘米)
故选择:C
【点睛】明确长方形比圆的周长多两个半径的长度,掌握圆的周长计算公式是解题关键。
6.C
【分析】根据圆的周长公式:周长=π×2×半径,代入数据,求出这个圆的周长,再除以2,求出圆周长的一半,再加上这个半圆的直径,就是这个半圆的周长,据此解答。
【详解】3.14×2×5÷2+5×2
=6.28×5÷2+10
=31.4÷2+10
=15.7+10
=25.7(厘米)
故答案为:C
【点睛】解答本题的关键是熟记圆柱的周长公式,关键明确半圆的周长需要加上半圆的直径。
7. 18.84 28.26
【分析】根据题意可知,剪拼成的长方形的长就是圆周长的一半,据此求出圆的周长;再根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,求出半径;再根据圆的面积公式:π×半径2;代入数据,即可解答。
【详解】9.42×2=18.18(厘米)
18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
【点睛】熟练掌握圆的面积公式推导过程是解答本题的关键。
8. 6 28.26
【详解】略
9.15.7
【解析】略
10.5.375
【分析】根据图形可知,阴影部分面积=边长是5厘米的正方形面积-半径是(5÷2)的圆的面积,根据正方形面积公式:边长×边长;圆的面积公式:π×半径2,代入数据,即可解答。
【详解】5×5-3.14×(5÷2)2
=25-3.14×2.52
=25-3.14×6.25
=25-19.625
=5.375(平方厘米)
【点睛】利用长方形面积公式和圆的面积公式进行解答。
11. 4 20.56
【分析】在长8厘米、宽6厘米的长方形中画一个最大的半圆,半圆直径是这个长方形的长,则半圆的半径=直径÷2;根据半圆周长=圆周长的一半+直径。
【详解】8÷2=4(厘米)
周长:3.14×8÷2+8
=12.56+8
=20.56(厘米)
【点睛】关键是确定圆的直径是解题的关键,同时要注意半圆的周长是圆的周长一半加上直径的长度。
12.28.26
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,面积不变,拼成的长方形的长等于圆周长的一半,宽等于圆的半径,已知拼成的长方形的周长比圆的周长增加6厘米,也就是增加了2个半径,据此可以求出圆的半径,再根据圆的面积公式:S=πr2,求出圆的面积。
【详解】3.14×(6÷2)2
=3.14×9
=28.26()
【点睛】本题主要考查圆的面积公式的灵活运用,关键是熟记公式。
13. 18.84 28.26
【分析】根据圆形的周长公式:C=2πr,面积公式:S=πr2,将数据代入计算即可。
【详解】周长:
2×3×3.14
=6×3.14
=18.84(米)
面积:
3.14×32
=3.14×9
=28.26(平方米)
体育老师用一根绳在操场上画了一个半径为3米的圆,这个圆周长是18.84米,占地面积是28.26平方米。
【点睛】此题考查了圆的周长与面积计算,关键能够熟记公式。
14. 21 9.42
【分析】通过观察图形可知,长方形的长等于圆直径的2.5倍,宽等于圆的直径,根据长方形的周长=(长+宽)×2,圆的周长公式:C=πd,把数据代入公式解答。
【详解】(3×2.5+3)×2
=(7.5+3)×2
=10.5×2
=21(厘米)
3.14×3=9.42(厘米)
长方形的周长是21厘米,一个圆的周长是9.42厘米。
【点睛】此题主要考查长方形的周长公式、圆的周长公式的灵活运用,关键是熟记公式。
15.√
【分析】根据圆的周长公式C=2πr代入数据,即可判断。
【详解】2×3.14×10
=3.14×20
=62.8(cm)
一个圆的半径是10cm,这个圆的周长是62.8cm,此说法正确。
故答案为:√
【点睛】此题主要考查了圆的周长计算公式。
16.√
【解析】略
17.√
【分析】根据公式圆的周长C=2πr,半径相等,2和π为定值,所以半径相等周长一定相等,据此解答。
【详解】根据分析可得,两个圆的半径相等,这两个圆的周长也一定相等。原题说法正确;
故答案为:√。
【点睛】本题考查了圆的周长定义,圆的周长与半径和直径有关,半径或直径相等的圆周长一定相等。
18.×
【分析】圆周率是圆的周长与直径的比值,是一个固定不变的数,不随直径的变化而变化,据此判断即可。
【详解】圆周率=圆的周长÷直径,因为圆周率是一个定值,所以周长一定时,直径也一定,故原题说法错误。
故答案为:×
【点睛】本题考查对圆周率的认识,需掌握圆周率的定义。
19.√
【分析】两个端点都在圆上的线段中,经过圆心的线段最长,也就是圆的直径。
【详解】在同一个圆中,两个端点都在圆上的线段中,直径最长。原题说法正确。
故答案为:√
【点睛】此题考查的是圆的有关知识的理解,圆内所有的线段中,直径最长。
20.
【分析】从图上可得:用梯形的面积减去半圆的面积,即可得出答案。半圆的半径是,所以梯形的上底是,又因为这是一个直角梯形,所以梯形的高等于半圆的半径。将数据代入梯形面积公式(上底下底)高和半圆的面积公式,即可得出答案。
【详解】(6+9)×6÷2-×3.14×62
=15×6÷2-0.785×36
=90÷2-28.26
=45-28.26
=16.74(cm2)
阴影部分的面积是16.74 cm2。
21.19.74平方厘米
【分析】通过观察图形可知,涂色部分的面积等于长方形的面积减去圆的面积,根据长方形的面积公式:S=ab,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】8×6-3.14×(6÷2)2
=48-3.14×9
=48-28.26
=19.74(平方厘米)
涂色部分的面积是19.74平方厘米。
22.如图
【详解】试题分析:(1)圆心确定圆的位置,半径确定圆的大小,由此以点O为圆心,以3÷2=1.5厘米为半径画圆;
(2)圆的对称轴有无数条,分别是经过圆心的直线,由此经过圆心画出两条互相垂直的直线即可.
解:以点O为圆心,以3÷2=1.5厘米为半径画圆,并画出它的互相垂直的两条对称轴如图所示:
点评:此题考查了利用圆的两大要素:圆心与半径画圆的方法,以及利用轴对称图形的定义确定圆的对称轴位置的方法的灵活应用.
23.31.4分米
【详解】3.14×10=31.4(分米)
24.如图,剩下的纸板的面积是14.88平方厘米
【详解】试题分析:(1)根据长方形内最大的半圆的半径特点可知:这个半圆的半径是4厘米,由此即可在图中画出这个半圆,
(2)剩下的纸板料的面积就等于长方形的面积减去半圆的面积,由此利用长方形和圆的面积公式即可解答.
解:(1)观察图形可知,半圆的半径是4厘米,由此以长方形的一条长的中点为圆心,以4厘米为半径,在这个长方形纸板上画出这个半圆如图所示:
;
(2)10×4﹣3.14×42÷2,
=40﹣25.12,
=14.88(平方厘米),
答:剩下的纸板的面积是14.88平方厘米.
点评:此题考查了长方形内最大的半圆的画法以及长方形与圆的面积公式的灵活应用.
25.40秒
【分析】先求出轮胎的周长,根据圆的周长公式:,再用轮胎的周长×5圈,求出1秒钟轮胎转多少米,再用大桥的长度除以轮胎一秒钟转的米数,即可解答。
【详解】15分米=1.5米
942÷(3.14×1.5×5)
=942÷(4.71×5)
=942÷23.55
=40(秒)
答:需要40秒。
【点睛】本题考查圆的周长公式的应用,关键是熟记公式,注意单位名数的统一。
26.172.7平方厘米
【分析】根据题意,求这块玉璧的正面的面积,就是求圆环的面积,根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,即可解答。
【详解】内圆的半径:6÷2=3(厘米)
3.14×(82-32)
=3.14×(64-9)
=3.14×55
=172.7(平方厘米)
答:这块玉璧正面的面积是172.7平方厘米。
【点睛】熟练掌握圆环的面积公式是解答本题的关键。
27.28.26平方米;141只
【分析】观察图形可知,养鸡场的面积是圆的面积的;已知圆周长的的长度,根据圆的周长公式:周长=π×2×半径;半径=周长÷2÷π;代入数据,求出这个圆的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出这个圆的面积,再除以4,即可求出这个养鸡场的面积;再用养鸡场的面积÷每只鸡占地面积,即可解答。
【详解】9.42×4÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
3.14×62÷4
=3.14×36÷4
=113.04÷4
=28.26(平方米)
28.26÷0.2≈141(只)
答:这个养鸡场的面积是28.26平方米;这个养鸡场最多可以养141只鸡。
【点睛】利用圆的周长公式、面积公式进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元圆能力提升检测卷(单元测试)-小学数学五年级下册苏教版
一、选择题
1.下列各图中的正方形面积相等,图( )的阴影面积与另外两图不同。
A. B. C.
2.一个圆,半径扩大到原来的2倍,那么周长( )。
A.不变 B.也扩大到原来的2倍 C.扩大到原来的4倍
3.如下图,小圆的直径和大圆的半径相等,大圆的面积是小圆的( )倍。
A.2 B.3.14 C.4
4.在一张长8分米、宽6分米的长方形彩纸上画一个尽可能大的圆.这个圆的面积是( ).
A.50.24平方分米 B.28.26平方分米 C.113.04平方分米
5.把一个半径是1厘米的圆平均分成若干份,剪开拼成一个近似的长方形。这个长方形的周长是( )厘米。
A.14.56 B.10.28 C.8.28
6.一个圆的半径5厘米,对折后剪成两个同样大的半圆,每个半圆的周长是( )。
A.15.7厘米 B.31.4厘米 C.25.7厘米
二、填空题
7.在推导圆的面积公式时,把圆分成若干等份,拼成一个近似的长方形。如果拼成的近似长方形的长是9.42厘米,那么圆的周长是( )厘米,圆的面积是( )平方厘米。
8.周长是18.84厘米的圆,它的直径是( )厘米,面积是( )平方厘米。
9.一个圆环,内圆的半径2厘米,外圆直径6厘米,圆环的面积是( )平方厘米。
10.下图为墙面装饰材料示意图,阴影部分需涂上油漆,油漆面积为( )平方厘米。
11.在长8厘米、宽6厘米的长方形中画一个最大的半圆。这个半圆的半径是( )厘米,周长是( )厘米。
12.把一个圆剪开后,拼成一个近似的长方形(如下图)周长增加了,这个圆的面积是( )。
13.体育老师用一根绳在操场上画了一个半径为3米的圆,这个圆周长是( )米,占地面积是( )平方米。
14.如图,长方形的周长是( )厘米,其中一个圆的周长是( )厘米。
三、判断题
15.一个圆的半径是10cm,这个圆的周长是62.8cm。( )
16.半径越大,圆的面积越大. ( )
17.两个圆的半径相等,这两个圆的周长也一定相等。( )
18.圆的周长一定时,直径越大,圆周率就越小。( )
19.同一圆中,两个端点都在圆上的线段中,直径最长。( )
四、图形计算
20.求阴影部分的面积。
21.求下图中涂色部分的面积。
五、解答题
22.画一个直径是3cm的圆,并在圆内画出两条互相垂直的对称轴.
23.把一块边长是10分米的正方形铁片,剪成一个最大的圆形,这个圆的周长是多少分米
24.如图是一块长方形纸板(单位:厘米)请你剪下一块最大的半圆,(画图示意)并求剩下纸板料的面积.
25.一辆汽车轮胎的外直径是15分米,如果平均每秒转5圈,那么通过一座长942米的大桥,需要多少秒?
26.玉碧是一种中央有穿孔的扁平状圆形玉器,为我国传统的玉礼器之一,也是“六瑞”之一。有一种形式是光素无纹的素面璧,如图所示的素面璧外圆半径是8厘米,内圆直径是6厘米,厚0.4厘米。这块玉璧正面的面积是多少?(计算时,厚度忽略不计)
27.如图,王叔叔用9.42米长的篱笆靠墙围了一个最大的养鸡场,这个养鸡场的面积是多少平方米?如果每只鸡占地0.2平方米,这个养鸡场最多可以养多少只鸡?(根据实际情况,结果保留整数)
参考答案:
1.B
【分析】根据题意,阴影部分的面积=正方形的面积-空白部分的面积,据此逐项分析即可作出选择。
【详解】由分析得:
A.阴影部分的面积=正方形的面积-以正方形边长为直径的圆的面积;
B.阴影部分的面积=正方形的面积-正方形面积的一半;
C.阴影部分的面积等于正方形的面积-以正方形边长为直径的圆的面积。
所以下列各图中的正方形面积相等,图B的阴影面积与另外两图不同。
故答案为:B
【点睛】此题考查了阴影部分的面积的求法,将阴影面积转化为规则的图形的面积的差或和是解题的常用方法。
2.B
【分析】根据圆的周长与半径成正比例,可知圆周长扩大的倍数与圆的半径扩大的倍数相同。
【详解】略
3.C
【分析】小圆的直径和大圆的半径相等,说明大圆的半径是小圆半径的2倍,利用圆的面积公式和积的变化规律得出正确答案进行选择。
【详解】小圆的直径和大圆的半径相等,说明大圆的半径是小圆半径的2倍,圆的面积S=πr2,根据积的变化规律可得:r扩大2倍,r2就扩大2×2=4倍,所以大圆的面积是小圆面积的4倍;
故答案为:C
【点睛】此题考查的是积的变化规律在圆的面积公式中的灵活运用;这里可以得出结论:圆的半径扩大几倍,圆的面积就扩大倍数的平方。
4.B
【详解】思路分析:本题主要考查圆的面积的计算.首先确定在长方形纸上画一个最大的圆的直径是多少,然后根据圆的面积公式进行计算.
名师详解:先弄清在这个长方形彩纸上画一个尽可能大的圆的直径应该等于长方形的宽,然后根据圆的面积S=πr ,得出3.14×=28.26(平方分米).
易错提示:确定圆的直径是解题关键,圆的直径应与长方形的宽相等.
5.C
【分析】长方形的周长=圆的周长+半径×2,圆的周长=πd,据此解答。
【详解】3.14×1×2+1×2
=6.28+2
=8.28(厘米)
故选择:C
【点睛】明确长方形比圆的周长多两个半径的长度,掌握圆的周长计算公式是解题关键。
6.C
【分析】根据圆的周长公式:周长=π×2×半径,代入数据,求出这个圆的周长,再除以2,求出圆周长的一半,再加上这个半圆的直径,就是这个半圆的周长,据此解答。
【详解】3.14×2×5÷2+5×2
=6.28×5÷2+10
=31.4÷2+10
=15.7+10
=25.7(厘米)
故答案为:C
【点睛】解答本题的关键是熟记圆柱的周长公式,关键明确半圆的周长需要加上半圆的直径。
7. 18.84 28.26
【分析】根据题意可知,剪拼成的长方形的长就是圆周长的一半,据此求出圆的周长;再根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,求出半径;再根据圆的面积公式:π×半径2;代入数据,即可解答。
【详解】9.42×2=18.18(厘米)
18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
【点睛】熟练掌握圆的面积公式推导过程是解答本题的关键。
8. 6 28.26
【详解】略
9.15.7
【解析】略
10.5.375
【分析】根据图形可知,阴影部分面积=边长是5厘米的正方形面积-半径是(5÷2)的圆的面积,根据正方形面积公式:边长×边长;圆的面积公式:π×半径2,代入数据,即可解答。
【详解】5×5-3.14×(5÷2)2
=25-3.14×2.52
=25-3.14×6.25
=25-19.625
=5.375(平方厘米)
【点睛】利用长方形面积公式和圆的面积公式进行解答。
11. 4 20.56
【分析】在长8厘米、宽6厘米的长方形中画一个最大的半圆,半圆直径是这个长方形的长,则半圆的半径=直径÷2;根据半圆周长=圆周长的一半+直径。
【详解】8÷2=4(厘米)
周长:3.14×8÷2+8
=12.56+8
=20.56(厘米)
【点睛】关键是确定圆的直径是解题的关键,同时要注意半圆的周长是圆的周长一半加上直径的长度。
12.28.26
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,面积不变,拼成的长方形的长等于圆周长的一半,宽等于圆的半径,已知拼成的长方形的周长比圆的周长增加6厘米,也就是增加了2个半径,据此可以求出圆的半径,再根据圆的面积公式:S=πr2,求出圆的面积。
【详解】3.14×(6÷2)2
=3.14×9
=28.26()
【点睛】本题主要考查圆的面积公式的灵活运用,关键是熟记公式。
13. 18.84 28.26
【分析】根据圆形的周长公式:C=2πr,面积公式:S=πr2,将数据代入计算即可。
【详解】周长:
2×3×3.14
=6×3.14
=18.84(米)
面积:
3.14×32
=3.14×9
=28.26(平方米)
体育老师用一根绳在操场上画了一个半径为3米的圆,这个圆周长是18.84米,占地面积是28.26平方米。
【点睛】此题考查了圆的周长与面积计算,关键能够熟记公式。
14. 21 9.42
【分析】通过观察图形可知,长方形的长等于圆直径的2.5倍,宽等于圆的直径,根据长方形的周长=(长+宽)×2,圆的周长公式:C=πd,把数据代入公式解答。
【详解】(3×2.5+3)×2
=(7.5+3)×2
=10.5×2
=21(厘米)
3.14×3=9.42(厘米)
长方形的周长是21厘米,一个圆的周长是9.42厘米。
【点睛】此题主要考查长方形的周长公式、圆的周长公式的灵活运用,关键是熟记公式。
15.√
【分析】根据圆的周长公式C=2πr代入数据,即可判断。
【详解】2×3.14×10
=3.14×20
=62.8(cm)
一个圆的半径是10cm,这个圆的周长是62.8cm,此说法正确。
故答案为:√
【点睛】此题主要考查了圆的周长计算公式。
16.√
【解析】略
17.√
【分析】根据公式圆的周长C=2πr,半径相等,2和π为定值,所以半径相等周长一定相等,据此解答。
【详解】根据分析可得,两个圆的半径相等,这两个圆的周长也一定相等。原题说法正确;
故答案为:√。
【点睛】本题考查了圆的周长定义,圆的周长与半径和直径有关,半径或直径相等的圆周长一定相等。
18.×
【分析】圆周率是圆的周长与直径的比值,是一个固定不变的数,不随直径的变化而变化,据此判断即可。
【详解】圆周率=圆的周长÷直径,因为圆周率是一个定值,所以周长一定时,直径也一定,故原题说法错误。
故答案为:×
【点睛】本题考查对圆周率的认识,需掌握圆周率的定义。
19.√
【分析】两个端点都在圆上的线段中,经过圆心的线段最长,也就是圆的直径。
【详解】在同一个圆中,两个端点都在圆上的线段中,直径最长。原题说法正确。
故答案为:√
【点睛】此题考查的是圆的有关知识的理解,圆内所有的线段中,直径最长。
20.
【分析】从图上可得:用梯形的面积减去半圆的面积,即可得出答案。半圆的半径是,所以梯形的上底是,又因为这是一个直角梯形,所以梯形的高等于半圆的半径。将数据代入梯形面积公式(上底下底)高和半圆的面积公式,即可得出答案。
【详解】(6+9)×6÷2-×3.14×62
=15×6÷2-0.785×36
=90÷2-28.26
=45-28.26
=16.74(cm2)
阴影部分的面积是16.74 cm2。
21.19.74平方厘米
【分析】通过观察图形可知,涂色部分的面积等于长方形的面积减去圆的面积,根据长方形的面积公式:S=ab,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】8×6-3.14×(6÷2)2
=48-3.14×9
=48-28.26
=19.74(平方厘米)
涂色部分的面积是19.74平方厘米。
22.如图
【详解】试题分析:(1)圆心确定圆的位置,半径确定圆的大小,由此以点O为圆心,以3÷2=1.5厘米为半径画圆;
(2)圆的对称轴有无数条,分别是经过圆心的直线,由此经过圆心画出两条互相垂直的直线即可.
解:以点O为圆心,以3÷2=1.5厘米为半径画圆,并画出它的互相垂直的两条对称轴如图所示:
点评:此题考查了利用圆的两大要素:圆心与半径画圆的方法,以及利用轴对称图形的定义确定圆的对称轴位置的方法的灵活应用.
23.31.4分米
【详解】3.14×10=31.4(分米)
24.如图,剩下的纸板的面积是14.88平方厘米
【详解】试题分析:(1)根据长方形内最大的半圆的半径特点可知:这个半圆的半径是4厘米,由此即可在图中画出这个半圆,
(2)剩下的纸板料的面积就等于长方形的面积减去半圆的面积,由此利用长方形和圆的面积公式即可解答.
解:(1)观察图形可知,半圆的半径是4厘米,由此以长方形的一条长的中点为圆心,以4厘米为半径,在这个长方形纸板上画出这个半圆如图所示:
;
(2)10×4﹣3.14×42÷2,
=40﹣25.12,
=14.88(平方厘米),
答:剩下的纸板的面积是14.88平方厘米.
点评:此题考查了长方形内最大的半圆的画法以及长方形与圆的面积公式的灵活应用.
25.40秒
【分析】先求出轮胎的周长,根据圆的周长公式:,再用轮胎的周长×5圈,求出1秒钟轮胎转多少米,再用大桥的长度除以轮胎一秒钟转的米数,即可解答。
【详解】15分米=1.5米
942÷(3.14×1.5×5)
=942÷(4.71×5)
=942÷23.55
=40(秒)
答:需要40秒。
【点睛】本题考查圆的周长公式的应用,关键是熟记公式,注意单位名数的统一。
26.172.7平方厘米
【分析】根据题意,求这块玉璧的正面的面积,就是求圆环的面积,根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,即可解答。
【详解】内圆的半径:6÷2=3(厘米)
3.14×(82-32)
=3.14×(64-9)
=3.14×55
=172.7(平方厘米)
答:这块玉璧正面的面积是172.7平方厘米。
【点睛】熟练掌握圆环的面积公式是解答本题的关键。
27.28.26平方米;141只
【分析】观察图形可知,养鸡场的面积是圆的面积的;已知圆周长的的长度,根据圆的周长公式:周长=π×2×半径;半径=周长÷2÷π;代入数据,求出这个圆的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出这个圆的面积,再除以4,即可求出这个养鸡场的面积;再用养鸡场的面积÷每只鸡占地面积,即可解答。
【详解】9.42×4÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
3.14×62÷4
=3.14×36÷4
=113.04÷4
=28.26(平方米)
28.26÷0.2≈141(只)
答:这个养鸡场的面积是28.26平方米;这个养鸡场最多可以养141只鸡。
【点睛】利用圆的周长公式、面积公式进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
