辽宁省沈阳市辽中区第二高级中学2022-2023学年高一下学期4月月考数学试题(Word版含答案)
文档属性
| 名称 | 辽宁省沈阳市辽中区第二高级中学2022-2023学年高一下学期4月月考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 835.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 16:10:57 | ||
图片预览



文档简介
沈阳市辽中区第二高级中学2022-2023学年高一下学期4月月考
数学
一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.第一承限角一定是锐角 B.终边相同角一定相等
C.小于90°的角一定是锐角 D.钝角的终边在第二象限
2.在半径为5cm的扇形中,圆心角为2rad,则扇形面积为( )
A.25cm B.10cm C. D.
3.若向量,,若与所成角为锐角,则n的取值范围是( )
A. B.且
C. D.且
4.要想得到函数的图像,只需要将函数的图像上的所有点( )
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D.向左平移个单位
5.函数在区间内应为( )
A. B.
C. D.
6.平面向量与互相垂直,已知,,且与向量的夹角是钝角,则( )
A. B. C. D.
7.设函数,则下列结论错误的是( )
A.的周期为 B.的图像关于直线对称
C.的一个零点为 D.在上单调递减
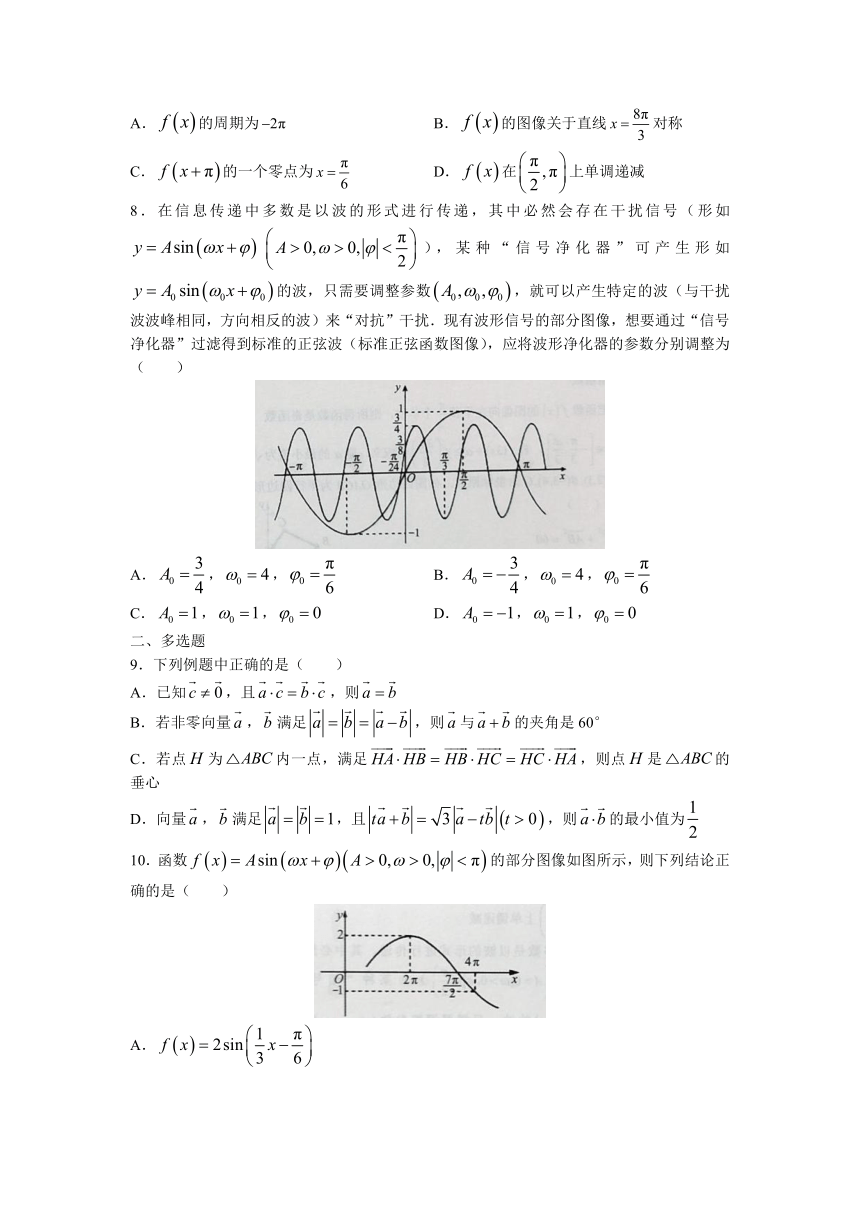
8.在信息传递中多数是以波的形式进行传递,其中必然会存在干扰信号(形如),某种“信号净化器”可产生形如的波,只需要调整参数,就可以产生特定的波(与干扰波波峰相同,方向相反的波)来“对抗”干扰.现有波形信号的部分图像,想要通过“信号净化器”过滤得到标准的正弦波(标准正弦函数图像),应将波形净化器的参数分别调整为( )
A.,, B.,,
C.,, D.,,
二、多选题
9.下列例题中正确的是( )
A.已知,且,则
B.若非零向量,满足,则与的夹角是60°
C.若点为内一点,满足,则点是的垂心
D.向量,满足,且,则的最小值为
10.函数的部分图像如图所示,则下列结论正确的是( )
A.
B.若把的横坐标缩短为原来的倍,纵坐标不变,得到的函数在上增函数
C.若把函数的图像向左平移个单位,则所得函数是奇函数
D.,若恒成立,则的最小值为
11.已知,,为坐标原点,如图四边形为平行四边形,下列结论正确的是( )
A. B.在上的投影的数量为
C. D.的重心坐标为
12.2023年1月出版的《中国高考报告2023》中指出,高考数学试题将会全面的加入复杂情境,更加注重数学思维能力和思想方法的考察,考故难度加大。某教师从“丢手绢”游戏中抽象出以下数学问题,质点和在以坐标原点为圆心,半径为l的上逆时针匀速圆周运动,同时出发,的角速度大小为,起点为与x轴正半轴的交点;Q的角速度大小为5rad/s,起点为射线与的交点,则当与重合时,的坐标可以为( )
A. B.
C. D.
三、填空题
13.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边上有一点,且,则的值为______.
14.已知函数,则函数的定义域为______.
15.已知中,,,是边的中点,为所在平面内一点,若是边长为2的等边三角形,则的值为______.
16.函数的图像与函数的图像在上有交点的横坐标之和为______.
17.已知
(1)化简.
(2)若为第三象限角,且,求的值.
18.已知.
(1)求的值;
(2)若,求的值.
19.已知点的平面直角坐标系中的坐标为,平面向量,,且,,.
(1)求实数,及点的坐标;
(2)求向量与向量夹角的余弦值.
20.已知函数在一个周期的图像上有相邻的最高点和最低点.
(1)求,,的值;
(2)设函数当时,总存在两个零点,求实数的取值范围.
21.已知,,函数的最小值为.
(1)求;
(2)若,求及此时的最大值.
22.已知函数的振幅为1,函数在区间单调,且.
(1)求图像的一条对称轴;
(2)若,求初相.
沈阳市辽中区第二高级中学2022-2023学年高一下学期4月月考
数学参考答案及评分标准
一、单选题:本题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 D C B A D A D B
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的给5分,部分选对的给2分,有选错的给0分;
题号 9 10 11 12
答案 CD ACD ABC ABD
三、填空题:本题共4小题,每小题5分共20分
13.0或 14.
15.或 16.5
四、解答题:
17.(1)
.
(2)∵为第三象限角,且,
∴,.
此题每一小问5分,步骤的给分情况批卷老师可以根据学生对诱导公式举握情况酌情给分
18.解:(1)由已知得,∴.
(2)∵,
∴,
又∵,∴,,∴
∴,∴原式.
19.解:(1),∴,,
所以,因为,
所以
所以;
(2)由(1)可知
,
∴;
20.解:(1)由函数在一个周期的图泉上有相邻的最高点和最低点.
知,,所以,.
∴,∵在函数上
∴,∴
∵,∴,∴,,
(2)由(1),
∴
∴当时有两解,∵,∴
∴,∴
∴实数m取值范围为;
21.解(1)由
.
这里.
①当时,;
②当,时,;
③当,时,.
因此,,
(2),
①若,则有,得,矛盾;
②若,则有,
即,∴或(舍),
∴时,.
此时,,当时,取得最大值5.
22.(1)∵振幅为1,∴
∵,∴即,∴,∵,∴
∵,∴的一条对称轴方程为
(2)∵
∴或,
∵为对称轴,∴,
若
②-①得:
∴,且所以没有值使得上式成立.
若
④-③得:
∴,∴时,
此时,,∵,∴即初相为.
数学
一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.第一承限角一定是锐角 B.终边相同角一定相等
C.小于90°的角一定是锐角 D.钝角的终边在第二象限
2.在半径为5cm的扇形中,圆心角为2rad,则扇形面积为( )
A.25cm B.10cm C. D.
3.若向量,,若与所成角为锐角,则n的取值范围是( )
A. B.且
C. D.且
4.要想得到函数的图像,只需要将函数的图像上的所有点( )
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D.向左平移个单位
5.函数在区间内应为( )
A. B.
C. D.
6.平面向量与互相垂直,已知,,且与向量的夹角是钝角,则( )
A. B. C. D.
7.设函数,则下列结论错误的是( )
A.的周期为 B.的图像关于直线对称
C.的一个零点为 D.在上单调递减
8.在信息传递中多数是以波的形式进行传递,其中必然会存在干扰信号(形如),某种“信号净化器”可产生形如的波,只需要调整参数,就可以产生特定的波(与干扰波波峰相同,方向相反的波)来“对抗”干扰.现有波形信号的部分图像,想要通过“信号净化器”过滤得到标准的正弦波(标准正弦函数图像),应将波形净化器的参数分别调整为( )
A.,, B.,,
C.,, D.,,
二、多选题
9.下列例题中正确的是( )
A.已知,且,则
B.若非零向量,满足,则与的夹角是60°
C.若点为内一点,满足,则点是的垂心
D.向量,满足,且,则的最小值为
10.函数的部分图像如图所示,则下列结论正确的是( )
A.
B.若把的横坐标缩短为原来的倍,纵坐标不变,得到的函数在上增函数
C.若把函数的图像向左平移个单位,则所得函数是奇函数
D.,若恒成立,则的最小值为
11.已知,,为坐标原点,如图四边形为平行四边形,下列结论正确的是( )
A. B.在上的投影的数量为
C. D.的重心坐标为
12.2023年1月出版的《中国高考报告2023》中指出,高考数学试题将会全面的加入复杂情境,更加注重数学思维能力和思想方法的考察,考故难度加大。某教师从“丢手绢”游戏中抽象出以下数学问题,质点和在以坐标原点为圆心,半径为l的上逆时针匀速圆周运动,同时出发,的角速度大小为,起点为与x轴正半轴的交点;Q的角速度大小为5rad/s,起点为射线与的交点,则当与重合时,的坐标可以为( )
A. B.
C. D.
三、填空题
13.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边上有一点,且,则的值为______.
14.已知函数,则函数的定义域为______.
15.已知中,,,是边的中点,为所在平面内一点,若是边长为2的等边三角形,则的值为______.
16.函数的图像与函数的图像在上有交点的横坐标之和为______.
17.已知
(1)化简.
(2)若为第三象限角,且,求的值.
18.已知.
(1)求的值;
(2)若,求的值.
19.已知点的平面直角坐标系中的坐标为,平面向量,,且,,.
(1)求实数,及点的坐标;
(2)求向量与向量夹角的余弦值.
20.已知函数在一个周期的图像上有相邻的最高点和最低点.
(1)求,,的值;
(2)设函数当时,总存在两个零点,求实数的取值范围.
21.已知,,函数的最小值为.
(1)求;
(2)若,求及此时的最大值.
22.已知函数的振幅为1,函数在区间单调,且.
(1)求图像的一条对称轴;
(2)若,求初相.
沈阳市辽中区第二高级中学2022-2023学年高一下学期4月月考
数学参考答案及评分标准
一、单选题:本题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 D C B A D A D B
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的给5分,部分选对的给2分,有选错的给0分;
题号 9 10 11 12
答案 CD ACD ABC ABD
三、填空题:本题共4小题,每小题5分共20分
13.0或 14.
15.或 16.5
四、解答题:
17.(1)
.
(2)∵为第三象限角,且,
∴,.
此题每一小问5分,步骤的给分情况批卷老师可以根据学生对诱导公式举握情况酌情给分
18.解:(1)由已知得,∴.
(2)∵,
∴,
又∵,∴,,∴
∴,∴原式.
19.解:(1),∴,,
所以,因为,
所以
所以;
(2)由(1)可知
,
∴;
20.解:(1)由函数在一个周期的图泉上有相邻的最高点和最低点.
知,,所以,.
∴,∵在函数上
∴,∴
∵,∴,∴,,
(2)由(1),
∴
∴当时有两解,∵,∴
∴,∴
∴实数m取值范围为;
21.解(1)由
.
这里.
①当时,;
②当,时,;
③当,时,.
因此,,
(2),
①若,则有,得,矛盾;
②若,则有,
即,∴或(舍),
∴时,.
此时,,当时,取得最大值5.
22.(1)∵振幅为1,∴
∵,∴即,∴,∵,∴
∵,∴的一条对称轴方程为
(2)∵
∴或,
∵为对称轴,∴,
若
②-①得:
∴,且所以没有值使得上式成立.
若
④-③得:
∴,∴时,
此时,,∵,∴即初相为.
同课章节目录
