重庆市重点高中2022-2023学年高二下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 重庆市重点高中2022-2023学年高二下学期期中考试数学试题(Word版含答案) | 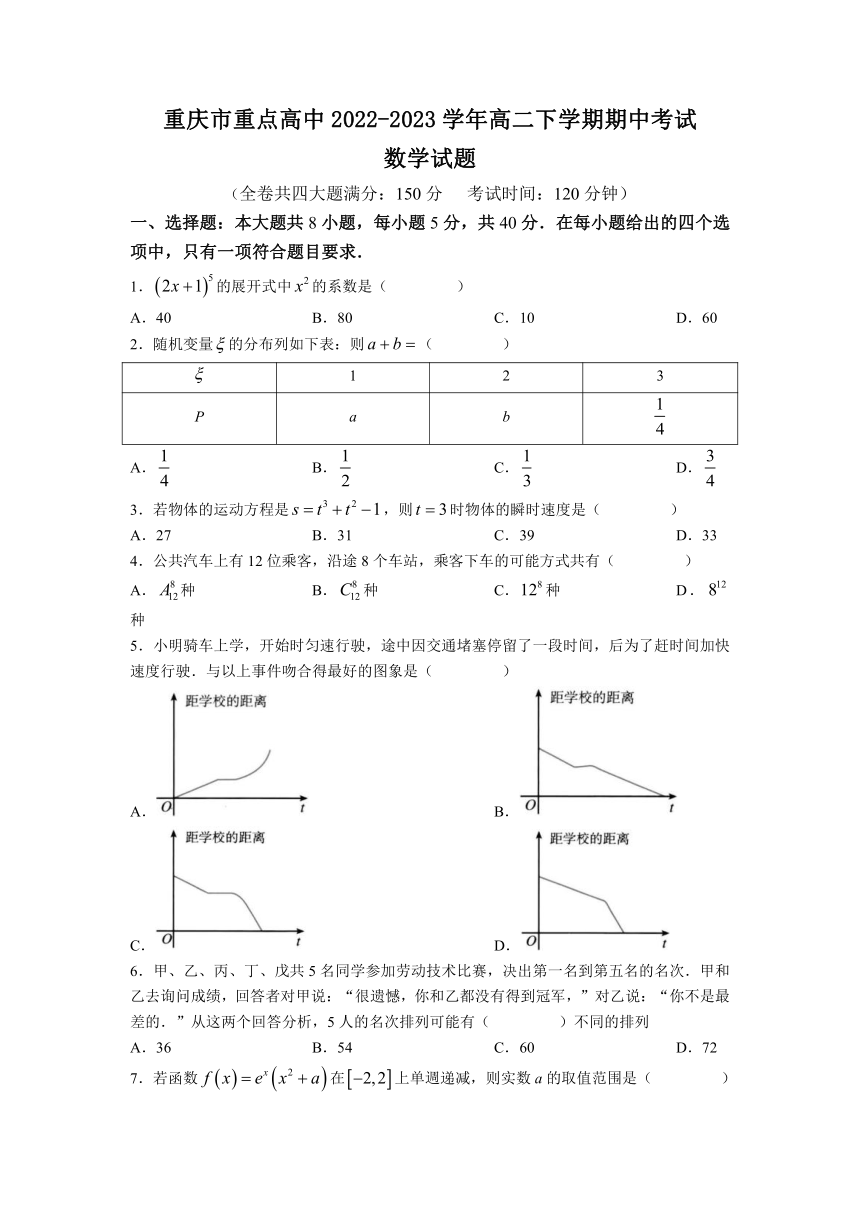 | |
| 格式 | doc | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 16:07:51 | ||
图片预览



文档简介
重庆市重点高中2022-2023学年高二下学期期中考试
数学试题
(全卷共四大题满分:150分 考试时间:120分钟)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1.的展开式中的系数是( )
A.40 B.80 C.10 D.60
2.随机变量的分布列如下表:则( )
1 2 3
P a b
A. B. C. D.
3.若物体的运动方程是,则时物体的瞬时速度是( )
A.27 B.31 C.39 D.33
4.公共汽车上有12位乘客,沿途8个车站,乘客下车的可能方式共有( )
A.种 B.种 C.种 D.种
5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
A. B.
C. D.
6.甲、乙、丙、丁、戊共5名同学参加劳动技术比赛,决出第一名到第五名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军,”对乙说:“你不是最差的.”从这两个回答分析,5人的名次排列可能有( )不同的排列
A.36 B.54 C.60 D.72
7.若函数在上单週递减,则实数a的取值范围是( )
A. B. C. D.
8.已知函数,若存在唯一的零点,且,则a的取值范围是( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.关于的展开式,下列结论正确的是( )
A.二项式系数和为64 B.所有项的系数之和为2
C.第三项的二项式系数最大 D.项的系数为240
10.已知A,B是两个随机事件,,下列命题正确的是( )
A.若A,B相互独立, B.若,则
C.若A,B是对立事件,则 D.若A,B是互斥事件,则
11.若方程有两个不相等的实数根,实数a的取值可以是( )
A.0 B. C. D.1
12.甲、乙、丙三人相互做传球训练,第一次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,下列说法正确的是( )
A.2次传球后球在丙手上的概率是 B.3次传球后球在乙手上的概率是
C.3次传球后球在甲手上的概率是 D.n次传球后球在甲手上的概率是
三、填空题:本题共4小题,每小题5分,共20分.
13.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(请用数字作答)
14.曲线在点处的切线方程为 .
15.的展开式中项系数为 .
16.已知,分别是函数的极小值点和极大值点.若,则a的取值范围是 .
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知中,且.
(1)求m的值;
(2)求的值.
18.已知,曲线在点处的切线斜率为5.
(1)求a的值;
(2)求函数的极值.
19.彭老师要从10篇课文中随机抽3篇不同的课文让同学背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的7篇,求:
(1)抽到他能背诵的课文的数量X的分布列;
(2)他能及格的概率.
20.已知函数v.
(1)讨论函数的单调性;
(2)若对任意的,恒成立,求实数a的取值范围.
21.在一次数学随堂小测验中,有单项选择题和多项选择题两种.单项选择题,每道题四个选项中仅有一个正确,选择正确得5分,选择错误得0分;多项选择题,每道题四个选项中有两个或三个选项正确,全部选对得5分,部分选对得2分,有选择错误的得0分.
(1)小明同学在这次测验中,如果不知道单项选择题的答案就随机猜测.已知小明知道单项选择题的正确答案和随机猜测的概率都是.问小明在做某道单项选择题时,在该道题做对的条件下,求他知道这道单项选择题正确答案的概率.
(2)小明同学在做多选题时,选择一个选项的概率为,选择两个选项的概率为,选择三个选项的概率为.已知某个多项选择题有三个选项是正确的,小明在完全不知道四个选项正误的情况下,只好根据自己的经验随机选择,求小明做这道多项选择题得5分或2分的概率.
22.已知函数.
(1)若在单调递增,求实数a的取值范围;
(2)若函数有两个极值点,,且,求证:.
重庆市重点高中2022-2023学年高二下学期期中考试
数学试题答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 A D D D C B C C
二、多项选择题
题号 9 10 11 12
答案 AD ABD BC ACD
三、填空题
题号 13 14 15 16
答案 16 -60
17.
(1)m= 2
(2)
18.
(1)a=2
(2)极大值为-3,无极小值
19.
(1)分布列如下:
X 0 1 2 3
P
(2)他能及格的概率为
20.
(1)依题意,,
当时,显然,所以在上单调递增;
当时,令,得;令,;
即在上单调递增,在上单调递减.
(2)由题意得恒成立,
等价于恒成立,
令,即时成立.
则,
当时,,
当时,,
那么在上单调递增,在上单调递增减,
所以,
所以.
21.
(1)记事件A为“该单项选择题回答正确”,事件B为“小明直到该题的正确答案”,
∵,
∴,
即小明在做某道单项选择题时,在该道题做对的条件下,他知道这道单项选择题正确答案的概率为.
(2)设事件表示小明选择了i个选项,事件C表示选择的选项是正确的,
∴;
;
小明做这道多项选择题得5分或2分的概率为
22.
(1)解:的定义域为,,
若单调递增,则在上恒成立,
即在上恒成立,
在上单调递减,于是,
所以,
所以实数a的取值范围为;
(2)证明:,
,
依题意可得,是方程的两个不同的根,
于是,且.
要证,
只需证,
即证,,
因为,
所以,
从而
,
令,,
则,
设,
则,
令,
解得(舍去),
由,得,
由,得,
于是在上单调递增,在上单调递减,
即在上单调递增,在上单调递减,
而,,于是在上,,
因此在上单调递增,
从而,
综上所述,,
所以原命题获证.
数学试题
(全卷共四大题满分:150分 考试时间:120分钟)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1.的展开式中的系数是( )
A.40 B.80 C.10 D.60
2.随机变量的分布列如下表:则( )
1 2 3
P a b
A. B. C. D.
3.若物体的运动方程是,则时物体的瞬时速度是( )
A.27 B.31 C.39 D.33
4.公共汽车上有12位乘客,沿途8个车站,乘客下车的可能方式共有( )
A.种 B.种 C.种 D.种
5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
A. B.
C. D.
6.甲、乙、丙、丁、戊共5名同学参加劳动技术比赛,决出第一名到第五名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军,”对乙说:“你不是最差的.”从这两个回答分析,5人的名次排列可能有( )不同的排列
A.36 B.54 C.60 D.72
7.若函数在上单週递减,则实数a的取值范围是( )
A. B. C. D.
8.已知函数,若存在唯一的零点,且,则a的取值范围是( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.关于的展开式,下列结论正确的是( )
A.二项式系数和为64 B.所有项的系数之和为2
C.第三项的二项式系数最大 D.项的系数为240
10.已知A,B是两个随机事件,,下列命题正确的是( )
A.若A,B相互独立, B.若,则
C.若A,B是对立事件,则 D.若A,B是互斥事件,则
11.若方程有两个不相等的实数根,实数a的取值可以是( )
A.0 B. C. D.1
12.甲、乙、丙三人相互做传球训练,第一次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,下列说法正确的是( )
A.2次传球后球在丙手上的概率是 B.3次传球后球在乙手上的概率是
C.3次传球后球在甲手上的概率是 D.n次传球后球在甲手上的概率是
三、填空题:本题共4小题,每小题5分,共20分.
13.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(请用数字作答)
14.曲线在点处的切线方程为 .
15.的展开式中项系数为 .
16.已知,分别是函数的极小值点和极大值点.若,则a的取值范围是 .
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知中,且.
(1)求m的值;
(2)求的值.
18.已知,曲线在点处的切线斜率为5.
(1)求a的值;
(2)求函数的极值.
19.彭老师要从10篇课文中随机抽3篇不同的课文让同学背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的7篇,求:
(1)抽到他能背诵的课文的数量X的分布列;
(2)他能及格的概率.
20.已知函数v.
(1)讨论函数的单调性;
(2)若对任意的,恒成立,求实数a的取值范围.
21.在一次数学随堂小测验中,有单项选择题和多项选择题两种.单项选择题,每道题四个选项中仅有一个正确,选择正确得5分,选择错误得0分;多项选择题,每道题四个选项中有两个或三个选项正确,全部选对得5分,部分选对得2分,有选择错误的得0分.
(1)小明同学在这次测验中,如果不知道单项选择题的答案就随机猜测.已知小明知道单项选择题的正确答案和随机猜测的概率都是.问小明在做某道单项选择题时,在该道题做对的条件下,求他知道这道单项选择题正确答案的概率.
(2)小明同学在做多选题时,选择一个选项的概率为,选择两个选项的概率为,选择三个选项的概率为.已知某个多项选择题有三个选项是正确的,小明在完全不知道四个选项正误的情况下,只好根据自己的经验随机选择,求小明做这道多项选择题得5分或2分的概率.
22.已知函数.
(1)若在单调递增,求实数a的取值范围;
(2)若函数有两个极值点,,且,求证:.
重庆市重点高中2022-2023学年高二下学期期中考试
数学试题答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 A D D D C B C C
二、多项选择题
题号 9 10 11 12
答案 AD ABD BC ACD
三、填空题
题号 13 14 15 16
答案 16 -60
17.
(1)m= 2
(2)
18.
(1)a=2
(2)极大值为-3,无极小值
19.
(1)分布列如下:
X 0 1 2 3
P
(2)他能及格的概率为
20.
(1)依题意,,
当时,显然,所以在上单调递增;
当时,令,得;令,;
即在上单调递增,在上单调递减.
(2)由题意得恒成立,
等价于恒成立,
令,即时成立.
则,
当时,,
当时,,
那么在上单调递增,在上单调递增减,
所以,
所以.
21.
(1)记事件A为“该单项选择题回答正确”,事件B为“小明直到该题的正确答案”,
∵,
∴,
即小明在做某道单项选择题时,在该道题做对的条件下,他知道这道单项选择题正确答案的概率为.
(2)设事件表示小明选择了i个选项,事件C表示选择的选项是正确的,
∴;
;
小明做这道多项选择题得5分或2分的概率为
22.
(1)解:的定义域为,,
若单调递增,则在上恒成立,
即在上恒成立,
在上单调递减,于是,
所以,
所以实数a的取值范围为;
(2)证明:,
,
依题意可得,是方程的两个不同的根,
于是,且.
要证,
只需证,
即证,,
因为,
所以,
从而
,
令,,
则,
设,
则,
令,
解得(舍去),
由,得,
由,得,
于是在上单调递增,在上单调递减,
即在上单调递增,在上单调递减,
而,,于是在上,,
因此在上单调递增,
从而,
综上所述,,
所以原命题获证.
同课章节目录
