-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册8.3.2独立性检验+课件(共24张)
文档属性
| 名称 | -2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册8.3.2独立性检验+课件(共24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 16:40:17 | ||
图片预览





文档简介
(共24张PPT)
第八章成对数据的统计分析
8.3.2 独立性检验
一个2×2列联表如下:
则表中m,n的值分别是( )
A.10,38 B.17,45
C.10,45 D.17,38
X Y 合计
Y=y1 Y=y2
X=x1 a 35 45
X=x2 7 b n
合计 m 73 s
B
复习回顾
χ2=
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2
这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作卡方独立性检验,简称独立性检验.
新知讲解
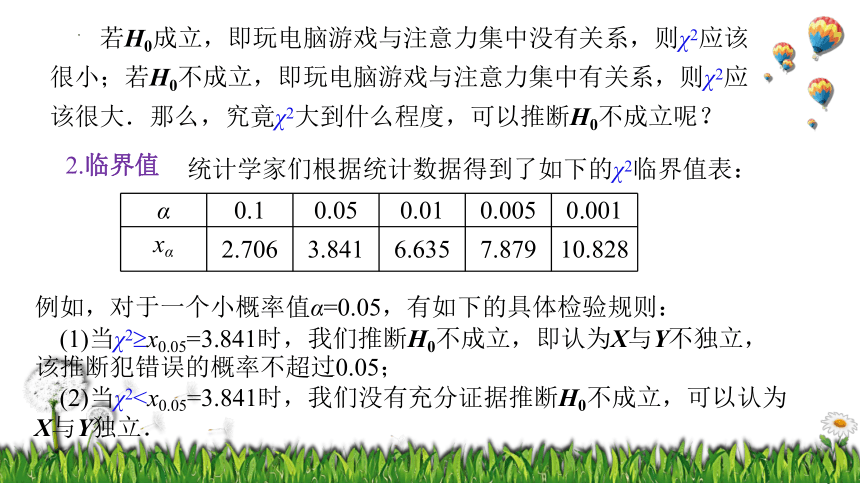
若H0成立,即玩电脑游戏与注意力集中没有关系,则χ2应该很小;若H0不成立,即玩电脑游戏与注意力集中有关系,则χ2应该很大.那么,究竟χ2大到什么程度,可以推断H0不成立呢?
2.临界值
统计学家们根据统计数据得到了如下的χ2临界值表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
例如,对于一个小概率值α=0.05,有如下的具体检验规则:
(1)当χ2 x0.05=3.841时,我们推断H0不成立,即认为X与Y不独立,该推断犯错误的概率不超过0.05;
(2)当χ2 x0.05=3.841时,我们没有充分证据推断H0不成立,可以认为X与Y独立.
1. 小概率值α的临界值:
忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2 ≥xα)=α成立. 我们称xα为α的临界值,这个临界值就可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
2. χ2计算公式:
3. 基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ2知识总结
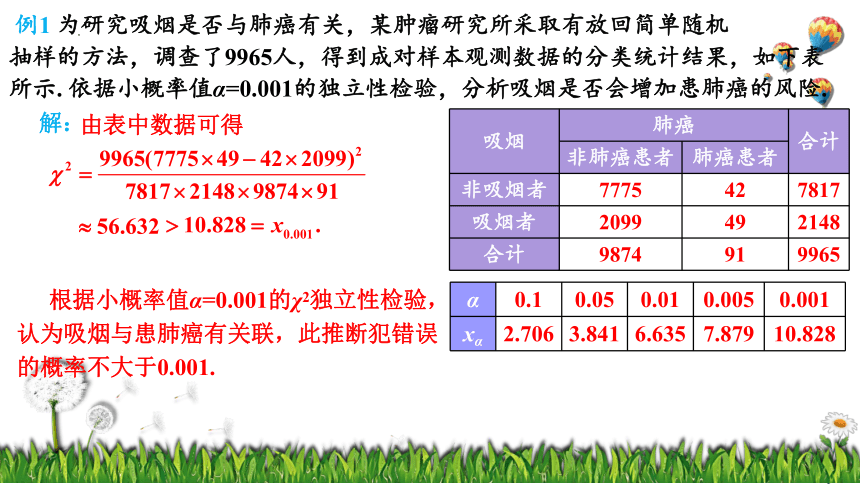
由表中数据可得
例1 为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机
抽样的方法,调查了9965人,得到成对样本观测数据的分类统计结果,如下表所示. 依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险.
解:
吸烟 肺癌 合计
非肺癌患者 肺癌患者
非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
根据小概率值α=0.001的χ2独立性检验,认为吸烟与患肺癌有关联,此推断犯错误的概率不大于0.001.
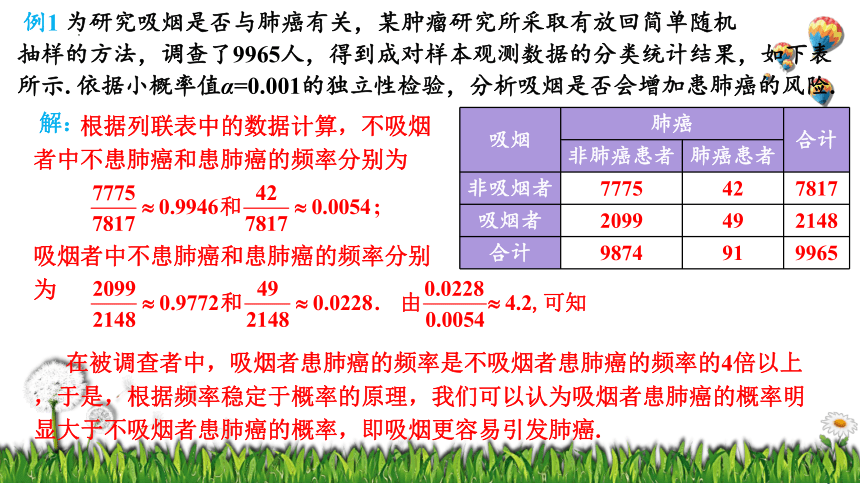
例1 为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机
抽样的方法,调查了9965人,得到成对样本观测数据的分类统计结果,如下表所示. 依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险.
解:
吸烟 肺癌 合计
非肺癌患者 肺癌患者
非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
根据列联表中的数据计算,不吸烟者中不患肺癌和患肺癌的频率分别为
吸烟者中不患肺癌和患肺癌的频率分别为
在被调查者中,吸烟者患肺癌的频率是不吸烟者患肺癌的频率的4倍以上,于是,根据频率稳定于概率的原理,我们可以认为吸烟者患肺癌的概率明显大于不吸烟者患肺癌的概率,即吸烟更容易引发肺癌.
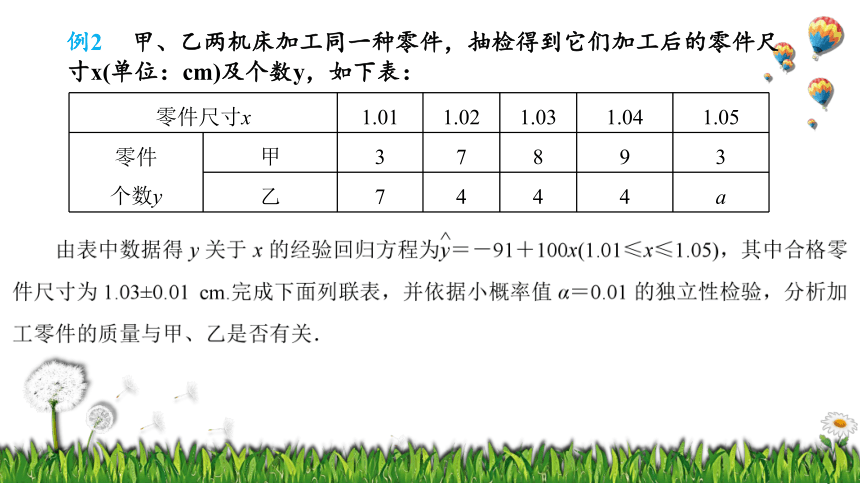
例2 甲、乙两机床加工同一种零件,抽检得到它们加工后的零件尺寸x(单位:cm)及个数y,如下表:
零件尺寸x 1.01 1.02 1.03 1.04 1.05
零件 个数y 甲 3 7 8 9 3
乙 7 4 4 4 a
机床加工 零件的质量 合计
合格零件数 不合格零件数
甲
乙
合计
例题讲解
例题讲解
例题讲解
例题讲解
方法技巧
方法技巧
1.打鼾不仅影响别人休息,而且可能与患心脏病有关.下表是一次调查所得的数据:
根据小概率值α=0.001的独立性检验,能否认为每一晚都打鼾与患心脏病有关系?
打鼾 心脏病 合计
患病 未患病
每一晚都打鼾 30 224 254
不打鼾 24 1355 1379
合计 54 1579 1633
巩固练习
巩固练习
1.某省进行高中新课程改革,为了解教师对新课程教学模式的使用情况,某一教育机构对某学校的教师关于新课程教学模式的使用情况进行了问卷调查,共调查了50人,其中有老教师20人,青年教师30人.老教师对新课程教学模式赞同的有10人,不赞同的有10人;青年教师对新课程教学模式赞同的有24人,不赞同的有6人.
(1)根据以上数据建立一个2×2列联表;
(2)试根据小概率值α=0.01的独立性检验,分析对新课程教学模式的赞同情况与教师年龄是否有关系.
巩固练习
解:(1)2×2列联表如表所示:
教师年龄 对新课程教学模式 合计
赞同 不赞同
老教师 10 10 20
青年教师 24 6 30
合计 34 16 50
巩固练习
巩固练习
独立性检验的关注点
(1)步骤:列表,计算,判断;
(2)注意:①χ2计算公式较复杂,一是公式要清楚;二是代入数值时不能张冠李戴;三是计算时要细心;
②判断时把计算结果与临界值比较,其值越大,有关的可信度越高.
方法技巧
方法技巧
3. 学校举行运动会,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下2×2列联表:
运动的喜好 合计
喜爱运动 不喜爱运动
男 10 16
女 6 14
合计 30
巩固练习
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
解:(1)
运动的喜好 合计
喜爱运动 不喜爱运动
男 10 6 16
女 6 8 14
合计 16 14 30
巩固练习
巩固练习
1. 小概率值α的临界值:
忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2 ≥xα)=α成立. 我们称xα为α的临界值,这个临界值就可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
2. χ2计算公式:
3. 基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ2课堂小结
谢 谢 !
第八章成对数据的统计分析
8.3.2 独立性检验
一个2×2列联表如下:
则表中m,n的值分别是( )
A.10,38 B.17,45
C.10,45 D.17,38
X Y 合计
Y=y1 Y=y2
X=x1 a 35 45
X=x2 7 b n
合计 m 73 s
B
复习回顾
χ2=
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2
这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作卡方独立性检验,简称独立性检验.
新知讲解
若H0成立,即玩电脑游戏与注意力集中没有关系,则χ2应该很小;若H0不成立,即玩电脑游戏与注意力集中有关系,则χ2应该很大.那么,究竟χ2大到什么程度,可以推断H0不成立呢?
2.临界值
统计学家们根据统计数据得到了如下的χ2临界值表:
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
例如,对于一个小概率值α=0.05,有如下的具体检验规则:
(1)当χ2 x0.05=3.841时,我们推断H0不成立,即认为X与Y不独立,该推断犯错误的概率不超过0.05;
(2)当χ2 x0.05=3.841时,我们没有充分证据推断H0不成立,可以认为X与Y独立.
1. 小概率值α的临界值:
忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2 ≥xα)=α成立. 我们称xα为α的临界值,这个临界值就可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
2. χ2计算公式:
3. 基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ2
由表中数据可得
例1 为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机
抽样的方法,调查了9965人,得到成对样本观测数据的分类统计结果,如下表所示. 依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险.
解:
吸烟 肺癌 合计
非肺癌患者 肺癌患者
非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
根据小概率值α=0.001的χ2独立性检验,认为吸烟与患肺癌有关联,此推断犯错误的概率不大于0.001.
例1 为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机
抽样的方法,调查了9965人,得到成对样本观测数据的分类统计结果,如下表所示. 依据小概率值α=0.001的独立性检验,分析吸烟是否会增加患肺癌的风险.
解:
吸烟 肺癌 合计
非肺癌患者 肺癌患者
非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
根据列联表中的数据计算,不吸烟者中不患肺癌和患肺癌的频率分别为
吸烟者中不患肺癌和患肺癌的频率分别为
在被调查者中,吸烟者患肺癌的频率是不吸烟者患肺癌的频率的4倍以上,于是,根据频率稳定于概率的原理,我们可以认为吸烟者患肺癌的概率明显大于不吸烟者患肺癌的概率,即吸烟更容易引发肺癌.
例2 甲、乙两机床加工同一种零件,抽检得到它们加工后的零件尺寸x(单位:cm)及个数y,如下表:
零件尺寸x 1.01 1.02 1.03 1.04 1.05
零件 个数y 甲 3 7 8 9 3
乙 7 4 4 4 a
机床加工 零件的质量 合计
合格零件数 不合格零件数
甲
乙
合计
例题讲解
例题讲解
例题讲解
例题讲解
方法技巧
方法技巧
1.打鼾不仅影响别人休息,而且可能与患心脏病有关.下表是一次调查所得的数据:
根据小概率值α=0.001的独立性检验,能否认为每一晚都打鼾与患心脏病有关系?
打鼾 心脏病 合计
患病 未患病
每一晚都打鼾 30 224 254
不打鼾 24 1355 1379
合计 54 1579 1633
巩固练习
巩固练习
1.某省进行高中新课程改革,为了解教师对新课程教学模式的使用情况,某一教育机构对某学校的教师关于新课程教学模式的使用情况进行了问卷调查,共调查了50人,其中有老教师20人,青年教师30人.老教师对新课程教学模式赞同的有10人,不赞同的有10人;青年教师对新课程教学模式赞同的有24人,不赞同的有6人.
(1)根据以上数据建立一个2×2列联表;
(2)试根据小概率值α=0.01的独立性检验,分析对新课程教学模式的赞同情况与教师年龄是否有关系.
巩固练习
解:(1)2×2列联表如表所示:
教师年龄 对新课程教学模式 合计
赞同 不赞同
老教师 10 10 20
青年教师 24 6 30
合计 34 16 50
巩固练习
巩固练习
独立性检验的关注点
(1)步骤:列表,计算,判断;
(2)注意:①χ2计算公式较复杂,一是公式要清楚;二是代入数值时不能张冠李戴;三是计算时要细心;
②判断时把计算结果与临界值比较,其值越大,有关的可信度越高.
方法技巧
方法技巧
3. 学校举行运动会,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下2×2列联表:
运动的喜好 合计
喜爱运动 不喜爱运动
男 10 16
女 6 14
合计 30
巩固练习
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
解:(1)
运动的喜好 合计
喜爱运动 不喜爱运动
男 10 6 16
女 6 8 14
合计 16 14 30
巩固练习
巩固练习
1. 小概率值α的临界值:
忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使得P(χ2 ≥xα)=α成立. 我们称xα为α的临界值,这个临界值就可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
2. χ2计算公式:
3. 基于小概率值α的检验规则是:
当χ2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α;
当χ2
谢 谢 !
