第11章:反比例函数练习题 含解析 2021-2022学年江苏省八年级下学期期末数学试题选编
文档属性
| 名称 | 第11章:反比例函数练习题 含解析 2021-2022学年江苏省八年级下学期期末数学试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 1006.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 07:52:23 | ||
图片预览


文档简介
第11章:反比例函数 练习题
一、单选题
1.(2022春·江苏苏州·八年级统考期末)下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
2.(2022春·江苏淮安·八年级统考期末)矩形的面积为20平方米,它的长y米,宽x米之间的函数表达式是( )
A. B. C. D.
3.(2022春·江苏无锡·八年级统考期末)已知点M (-2,4 ),则下列各点一定与该点在同一反比例函数图像上的是( )
A.(1,8 ) B.(1,-8 ) C.(2,4 ) D.(-4,-2)
4.(2022春·江苏泰州·八年级统考期末)函数的图像可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据所获信息判断,下列直线中与函数的图像没有公共点的是( )
A.经过点且平行于轴的直线
B.经过点且平行于轴的直线
C.经过点且平行于轴的直线
D.经过点且平行于轴的直线
5.(2022春·江苏宿迁·八年级统考期末)在同一直角坐标系中,函数与的图像大致是( )
A.B.C.D.
6.(2022春·江苏连云港·八年级统考期末)如图,直线y=kx(k≠0)与双曲线y=相交于A、C两点,过点A作AB⊥x轴于点B,连接BC,则△ABC的面积为( )
A.8 B.6 C.4 D.2
7.(2022春·江苏淮安·八年级统考期末)已知反比例函数y,下列结论中,不正确的是( )
A.图象必经过点(1,2) B.y的值随x值的增大而减小
C.图象在第一、三象限内 D.若x>1,则0<y<2
8.(2022春·江苏扬州·八年级统考期末)已知反比例函数,下列结论中不正确的是( )
A.其图像经过点 B.其图像分别位于第一、第三象限
C.当时,y随x的增大而增大 D.当时,
9.(2022春·江苏无锡·八年级统考期末)已知点,,都在反比例函数(a是常数)的图象上,且,则,,的大小关系为( )
A. B. C. D.
10.(2022春·江苏连云港·八年级统考期末)两个反比例函数和在第一象限内的图像如图所示,点在的图像上,轴于点,交的图像于点,轴于点,交的图像于点,轴于点,当点在图像上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
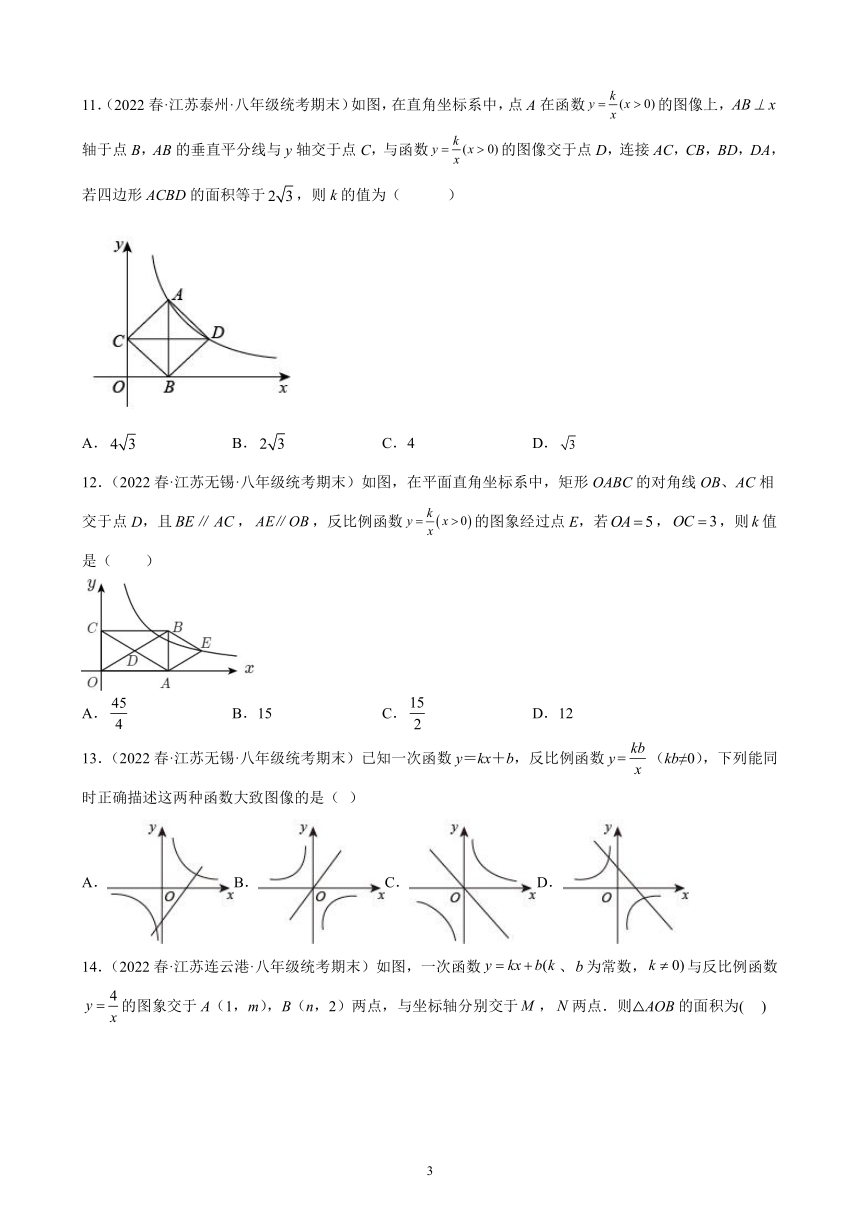
11.(2022春·江苏泰州·八年级统考期末)如图,在直角坐标系中,点A在函数的图像上,轴于点B,AB的垂直平分线与y轴交于点C,与函数的图像交于点D,连接AC,CB,BD,DA,若四边形ACBD的面积等于,则k的值为( )
A. B. C.4 D.
12.(2022春·江苏无锡·八年级统考期末)如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,且,,反比例函数的图象经过点E,若,,则值是( )
A. B.15 C. D.12
13.(2022春·江苏无锡·八年级统考期末)已知一次函数y=kx+b,反比例函数y(kb≠0),下列能同时正确描述这两种函数大致图像的是( )
A.B.C. D.
14.(2022春·江苏连云港·八年级统考期末)如图,一次函数、为常数,与反比例函数的图象交于A(1,m),B(n,2)两点,与坐标轴分别交于,两点.则△AOB的面积为( )
A.3 B.6 C.8 D.12
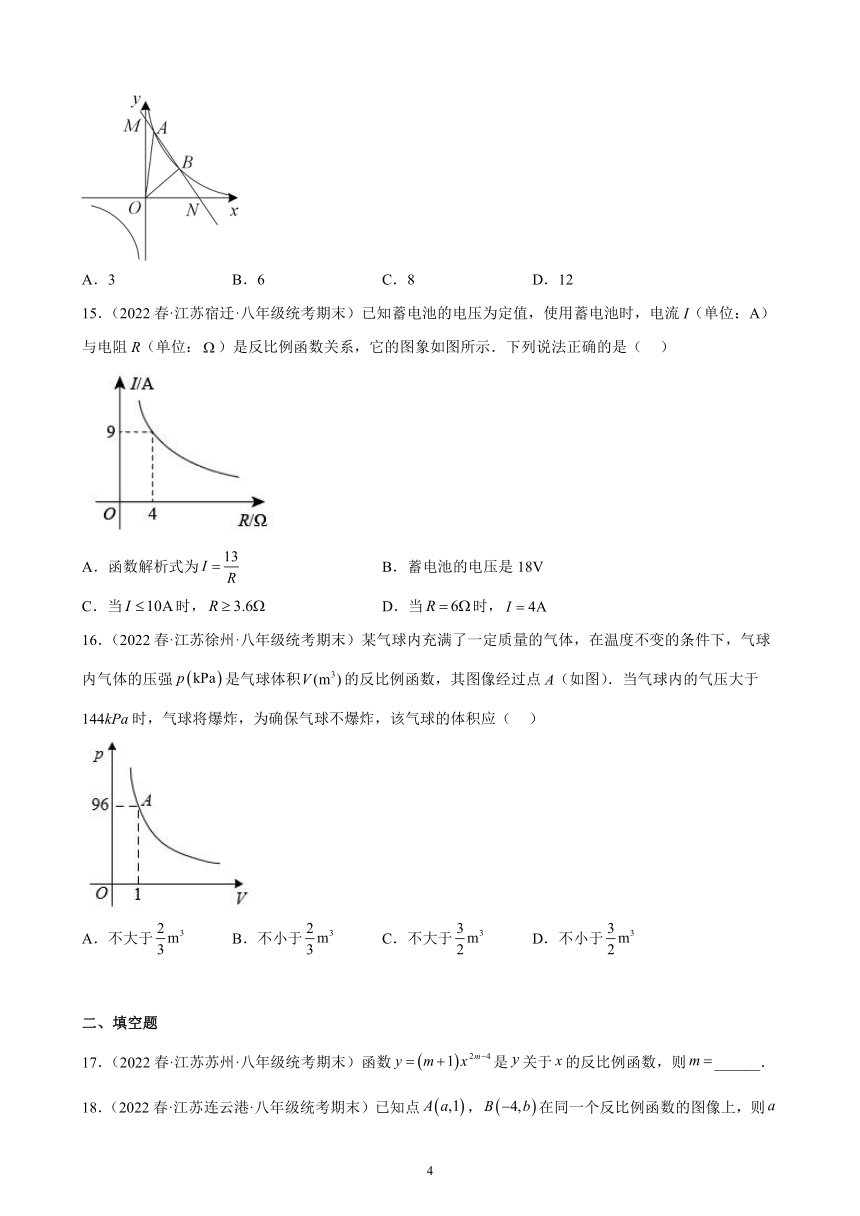
15.(2022春·江苏宿迁·八年级统考期末)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
16.(2022春·江苏徐州·八年级统考期末)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像经过点A(如图).当气球内的气压大于144kPa时,气球将爆炸,为确保气球不爆炸,该气球的体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
二、填空题
17.(2022春·江苏苏州·八年级统考期末)函数是关于的反比例函数,则______.
18.(2022春·江苏连云港·八年级统考期末)已知点,在同一个反比例函数的图像上,则与之间的数量关系是_________.
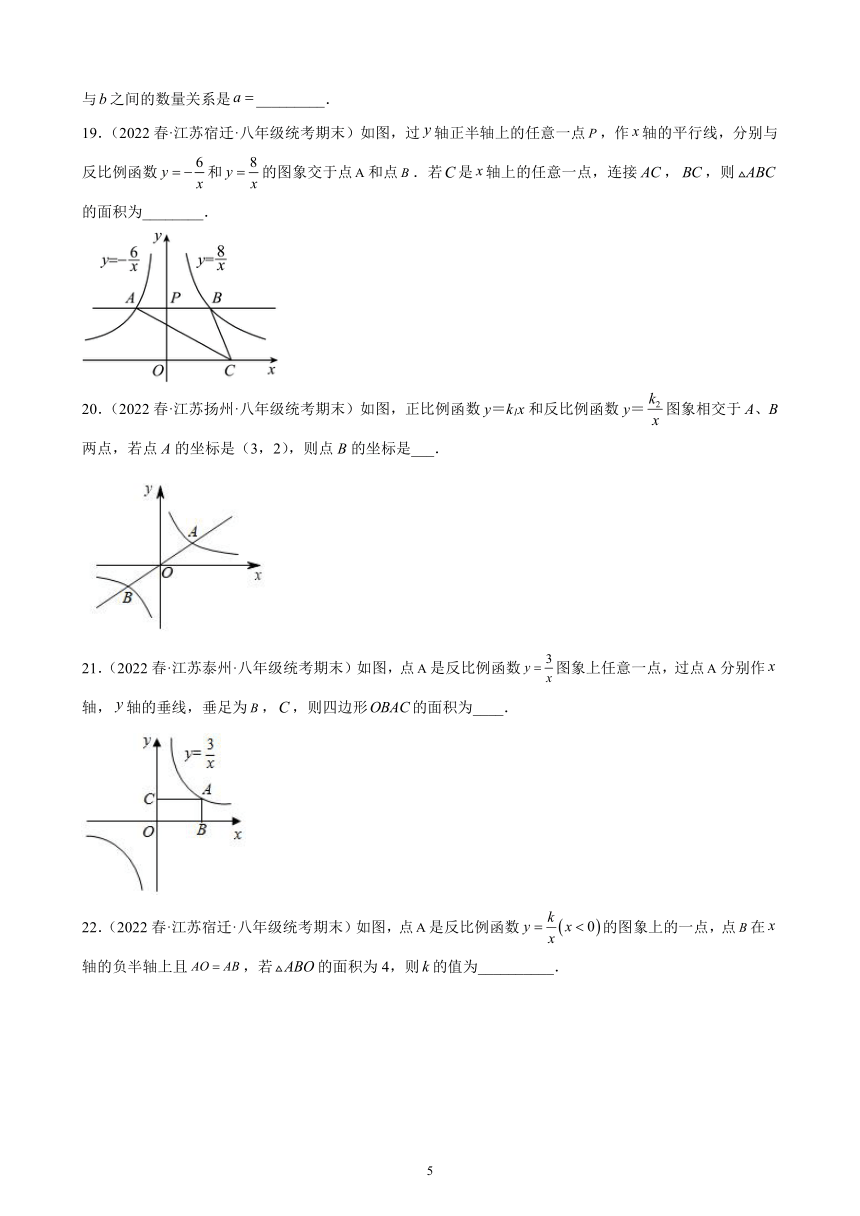
19.(2022春·江苏宿迁·八年级统考期末)如图,过轴正半轴上的任意一点,作轴的平行线,分别与反比例函数和的图象交于点和点.若是轴上的任意一点,连接,,则的面积为________.
20.(2022春·江苏扬州·八年级统考期末)如图,正比例函数y=k1x和反比例函数y=图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是___.
21.(2022春·江苏泰州·八年级统考期末)如图,点是反比例函数图象上任意一点,过点分别作轴,轴的垂线,垂足为,,则四边形的面积为____.
22.(2022春·江苏宿迁·八年级统考期末)如图,点是反比例函数的图象上的一点,点在轴的负半轴上且,若的面积为4,则的值为__________.
23.(2022春·江苏宿迁·八年级统考期末)如图,一辆汽车匀速通过某段公路,所需时间与行驶速度的图像为双曲线的一段,若这段公路行驶速度不得超过,则该汽车通过这段公路最少需要_____h.
24.(2022春·江苏常州·八年级统考期末)如图,点D是矩形OABC的对称中心,E是边AB上一点,反比例函数的图像经过点D、E,且,则k的值是______.
三、解答题
25.(2022春·江苏扬州·八年级统考期末)如图,某养鸡场利用一面长为11m的墙,其他三面用栅栏围成矩形,面积为,设与墙垂直的边长为xm,与墙平行的边长为ym.
(1)直接写出y与x的函数关系式为______;
(2)现有两种方案或,试选择合理的设计方案,并求此栅栏总长.
26.(2022春·江苏泰州·八年级统考期末)如图,直线与双曲线(k为常数,)在第一象限内交于点,且与x轴,y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在坐标轴上,且的面积等于8,求P点的坐标;
(3)将直线AB绕原点旋转180°后与x轴交于点D,与双曲线第三象限内的图像交于点E,猜想四边形ABED的形状,并证明你的猜想.
27.(2022春·江苏淮安·八年级统考期末)如图,菱形OABC的点B在y轴上,点C坐标为(4,3),双曲线的图象经过点A.
(1)菱形OABC的边长为 ;
(2)求双曲线的函数关系式;
(3)①点B关于点O的对称点为D点,过D作直线l垂直于y轴,点P是直线l上一个动点,点E在双曲线上,当P、E、A、B四点构成平行四边形时,求点E的坐标;
②将点P绕点A逆时针旋转90°得点Q,当点Q落在双曲线上时,求点Q的坐标.
28.(2022春·江苏无锡·八年级统考期末)如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=6,OB=3,反比例函数在第一象限的图象经过正方形的顶点C.
(1)求点C的坐标和反比例函数的表达式;
(2)如图2,将正方形ABCD沿x轴向右平移m个单位长度得到正方形,点恰好落在反比例函数的图象上,求此时点的坐标;
(3)在(2)的条件下,点P为x轴上一动点,平面内是否存在点Q,使以点O、、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
29.(2022春·江苏扬州·八年级校联考期末)某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现已知上市30天时,当日销售量为120万件.
(1)写出该商品上市以后销售量y(万件)与时间x(天数)之间的表达式;
(2)求上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数;
(3)广告合同约定,当销售量不低于100万件,并且持续天数不少于12天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”?
30.(2022春·江苏南京·八年级统考期末)如图,在平面直角坐标系中,四边形为正方形,已知点,,点、在第二象限内.
(1)点的坐标_________;
(2)将正方形以每秒1个单位的速度沿轴向右平移秒,若存在某一时刻,使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上,请求出此时的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在轴上的点和反比例函数图象上的点,使得以、、、四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点、的坐标;若不存在,请说明理由.
参考答案:
1.C
【分析】根据反比例函数的定义(一般地,形如(是常数,)的函数叫做是的反比例函数)逐项判断即可得.
【详解】解:A、是正比例函数,则此项不符题意;
B、叫做是的反比例函数,则此项不符题意;
C、叫做是的反比例函数,则此项符合题意;
D、是正比例函数,则此项不符题意;
故选:C.
【点睛】本题考查了反比例函数,熟记定义是解题关键.
2.A
【分析】根据等量关系“长=矩形的面积 宽”,把相关数值代入即可求解.
【详解】解;由题意得:
.
故选:A.
【点睛】本题考查矩形的面积的灵活应用,关键是找到所求量的等量关系.
3.B
【分析】根据点M(-2,4)在反比例函数的图象上,可以求得k的值,从而可以判断各个选项是否正确.
【详解】解:∵点M(-2,4)在反比例函数的图象上,
∴k=xy=-8,
∵1×8=8,故选项A不符合题意,
1×(-8)=-8,故选项B符合题意,
2×4=8,故选项C不符合题意,
-4×(-2)=8,故选项D不符合题意,
故选:B.
【点睛】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.
4.D
【分析】分别计算对应的自变量的值或函数值即可判断.
【详解】解:A、当y=2时,,解得x=,故直线y=2与函数的图像有公共点;
B、当y=-3时, =-3,解得x=0,故直线y=-3与函数的图像有公共点;
C、当x=-1时,,故直线x=-1与函数的图像有公共点;
D、分式有意义的条件是x≠1,∴函数的图像与直线x=1没有公共点;
故选:D.
【点睛】此题考查了求函数值或求自变量的值,分式有意义的条件,正确计算是解题的关键.
5.B
【分析】根据各项中图像的位置判断k的符号是否相同,由此进行判断.
【详解】解:A、中k>0,中k<0,故不符合题意;
B、中k<0,中k<0,故符合题意;
C、中k<0,中k>0,故不符合题意;
D、中k<0且与y轴交于正半轴,中k<0,故不符合题意;
故选:B.
【点睛】此题考查了依据一次函数与反比例函数的图像所经过的象限确定系数的符号,正确掌握各函数的图像与字母系数的关系是解题的关键.
6.C
【分析】利用反比例函数关于原点中心对称,设A点(a,),则C点(-a,),由坐标的特征便可计算△ABC面积;
【详解】解:∵反比例函数图象上任意一点(x,y)关于原点的对称点(-x,-y)也在函数图象上,
∴反比例函数关于原点对称,
设A点(a,),则C点(-a,),
∵AB=,C点到AB的距离为2a,
∴△ABC面积=,
故选: C.
【点睛】本题考查了反比例函数的图象性质,掌握反比例函数关于原点中心对称是解题关键.
7.B
【分析】根据反比例函数图象上点的坐标特点:横纵坐标之积=k,可以判断出A的正误;根据反比例函数的性质:k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小可判断出B、C、D的正误.
【详解】解:A、反比例函数y,所过的点的横纵坐标之积=2,故此选项不符合题意;
B、反比例函数y,在每一象限内y随x的增大而减小,故此选项符合题意;
C、反比例函数y,图象在第一、三象限内,故此选项不合题意;
D、反比例函数y,当x>1时图象在第一象限,y随x的增大而减小,故x>1时0<y<2;
故选:B.
【点睛】此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是熟练掌握反比例函数的性质:(1)反比例函数y(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
8.C
【分析】根据反比例函数的图象与性质逐项分析即可.
【详解】解:将代入解析式,得,故A正确,不符合题意;
由于,则函数图象过一、三象限,在每个象限内,y随x的增大而减小,故B正确,不符合题意、C错误,符合题意;
∵时,,且当时y随x的增大而减小
∴当时,,故D正确,不符合题意,
故选:C.
【点睛】本题考查了反比例函数的图象与性质,反比例函数(k是常数,)的图象是双曲线,当,反比例函数图象的两个分支在第一、三象限,在每一象限内,y随x的增大而减小;当,反比例函数图象的两个分支在第二、四象限,在每一象限内,y随x的增大而增大.
9.D
【分析】根据,判断反比例函数的图象所在位置,结合图象分析函数增减性,利用函数增减性比较自变量的大小.
【详解】解:∵,
∴反比例函数(a是常数)的图象在一、三象限,
如图所示:
当时,,
故选:D.
【点睛】本题考查反比例函数的自变量大小的比较,解题的关键是结合图象,根据反比例函数的增减性分析自变量的大小.
10.C
【分析】①正确,只要证明 即可;
②错误;只有当四边形OCPD为正方形时满足PA= PB;
③正确;由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不
会发生变化;
④正确.只要证明△OBA的面积=矩形OCPD的面积- S ODB- S△BAP - S AOC,四边形ACEB的面积=矩形OCPD的面积- S ODB一S△BAP - S OBE即可.
【详解】①正确;∵A,B在上,
∴S AOC=S BOE
∴OC AC=OE BE,
∴OC AC= OE BE,
∴OC= PD, BE= PC,
∴PD AC= DB PC,
∴
∴AB//CD.故此选项正确.
②错误,不一定,只有当四边形OCPD为正方形时满足PA= PB;
③正确,由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化;故此选项正确.
正确,∵△ODB的面积= OCA的面积=,
∴△ODB与 OCA的面积相等,
同理可得:S ODB= S OBE ,
∵ OBA的面积=矩形OCPD的面积-S ODB- S BAP- S AOC,
四边形ACEB的面积=矩形OCPD的面积- S ODB- S BAP- S OBE .
∴ OBA的面积=四边形ACEB的面积,
故此选项正确,
故一定正确的是①③④
故选:C
【点睛】本题考查反比例函数k是几何意义、矩形的性质、平行线的判定等知识,本题综合性比较强,属于中考填空题中的压轴题.
11.B
【分析】设A(a,),可求出D(2a,),由于对角线垂直,所以面积=对角线乘积的一半即可.
【详解】解:设A(a,),
∵轴于点B,AB的垂直平分线与y轴交于点C,
∴CDx轴,C(0,)
∴点D纵坐标为,
∵点D在函数的图像上,
∴当y=时,x=2a,
∴D(2a,),
∵AB⊥CD,
∴S四边形ACBD=AB CD=×2a×=2,
解得k=2.
故选:B.
【点睛】本题主要考查了反比例函数图像上点的坐标特征以及线段垂直平分线的性质,解题的关键是设出点A和点D的坐标.
12.A
【分析】连接DE,交AB于F,先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,证出四边形AEBD是菱形,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;把点E坐标代入(x>0),求出k的值即可.
【详解】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,OA=5,OC=3,
∴DA=AC,DB=OB,AC=OB,AB=OC=3,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=5,OC=3,
∴EF=DF=OA=,AF=AB=,5+=,
∴点E坐标为:(,).
∵反比例函数y=(x>0)的图象经过点E,
∴k=,
故选:A.
【点睛】本题考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度.
13.D
【分析】根据一次函数的图象确定k和b的符号,进一步确定反比例函数的图象即可.
【详解】解:A选项中根据一次函数图象可知,k>0,b<0,
∴kb<0,
∴反比例函数经过二、四象限,
故A选项不符合题意;
B选项中根据一次函数图象可知,k>0,b>0,
∴kb>0,
∴反比例函数经过一、三象限,
故B选项不符合题意;
C选项中,一次函数b=0,
∵kb≠0,
故C选项不符合题意;
D选项中根据一次函数图象可知,k<0,b>0,
∴kb<0,
∴反比例函数经过二、四象限,
故D选项符合题意;
故选:D.
【点睛】本题考查了反比例函数与一次函数的图象,熟练掌握反比例函数与一次函数的图象与参数的关系是解题的关键.
14.A
【分析】把A(1,m),B(n,2)分别代入y=即可求出m,n,即可得到A、B的坐标,把A,B的坐标代入y=kx+b求得一次函数的解析式,进一步M点的坐标,利用S△BOM-S△AOM求得△AOB的面积.
【详解】解:把A(1,m),B(n,2)分别代入y=,
得m=4,n=2,
∴A(1,4),B(2,2),
将点A(1,4)和B(2,2)代入一次函数y=kx+b,
得,解得.
∴一次函数的表达式y=-2x+6,
令x=0,则y=-2x+6=6,
∴M(0,6),
∴S△AOB=S△BOM-S△AOM=×6×2-×6×1=3,
故选:A.
【点睛】本题主要考查了反比例函数图象上点的坐标图象,待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,三角形面积,熟练掌握待定系数法是解题的关键.
15.C
【分析】将将代入求出U的值,即可判断A,B,D,利用反比例函数的增减性可判断C.
【详解】解:设,将代入可得,故A错误;
∴蓄电池的电压是36V,故B错误;
当时,,该项正确;
当当时,,故D错误,
故选:C.
【点睛】本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.
16.B
【分析】根据题意可知温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,且过点(1,96)故P V=96;故当P≤144,可判断V≥.
【详解】解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=
∵图象过点(1,96)
∴k=96,
即P=
在第一象限内,P随V的增大而减小,
∴当P≤144时,V≥.
故选:B.
【点睛】本题考查了反比例函数的应用,解题的关键是根据图象上的已知点的坐标,利用待定系数法求出函数解析式.
17.
【分析】根据反比例函数的定义可得2m-4=-1且m+1≠0,由此求m的值即可.
【详解】解:∵函数是y关于x的反比例函数,
∴2m-4= 1且m+1≠0,
解得:m=;
故答案为:.
【点睛】本题考查了反比例函数的定义,反比例函数的一般形式是(k≠0),也可以写成(k≠0)或xy=k(k≠0).解题的关键是牢记反比例函数的定义.
18.
【分析】设反比例函数解析式为,根据题意将点代入解析式即可求解.
【详解】解:∵点,在同一个反比例函数的图像上,
设反比例函数解析式为,
∴,
即,
故答案为:.
【点睛】本题考查了反比例函数的性质,掌握反比例函数的性质是解题的关键.
19.7
【分析】根据两平行直线之间共底三角形的面积相等可知,当C点位于O点时,△ABC的面积与△ABO的面积相等,再根据反比例函数的几何意义,即可求解.
【详解】
连接OA、OB,
轴,和同底边AB,
,
,
反比例函数和的图象交于点和点,
,
,
故答案为:7.
【点睛】本题考查了反比例函数的图象和性质,熟练掌握反比例函数上一点向坐标轴作垂线,与原点构成的矩形的面积为这个结论是解题的关键.
20.(﹣3,﹣2)
【分析】由于正比例函数与反比例函数的图象均关于原点对称,所以A、B两点关于原点对称,由关于原点对称的点的坐标特点求出B点坐标即可.
【详解】解:∵正比例函数与反比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∵A的坐标为(3,2),
∴B的坐标为(﹣3,﹣2).
故答案为:(﹣3,﹣2).
【点睛】本题主要考查了关于原点对称点的坐标关系,解题的关键在于能够熟练掌握相关知识进行求解.
21.3
【分析】根据反比例函数的图象上点的坐标性得出|xy|=3,进而得出四边形的面积.
【详解】解:如图所示:可得OB×AB=|xy|=|k|=3,
则四边形的面积为:3,
故答案为:3.
【点睛】本题考查了反比例函数(k≠0)系数k的几何意义:从反比例函数(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
22.
【分析】过点A作AC⊥x轴,设点,可得出xy= k,再根据三角形的面积公式即可得出答案.
【详解】解:过点A作AC⊥x轴于点C,如图所示:
设(),
∵OA= AB,
∴OC = BC,
∴点B (2x,0)
∵点是反比例函数的图象上,
∴,
∵△OAB的面积为4,
∴,
即,
∴,
即,
故答案为:-4.
【点睛】本题考查了反比例函数系数k的几何意义以及等腰三角形的性质,反比例函数图象上的点(x,y)一定满足xy= k.熟练掌握反比例函数的性质是解题的关键.
23.或0.5
【分析】先求出反比例函数解析式为,再求出当v=80时,,根据反比例图象与性质即可求解.
【详解】解:如图,设抛物线解析式为,
∵反比例函数图象经过点(40,1),
∴,
∴反比例函数解析式为,
∴当v=80时,
∴当v≤80时,t≥.
故答案为:或0.5
【点睛】此题主要考查了反比例函数的应用,熟知反比例函数图象与性质,正确求出反比例函数解析式是解题关键.
24.-2
【分析】设点,由题意易得,然后过点D作DH⊥x轴于点H,交OE于点G,进而可得△ODE的面积等于梯形AEDH,最后问题可求解.
【详解】解:设点,
∵点D是矩形OABC的对称中心,
∴,
过点D作DH⊥x轴于点H,交OE于点G,如图所示:
由反比例函数k的几何意义可得:,
∴,
∴,
∴,
∴,
∵,
∴;
故答案为-2.
【点睛】本题主要考查矩形的性质、反比例函数k的几何意义及等积法,熟练掌握矩形的性质、反比例函数k的几何意义及等积法是解题的关键.
25.(1)
(2)22m
【分析】(1))利用矩形的面积计算公式可得出xy= 60,变形后即可得出结论;
(2)利用反比例函数图象上点的坐标特征可求出当x = 5和x = 6时的y值,结合墙长11m即可得出应选x = 6的设计方案,再将其代入2x + y中即可求出此栅栏的总长.
【详解】(1)解:根据题意得:,
∴y与x的函数关系式为:,
故答案为:;
(2)解:当x= 5时,,
∵,
∴不符合题意,舍去;
当x=6时,,
∵,
∴符合题意,此栅栏总长为:
;
答:应选择x = 6的设计方案,此栅栏总长为22m.
【点睛】本题考查了反比例函数的应用,解题的关键是:(1)根据各数量之间的关系,找出y与x的函数关系式;(2)利用反比例函数图象上点的坐标特征,求出x=5和x=6时的y值.
26.(1),
(2),,或
(3)平行四边形,理由见解析
【分析】(1)将点代入直线与双曲线求出k、b的值,即可得出解析式;
(2)利用解析式求出B、C的坐标,分类讨论:当P在x轴、y轴上时,可求出P点的坐标;
(3)根据:对角线互相平分的四边形是平行四边形即可求证.
【详解】(1)解:把代入双曲线(k为常数, ),可得,
∴双曲线的解析式为
把代入直线,可得,
∴直线的解析式为;
(2)在中,令,则;令,则,
,
①当P在x轴上时,设P点的坐标为,
∵的面积等于8
,解得或,
∴P点的坐标为或;
②当P在y轴上时,同理可得P点的坐标为或
综合①②,P点的坐标为,,或.
(3)四边形ABED为平行四边形.
理由如下:,绕原点旋转后对应的的坐标为,,
设旋转后的直线解析式为
解得
∴旋转后的直线解析式为,
由反比例函数的对称性可知:,
即,,
∴四边形ABED为平行四边形.
【点睛】本题考查反比例函数与一次函数的综合、待定系数法求解析式、三角形面积、平行四边形的判断、旋转,涉及数形结合、分类讨论思想,熟练掌握反比例函数和一次函数的图象性质是解题的关键.
27.(1)5
(2)
(3)①当E点坐标为(,15)或(4,-3)或(,-9)时,以P、E、A、B四点构成的四边形是平行四边形;②点Q的坐标为(5,)
【分析】(1)如图所示,连接AC交y轴于J,根据菱形的性质可得AC⊥OB,AJ=JC,OJ=BJ,由点C的坐标为(4,3),得到AJ=JC=4,OJ=BJ=3,则;
(2)先求出A点坐标,然后用待定系数法求出反比例函数解析式即可;
(3)①分AB为以P、E、A、B四点构成平行四边形的边和对角线两种情况讨论求解即可;②过点A作AT⊥PD于T,过点Q作QR⊥AT于R,先求出AT=9,然后证明△APT≌△QRA得到AT=RQ=9,则Q点的横坐标为5,由此求解即可.
【详解】(1)解:如图所示,连接AC交y轴于J,
∵四边形OABC是菱形,
∴AC⊥OB,AJ=JC,OJ=BJ,
∵点C的坐标为(4,3),
∴AJ=JC=4,OJ=BJ=3,
∴,
故答案为:5;
(2)解:∵AJ=JC=4,OJ=BJ=3,
∴点A的坐标为(-4,3),
∵反比例函数经过点A(-4,3),
∴,
∴,
∴反比例函数解析式为;
(3)解:①设E点坐标为(m,),
∵OJ=BJ=3,
∴OB=6,
∴B点坐标为(0,6),
∴D点坐标为(0,-6),
∴直线l为,
设P点坐标为(a,-6)
当AB是以P、E、A、B四点构成平行四边形的对角线时,
∵线段AB与线段PE的中点坐标相同,
∴,
∴,
∴点E的坐标为(,15);
如图所示,当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,
∵与的中点坐标相同,
∴,
∴,
∴的坐标为(4,-3);
同理可以求出当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,点的坐标为(,-9);
综上所述,当E点坐标为(,15)或(4,-3)或(,-9)时,以P、E、A、B四点构成的四边形是平行四边形;
②如图所示,过点A作AT⊥PD于T,过点Q作QR⊥AT于R,
∵点A的坐标为(-4,3),直线l为,
∴AT=9,
∵∠ATP=∠QRA=∠PAQ=90°,
∴∠PAT+∠APT=90°,∠PAT+∠QAR=90°,
∴∠APT=∠QAR,
又∵AP=QA,
∴△APT≌△QRA(AAS),
∴AT=RQ=9,
∴Q点的横坐标为5,
∵Q在反比例函数上,
∴,
∴点Q的坐标为(5,).
【点睛】本题主要考查了反比例函数与几何综合,菱形的性质,勾股定理,全等三角形的性质与判定,平行四边形的性质,坐标与图形,熟知相关知识是解题的关键.
28.(1)C(9,3),
(2)
(3)存在,(-3,6)或(12,6)或或
【分析】(1)过点C作CH⊥x轴,交于点H,根据正方形的性质及各角之间的关系得出∠OAB=∠CBH,利用全等三角形的判定和性质得出BH=OA=6,CH=OB=3,即可确定点的坐标;
(2)利用(1)中方法确定D(6,9),由点A’恰好落在反比例函数图象上,确定函数图象的平移方式即可得出点D’的坐标;
(3)根据题意进行分类讨论:当OA’=OP时;当A’O=A’P时;当PO=PA’时;分别利用菱形的性质及等腰三角形的性质求解即可.
【详解】(1)解:过点C作CH⊥x轴,交于点H,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBH=90°,
∵∠ABO+∠OAB=90°,
∴∠OAB=∠CBH,
∴ AOB BHC,
∴BH=OA=6,CH=OB=3,
∴OH=9,
∴C(9,3)
∵反比例函数在第一象限的图象经过正方形的顶点C,
∴k=9×3=27,
∴;
(2)如图所示,过点D作轴,,,
同(1)方法可得:,
∵,
∴四边形OGEA为矩形,
∴AO=EG=6,DE=OB=3,AE=AO=6,
∴D(6,9),
∵点A’恰好落在反比例函数图象上,
∴当y=6时,x=,
∴m=,
∴D’(6+,9)即D’(,9);
(3)当OA’=OP时,如图所示:
∵A’(,6),
OA’=,
四边形OPQA’是菱形,
A’Q∥OP,A’Q=OP,
Q(12,6),
当点Q’在第二象限时,Q’(-3,6);
当A’O=A’P时,如图所示:
点A’与点Q关于x轴对称,
Q(,-6);
当PO=PA’时,如图设P(m,0),
则PO=PA’,
∴,
解得:,
∴OP=A’Q=,
∴Q(,6),
综上可得:Q(,6)或(,-6)或(12,6)或(-3,6) .
【点睛】题目主要考查反比例函数的性质,正方形的性质,平移的性质,全等三角形的判定和性质,菱形的性质,等腰三角形的性质等,理解题意,(3)中根据等腰三角形进行分类讨论是解题关键.
29.(1);
(2)8
(3)能
【分析】(1)分类讨论当时或当时,分别设函数解析式,代入求值即可;
(2)分类讨论当时或当时,分别不等式即可求解;
(3)分类讨论当时或当时,分别不等式即可求解;
【详解】(1)解:根据题意可知:
当时,设与的函数解析式为,
∴,
解得:,
∴;
当时,设与的函数解析式为,
∴,
解得:
∴
综上所述,该商品上市以后销售量y(万件)与时间x(天数)之间的表达式为:;.
(2)解:当时,
令,
解得:,
∴,
∴销量不到36万件的天数为8天;
当时,
令,
解得: (不符合题意),
∴上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数为8天;
(3)解:当时,
令,
解得:
∴,
∴销量超过100万件的天数为6天,
当时,
令,
解得:
∴,
销量超过100万件的天数为6天,
综上所述,销售量不低于100万件,并且持续天数为12天,广告设计师可以拿到“特殊贡献奖”.
【点睛】本题考查了分段函数的实际运用,把握正比函数、反比例函数的图像及性质和运用分类讨论思想是解决本题的关键.
30.(1)
(2),
(3)存在,点、的坐标为、或、或P(-7,0)、Q(-3,-2).
【分析】(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,由正方形的性质结合同角的余角相等即可证出△ADE≌△BAF,从而得出DE=AF,AE=BF,再结合点A、D的坐标即可求出点B的坐标;
(2)设反比例函数为,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
【详解】(1)解:(1)过点作轴于点,过点作轴于点,如图1所示.
∵四边形为正方形,
∴,,
∵,,
∴.
在和中,
,
∴,
∴,.
∵点,,
∴,,
∴点的坐标为,即.
故答案为:.
(2)设反比例函数为,
由题意得:点坐标为,点坐标为,
∵点和在该比例函数图象上,
∴,
解得:,,
∴反比例函数解析式为.
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,).
以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:
①B′D′为对角线时,
∵四边形B′PD′Q为平行四边形,
∴,
解得:,
∴P(,0),Q(,4);
②当B′D′为边时.
∵四边形PQB′D′为平行四边形,
∴,
解得:,
∴P(7,0),Q(3,2);
∵四边形B′QPD′为平行四边形,
∴,
解得:.
∴P(-7,0)、Q(-3,-2).
综上可知:存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形,
符合题意的点P、Q的坐标为:P(,0)、Q(,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).
【点睛】本题考查了反比例函数图象上点的坐标特征、正方形的性质、全等三角形的判定及性质、平行四边形的性质以及解方程组,解题的关键是:(1)证出△ADE≌△BAF;(2)找出关于k、t的二元一次方程组;(3)分类讨论.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,利用反比例函数图形上点的坐标表示出来反比例函数系数k是关键.
一、单选题
1.(2022春·江苏苏州·八年级统考期末)下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
2.(2022春·江苏淮安·八年级统考期末)矩形的面积为20平方米,它的长y米,宽x米之间的函数表达式是( )
A. B. C. D.
3.(2022春·江苏无锡·八年级统考期末)已知点M (-2,4 ),则下列各点一定与该点在同一反比例函数图像上的是( )
A.(1,8 ) B.(1,-8 ) C.(2,4 ) D.(-4,-2)
4.(2022春·江苏泰州·八年级统考期末)函数的图像可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据所获信息判断,下列直线中与函数的图像没有公共点的是( )
A.经过点且平行于轴的直线
B.经过点且平行于轴的直线
C.经过点且平行于轴的直线
D.经过点且平行于轴的直线
5.(2022春·江苏宿迁·八年级统考期末)在同一直角坐标系中,函数与的图像大致是( )
A.B.C.D.
6.(2022春·江苏连云港·八年级统考期末)如图,直线y=kx(k≠0)与双曲线y=相交于A、C两点,过点A作AB⊥x轴于点B,连接BC,则△ABC的面积为( )
A.8 B.6 C.4 D.2
7.(2022春·江苏淮安·八年级统考期末)已知反比例函数y,下列结论中,不正确的是( )
A.图象必经过点(1,2) B.y的值随x值的增大而减小
C.图象在第一、三象限内 D.若x>1,则0<y<2
8.(2022春·江苏扬州·八年级统考期末)已知反比例函数,下列结论中不正确的是( )
A.其图像经过点 B.其图像分别位于第一、第三象限
C.当时,y随x的增大而增大 D.当时,
9.(2022春·江苏无锡·八年级统考期末)已知点,,都在反比例函数(a是常数)的图象上,且,则,,的大小关系为( )
A. B. C. D.
10.(2022春·江苏连云港·八年级统考期末)两个反比例函数和在第一象限内的图像如图所示,点在的图像上,轴于点,交的图像于点,轴于点,交的图像于点,轴于点,当点在图像上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
11.(2022春·江苏泰州·八年级统考期末)如图,在直角坐标系中,点A在函数的图像上,轴于点B,AB的垂直平分线与y轴交于点C,与函数的图像交于点D,连接AC,CB,BD,DA,若四边形ACBD的面积等于,则k的值为( )
A. B. C.4 D.
12.(2022春·江苏无锡·八年级统考期末)如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,且,,反比例函数的图象经过点E,若,,则值是( )
A. B.15 C. D.12
13.(2022春·江苏无锡·八年级统考期末)已知一次函数y=kx+b,反比例函数y(kb≠0),下列能同时正确描述这两种函数大致图像的是( )
A.B.C. D.
14.(2022春·江苏连云港·八年级统考期末)如图,一次函数、为常数,与反比例函数的图象交于A(1,m),B(n,2)两点,与坐标轴分别交于,两点.则△AOB的面积为( )
A.3 B.6 C.8 D.12
15.(2022春·江苏宿迁·八年级统考期末)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
16.(2022春·江苏徐州·八年级统考期末)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像经过点A(如图).当气球内的气压大于144kPa时,气球将爆炸,为确保气球不爆炸,该气球的体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
二、填空题
17.(2022春·江苏苏州·八年级统考期末)函数是关于的反比例函数,则______.
18.(2022春·江苏连云港·八年级统考期末)已知点,在同一个反比例函数的图像上,则与之间的数量关系是_________.
19.(2022春·江苏宿迁·八年级统考期末)如图,过轴正半轴上的任意一点,作轴的平行线,分别与反比例函数和的图象交于点和点.若是轴上的任意一点,连接,,则的面积为________.
20.(2022春·江苏扬州·八年级统考期末)如图,正比例函数y=k1x和反比例函数y=图象相交于A、B两点,若点A的坐标是(3,2),则点B的坐标是___.
21.(2022春·江苏泰州·八年级统考期末)如图,点是反比例函数图象上任意一点,过点分别作轴,轴的垂线,垂足为,,则四边形的面积为____.
22.(2022春·江苏宿迁·八年级统考期末)如图,点是反比例函数的图象上的一点,点在轴的负半轴上且,若的面积为4,则的值为__________.
23.(2022春·江苏宿迁·八年级统考期末)如图,一辆汽车匀速通过某段公路,所需时间与行驶速度的图像为双曲线的一段,若这段公路行驶速度不得超过,则该汽车通过这段公路最少需要_____h.
24.(2022春·江苏常州·八年级统考期末)如图,点D是矩形OABC的对称中心,E是边AB上一点,反比例函数的图像经过点D、E,且,则k的值是______.
三、解答题
25.(2022春·江苏扬州·八年级统考期末)如图,某养鸡场利用一面长为11m的墙,其他三面用栅栏围成矩形,面积为,设与墙垂直的边长为xm,与墙平行的边长为ym.
(1)直接写出y与x的函数关系式为______;
(2)现有两种方案或,试选择合理的设计方案,并求此栅栏总长.
26.(2022春·江苏泰州·八年级统考期末)如图,直线与双曲线(k为常数,)在第一象限内交于点,且与x轴,y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在坐标轴上,且的面积等于8,求P点的坐标;
(3)将直线AB绕原点旋转180°后与x轴交于点D,与双曲线第三象限内的图像交于点E,猜想四边形ABED的形状,并证明你的猜想.
27.(2022春·江苏淮安·八年级统考期末)如图,菱形OABC的点B在y轴上,点C坐标为(4,3),双曲线的图象经过点A.
(1)菱形OABC的边长为 ;
(2)求双曲线的函数关系式;
(3)①点B关于点O的对称点为D点,过D作直线l垂直于y轴,点P是直线l上一个动点,点E在双曲线上,当P、E、A、B四点构成平行四边形时,求点E的坐标;
②将点P绕点A逆时针旋转90°得点Q,当点Q落在双曲线上时,求点Q的坐标.
28.(2022春·江苏无锡·八年级统考期末)如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=6,OB=3,反比例函数在第一象限的图象经过正方形的顶点C.
(1)求点C的坐标和反比例函数的表达式;
(2)如图2,将正方形ABCD沿x轴向右平移m个单位长度得到正方形,点恰好落在反比例函数的图象上,求此时点的坐标;
(3)在(2)的条件下,点P为x轴上一动点,平面内是否存在点Q,使以点O、、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
29.(2022春·江苏扬州·八年级校联考期末)某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现已知上市30天时,当日销售量为120万件.
(1)写出该商品上市以后销售量y(万件)与时间x(天数)之间的表达式;
(2)求上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数;
(3)广告合同约定,当销售量不低于100万件,并且持续天数不少于12天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”?
30.(2022春·江苏南京·八年级统考期末)如图,在平面直角坐标系中,四边形为正方形,已知点,,点、在第二象限内.
(1)点的坐标_________;
(2)将正方形以每秒1个单位的速度沿轴向右平移秒,若存在某一时刻,使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上,请求出此时的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在轴上的点和反比例函数图象上的点,使得以、、、四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点、的坐标;若不存在,请说明理由.
参考答案:
1.C
【分析】根据反比例函数的定义(一般地,形如(是常数,)的函数叫做是的反比例函数)逐项判断即可得.
【详解】解:A、是正比例函数,则此项不符题意;
B、叫做是的反比例函数,则此项不符题意;
C、叫做是的反比例函数,则此项符合题意;
D、是正比例函数,则此项不符题意;
故选:C.
【点睛】本题考查了反比例函数,熟记定义是解题关键.
2.A
【分析】根据等量关系“长=矩形的面积 宽”,把相关数值代入即可求解.
【详解】解;由题意得:
.
故选:A.
【点睛】本题考查矩形的面积的灵活应用,关键是找到所求量的等量关系.
3.B
【分析】根据点M(-2,4)在反比例函数的图象上,可以求得k的值,从而可以判断各个选项是否正确.
【详解】解:∵点M(-2,4)在反比例函数的图象上,
∴k=xy=-8,
∵1×8=8,故选项A不符合题意,
1×(-8)=-8,故选项B符合题意,
2×4=8,故选项C不符合题意,
-4×(-2)=8,故选项D不符合题意,
故选:B.
【点睛】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.
4.D
【分析】分别计算对应的自变量的值或函数值即可判断.
【详解】解:A、当y=2时,,解得x=,故直线y=2与函数的图像有公共点;
B、当y=-3时, =-3,解得x=0,故直线y=-3与函数的图像有公共点;
C、当x=-1时,,故直线x=-1与函数的图像有公共点;
D、分式有意义的条件是x≠1,∴函数的图像与直线x=1没有公共点;
故选:D.
【点睛】此题考查了求函数值或求自变量的值,分式有意义的条件,正确计算是解题的关键.
5.B
【分析】根据各项中图像的位置判断k的符号是否相同,由此进行判断.
【详解】解:A、中k>0,中k<0,故不符合题意;
B、中k<0,中k<0,故符合题意;
C、中k<0,中k>0,故不符合题意;
D、中k<0且与y轴交于正半轴,中k<0,故不符合题意;
故选:B.
【点睛】此题考查了依据一次函数与反比例函数的图像所经过的象限确定系数的符号,正确掌握各函数的图像与字母系数的关系是解题的关键.
6.C
【分析】利用反比例函数关于原点中心对称,设A点(a,),则C点(-a,),由坐标的特征便可计算△ABC面积;
【详解】解:∵反比例函数图象上任意一点(x,y)关于原点的对称点(-x,-y)也在函数图象上,
∴反比例函数关于原点对称,
设A点(a,),则C点(-a,),
∵AB=,C点到AB的距离为2a,
∴△ABC面积=,
故选: C.
【点睛】本题考查了反比例函数的图象性质,掌握反比例函数关于原点中心对称是解题关键.
7.B
【分析】根据反比例函数图象上点的坐标特点:横纵坐标之积=k,可以判断出A的正误;根据反比例函数的性质:k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小可判断出B、C、D的正误.
【详解】解:A、反比例函数y,所过的点的横纵坐标之积=2,故此选项不符合题意;
B、反比例函数y,在每一象限内y随x的增大而减小,故此选项符合题意;
C、反比例函数y,图象在第一、三象限内,故此选项不合题意;
D、反比例函数y,当x>1时图象在第一象限,y随x的增大而减小,故x>1时0<y<2;
故选:B.
【点睛】此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是熟练掌握反比例函数的性质:(1)反比例函数y(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
8.C
【分析】根据反比例函数的图象与性质逐项分析即可.
【详解】解:将代入解析式,得,故A正确,不符合题意;
由于,则函数图象过一、三象限,在每个象限内,y随x的增大而减小,故B正确,不符合题意、C错误,符合题意;
∵时,,且当时y随x的增大而减小
∴当时,,故D正确,不符合题意,
故选:C.
【点睛】本题考查了反比例函数的图象与性质,反比例函数(k是常数,)的图象是双曲线,当,反比例函数图象的两个分支在第一、三象限,在每一象限内,y随x的增大而减小;当,反比例函数图象的两个分支在第二、四象限,在每一象限内,y随x的增大而增大.
9.D
【分析】根据,判断反比例函数的图象所在位置,结合图象分析函数增减性,利用函数增减性比较自变量的大小.
【详解】解:∵,
∴反比例函数(a是常数)的图象在一、三象限,
如图所示:
当时,,
故选:D.
【点睛】本题考查反比例函数的自变量大小的比较,解题的关键是结合图象,根据反比例函数的增减性分析自变量的大小.
10.C
【分析】①正确,只要证明 即可;
②错误;只有当四边形OCPD为正方形时满足PA= PB;
③正确;由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不
会发生变化;
④正确.只要证明△OBA的面积=矩形OCPD的面积- S ODB- S△BAP - S AOC,四边形ACEB的面积=矩形OCPD的面积- S ODB一S△BAP - S OBE即可.
【详解】①正确;∵A,B在上,
∴S AOC=S BOE
∴OC AC=OE BE,
∴OC AC= OE BE,
∴OC= PD, BE= PC,
∴PD AC= DB PC,
∴
∴AB//CD.故此选项正确.
②错误,不一定,只有当四边形OCPD为正方形时满足PA= PB;
③正确,由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化;故此选项正确.
正确,∵△ODB的面积= OCA的面积=,
∴△ODB与 OCA的面积相等,
同理可得:S ODB= S OBE ,
∵ OBA的面积=矩形OCPD的面积-S ODB- S BAP- S AOC,
四边形ACEB的面积=矩形OCPD的面积- S ODB- S BAP- S OBE .
∴ OBA的面积=四边形ACEB的面积,
故此选项正确,
故一定正确的是①③④
故选:C
【点睛】本题考查反比例函数k是几何意义、矩形的性质、平行线的判定等知识,本题综合性比较强,属于中考填空题中的压轴题.
11.B
【分析】设A(a,),可求出D(2a,),由于对角线垂直,所以面积=对角线乘积的一半即可.
【详解】解:设A(a,),
∵轴于点B,AB的垂直平分线与y轴交于点C,
∴CDx轴,C(0,)
∴点D纵坐标为,
∵点D在函数的图像上,
∴当y=时,x=2a,
∴D(2a,),
∵AB⊥CD,
∴S四边形ACBD=AB CD=×2a×=2,
解得k=2.
故选:B.
【点睛】本题主要考查了反比例函数图像上点的坐标特征以及线段垂直平分线的性质,解题的关键是设出点A和点D的坐标.
12.A
【分析】连接DE,交AB于F,先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,证出四边形AEBD是菱形,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;把点E坐标代入(x>0),求出k的值即可.
【详解】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,OA=5,OC=3,
∴DA=AC,DB=OB,AC=OB,AB=OC=3,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=5,OC=3,
∴EF=DF=OA=,AF=AB=,5+=,
∴点E坐标为:(,).
∵反比例函数y=(x>0)的图象经过点E,
∴k=,
故选:A.
【点睛】本题考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度.
13.D
【分析】根据一次函数的图象确定k和b的符号,进一步确定反比例函数的图象即可.
【详解】解:A选项中根据一次函数图象可知,k>0,b<0,
∴kb<0,
∴反比例函数经过二、四象限,
故A选项不符合题意;
B选项中根据一次函数图象可知,k>0,b>0,
∴kb>0,
∴反比例函数经过一、三象限,
故B选项不符合题意;
C选项中,一次函数b=0,
∵kb≠0,
故C选项不符合题意;
D选项中根据一次函数图象可知,k<0,b>0,
∴kb<0,
∴反比例函数经过二、四象限,
故D选项符合题意;
故选:D.
【点睛】本题考查了反比例函数与一次函数的图象,熟练掌握反比例函数与一次函数的图象与参数的关系是解题的关键.
14.A
【分析】把A(1,m),B(n,2)分别代入y=即可求出m,n,即可得到A、B的坐标,把A,B的坐标代入y=kx+b求得一次函数的解析式,进一步M点的坐标,利用S△BOM-S△AOM求得△AOB的面积.
【详解】解:把A(1,m),B(n,2)分别代入y=,
得m=4,n=2,
∴A(1,4),B(2,2),
将点A(1,4)和B(2,2)代入一次函数y=kx+b,
得,解得.
∴一次函数的表达式y=-2x+6,
令x=0,则y=-2x+6=6,
∴M(0,6),
∴S△AOB=S△BOM-S△AOM=×6×2-×6×1=3,
故选:A.
【点睛】本题主要考查了反比例函数图象上点的坐标图象,待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,三角形面积,熟练掌握待定系数法是解题的关键.
15.C
【分析】将将代入求出U的值,即可判断A,B,D,利用反比例函数的增减性可判断C.
【详解】解:设,将代入可得,故A错误;
∴蓄电池的电压是36V,故B错误;
当时,,该项正确;
当当时,,故D错误,
故选:C.
【点睛】本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.
16.B
【分析】根据题意可知温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,且过点(1,96)故P V=96;故当P≤144,可判断V≥.
【详解】解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=
∵图象过点(1,96)
∴k=96,
即P=
在第一象限内,P随V的增大而减小,
∴当P≤144时,V≥.
故选:B.
【点睛】本题考查了反比例函数的应用,解题的关键是根据图象上的已知点的坐标,利用待定系数法求出函数解析式.
17.
【分析】根据反比例函数的定义可得2m-4=-1且m+1≠0,由此求m的值即可.
【详解】解:∵函数是y关于x的反比例函数,
∴2m-4= 1且m+1≠0,
解得:m=;
故答案为:.
【点睛】本题考查了反比例函数的定义,反比例函数的一般形式是(k≠0),也可以写成(k≠0)或xy=k(k≠0).解题的关键是牢记反比例函数的定义.
18.
【分析】设反比例函数解析式为,根据题意将点代入解析式即可求解.
【详解】解:∵点,在同一个反比例函数的图像上,
设反比例函数解析式为,
∴,
即,
故答案为:.
【点睛】本题考查了反比例函数的性质,掌握反比例函数的性质是解题的关键.
19.7
【分析】根据两平行直线之间共底三角形的面积相等可知,当C点位于O点时,△ABC的面积与△ABO的面积相等,再根据反比例函数的几何意义,即可求解.
【详解】
连接OA、OB,
轴,和同底边AB,
,
,
反比例函数和的图象交于点和点,
,
,
故答案为:7.
【点睛】本题考查了反比例函数的图象和性质,熟练掌握反比例函数上一点向坐标轴作垂线,与原点构成的矩形的面积为这个结论是解题的关键.
20.(﹣3,﹣2)
【分析】由于正比例函数与反比例函数的图象均关于原点对称,所以A、B两点关于原点对称,由关于原点对称的点的坐标特点求出B点坐标即可.
【详解】解:∵正比例函数与反比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∵A的坐标为(3,2),
∴B的坐标为(﹣3,﹣2).
故答案为:(﹣3,﹣2).
【点睛】本题主要考查了关于原点对称点的坐标关系,解题的关键在于能够熟练掌握相关知识进行求解.
21.3
【分析】根据反比例函数的图象上点的坐标性得出|xy|=3,进而得出四边形的面积.
【详解】解:如图所示:可得OB×AB=|xy|=|k|=3,
则四边形的面积为:3,
故答案为:3.
【点睛】本题考查了反比例函数(k≠0)系数k的几何意义:从反比例函数(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
22.
【分析】过点A作AC⊥x轴,设点,可得出xy= k,再根据三角形的面积公式即可得出答案.
【详解】解:过点A作AC⊥x轴于点C,如图所示:
设(),
∵OA= AB,
∴OC = BC,
∴点B (2x,0)
∵点是反比例函数的图象上,
∴,
∵△OAB的面积为4,
∴,
即,
∴,
即,
故答案为:-4.
【点睛】本题考查了反比例函数系数k的几何意义以及等腰三角形的性质,反比例函数图象上的点(x,y)一定满足xy= k.熟练掌握反比例函数的性质是解题的关键.
23.或0.5
【分析】先求出反比例函数解析式为,再求出当v=80时,,根据反比例图象与性质即可求解.
【详解】解:如图,设抛物线解析式为,
∵反比例函数图象经过点(40,1),
∴,
∴反比例函数解析式为,
∴当v=80时,
∴当v≤80时,t≥.
故答案为:或0.5
【点睛】此题主要考查了反比例函数的应用,熟知反比例函数图象与性质,正确求出反比例函数解析式是解题关键.
24.-2
【分析】设点,由题意易得,然后过点D作DH⊥x轴于点H,交OE于点G,进而可得△ODE的面积等于梯形AEDH,最后问题可求解.
【详解】解:设点,
∵点D是矩形OABC的对称中心,
∴,
过点D作DH⊥x轴于点H,交OE于点G,如图所示:
由反比例函数k的几何意义可得:,
∴,
∴,
∴,
∴,
∵,
∴;
故答案为-2.
【点睛】本题主要考查矩形的性质、反比例函数k的几何意义及等积法,熟练掌握矩形的性质、反比例函数k的几何意义及等积法是解题的关键.
25.(1)
(2)22m
【分析】(1))利用矩形的面积计算公式可得出xy= 60,变形后即可得出结论;
(2)利用反比例函数图象上点的坐标特征可求出当x = 5和x = 6时的y值,结合墙长11m即可得出应选x = 6的设计方案,再将其代入2x + y中即可求出此栅栏的总长.
【详解】(1)解:根据题意得:,
∴y与x的函数关系式为:,
故答案为:;
(2)解:当x= 5时,,
∵,
∴不符合题意,舍去;
当x=6时,,
∵,
∴符合题意,此栅栏总长为:
;
答:应选择x = 6的设计方案,此栅栏总长为22m.
【点睛】本题考查了反比例函数的应用,解题的关键是:(1)根据各数量之间的关系,找出y与x的函数关系式;(2)利用反比例函数图象上点的坐标特征,求出x=5和x=6时的y值.
26.(1),
(2),,或
(3)平行四边形,理由见解析
【分析】(1)将点代入直线与双曲线求出k、b的值,即可得出解析式;
(2)利用解析式求出B、C的坐标,分类讨论:当P在x轴、y轴上时,可求出P点的坐标;
(3)根据:对角线互相平分的四边形是平行四边形即可求证.
【详解】(1)解:把代入双曲线(k为常数, ),可得,
∴双曲线的解析式为
把代入直线,可得,
∴直线的解析式为;
(2)在中,令,则;令,则,
,
①当P在x轴上时,设P点的坐标为,
∵的面积等于8
,解得或,
∴P点的坐标为或;
②当P在y轴上时,同理可得P点的坐标为或
综合①②,P点的坐标为,,或.
(3)四边形ABED为平行四边形.
理由如下:,绕原点旋转后对应的的坐标为,,
设旋转后的直线解析式为
解得
∴旋转后的直线解析式为,
由反比例函数的对称性可知:,
即,,
∴四边形ABED为平行四边形.
【点睛】本题考查反比例函数与一次函数的综合、待定系数法求解析式、三角形面积、平行四边形的判断、旋转,涉及数形结合、分类讨论思想,熟练掌握反比例函数和一次函数的图象性质是解题的关键.
27.(1)5
(2)
(3)①当E点坐标为(,15)或(4,-3)或(,-9)时,以P、E、A、B四点构成的四边形是平行四边形;②点Q的坐标为(5,)
【分析】(1)如图所示,连接AC交y轴于J,根据菱形的性质可得AC⊥OB,AJ=JC,OJ=BJ,由点C的坐标为(4,3),得到AJ=JC=4,OJ=BJ=3,则;
(2)先求出A点坐标,然后用待定系数法求出反比例函数解析式即可;
(3)①分AB为以P、E、A、B四点构成平行四边形的边和对角线两种情况讨论求解即可;②过点A作AT⊥PD于T,过点Q作QR⊥AT于R,先求出AT=9,然后证明△APT≌△QRA得到AT=RQ=9,则Q点的横坐标为5,由此求解即可.
【详解】(1)解:如图所示,连接AC交y轴于J,
∵四边形OABC是菱形,
∴AC⊥OB,AJ=JC,OJ=BJ,
∵点C的坐标为(4,3),
∴AJ=JC=4,OJ=BJ=3,
∴,
故答案为:5;
(2)解:∵AJ=JC=4,OJ=BJ=3,
∴点A的坐标为(-4,3),
∵反比例函数经过点A(-4,3),
∴,
∴,
∴反比例函数解析式为;
(3)解:①设E点坐标为(m,),
∵OJ=BJ=3,
∴OB=6,
∴B点坐标为(0,6),
∴D点坐标为(0,-6),
∴直线l为,
设P点坐标为(a,-6)
当AB是以P、E、A、B四点构成平行四边形的对角线时,
∵线段AB与线段PE的中点坐标相同,
∴,
∴,
∴点E的坐标为(,15);
如图所示,当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,
∵与的中点坐标相同,
∴,
∴,
∴的坐标为(4,-3);
同理可以求出当AB为平行四边形的边时,即以P、E、A、B四点构成平行四边形为时,点的坐标为(,-9);
综上所述,当E点坐标为(,15)或(4,-3)或(,-9)时,以P、E、A、B四点构成的四边形是平行四边形;
②如图所示,过点A作AT⊥PD于T,过点Q作QR⊥AT于R,
∵点A的坐标为(-4,3),直线l为,
∴AT=9,
∵∠ATP=∠QRA=∠PAQ=90°,
∴∠PAT+∠APT=90°,∠PAT+∠QAR=90°,
∴∠APT=∠QAR,
又∵AP=QA,
∴△APT≌△QRA(AAS),
∴AT=RQ=9,
∴Q点的横坐标为5,
∵Q在反比例函数上,
∴,
∴点Q的坐标为(5,).
【点睛】本题主要考查了反比例函数与几何综合,菱形的性质,勾股定理,全等三角形的性质与判定,平行四边形的性质,坐标与图形,熟知相关知识是解题的关键.
28.(1)C(9,3),
(2)
(3)存在,(-3,6)或(12,6)或或
【分析】(1)过点C作CH⊥x轴,交于点H,根据正方形的性质及各角之间的关系得出∠OAB=∠CBH,利用全等三角形的判定和性质得出BH=OA=6,CH=OB=3,即可确定点的坐标;
(2)利用(1)中方法确定D(6,9),由点A’恰好落在反比例函数图象上,确定函数图象的平移方式即可得出点D’的坐标;
(3)根据题意进行分类讨论:当OA’=OP时;当A’O=A’P时;当PO=PA’时;分别利用菱形的性质及等腰三角形的性质求解即可.
【详解】(1)解:过点C作CH⊥x轴,交于点H,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBH=90°,
∵∠ABO+∠OAB=90°,
∴∠OAB=∠CBH,
∴ AOB BHC,
∴BH=OA=6,CH=OB=3,
∴OH=9,
∴C(9,3)
∵反比例函数在第一象限的图象经过正方形的顶点C,
∴k=9×3=27,
∴;
(2)如图所示,过点D作轴,,,
同(1)方法可得:,
∵,
∴四边形OGEA为矩形,
∴AO=EG=6,DE=OB=3,AE=AO=6,
∴D(6,9),
∵点A’恰好落在反比例函数图象上,
∴当y=6时,x=,
∴m=,
∴D’(6+,9)即D’(,9);
(3)当OA’=OP时,如图所示:
∵A’(,6),
OA’=,
四边形OPQA’是菱形,
A’Q∥OP,A’Q=OP,
Q(12,6),
当点Q’在第二象限时,Q’(-3,6);
当A’O=A’P时,如图所示:
点A’与点Q关于x轴对称,
Q(,-6);
当PO=PA’时,如图设P(m,0),
则PO=PA’,
∴,
解得:,
∴OP=A’Q=,
∴Q(,6),
综上可得:Q(,6)或(,-6)或(12,6)或(-3,6) .
【点睛】题目主要考查反比例函数的性质,正方形的性质,平移的性质,全等三角形的判定和性质,菱形的性质,等腰三角形的性质等,理解题意,(3)中根据等腰三角形进行分类讨论是解题关键.
29.(1);
(2)8
(3)能
【分析】(1)分类讨论当时或当时,分别设函数解析式,代入求值即可;
(2)分类讨论当时或当时,分别不等式即可求解;
(3)分类讨论当时或当时,分别不等式即可求解;
【详解】(1)解:根据题意可知:
当时,设与的函数解析式为,
∴,
解得:,
∴;
当时,设与的函数解析式为,
∴,
解得:
∴
综上所述,该商品上市以后销售量y(万件)与时间x(天数)之间的表达式为:;.
(2)解:当时,
令,
解得:,
∴,
∴销量不到36万件的天数为8天;
当时,
令,
解得: (不符合题意),
∴上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数为8天;
(3)解:当时,
令,
解得:
∴,
∴销量超过100万件的天数为6天,
当时,
令,
解得:
∴,
销量超过100万件的天数为6天,
综上所述,销售量不低于100万件,并且持续天数为12天,广告设计师可以拿到“特殊贡献奖”.
【点睛】本题考查了分段函数的实际运用,把握正比函数、反比例函数的图像及性质和运用分类讨论思想是解决本题的关键.
30.(1)
(2),
(3)存在,点、的坐标为、或、或P(-7,0)、Q(-3,-2).
【分析】(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,由正方形的性质结合同角的余角相等即可证出△ADE≌△BAF,从而得出DE=AF,AE=BF,再结合点A、D的坐标即可求出点B的坐标;
(2)设反比例函数为,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
【详解】(1)解:(1)过点作轴于点,过点作轴于点,如图1所示.
∵四边形为正方形,
∴,,
∵,,
∴.
在和中,
,
∴,
∴,.
∵点,,
∴,,
∴点的坐标为,即.
故答案为:.
(2)设反比例函数为,
由题意得:点坐标为,点坐标为,
∵点和在该比例函数图象上,
∴,
解得:,,
∴反比例函数解析式为.
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,).
以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:
①B′D′为对角线时,
∵四边形B′PD′Q为平行四边形,
∴,
解得:,
∴P(,0),Q(,4);
②当B′D′为边时.
∵四边形PQB′D′为平行四边形,
∴,
解得:,
∴P(7,0),Q(3,2);
∵四边形B′QPD′为平行四边形,
∴,
解得:.
∴P(-7,0)、Q(-3,-2).
综上可知:存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形,
符合题意的点P、Q的坐标为:P(,0)、Q(,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).
【点睛】本题考查了反比例函数图象上点的坐标特征、正方形的性质、全等三角形的判定及性质、平行四边形的性质以及解方程组,解题的关键是:(1)证出△ADE≌△BAF;(2)找出关于k、t的二元一次方程组;(3)分类讨论.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,利用反比例函数图形上点的坐标表示出来反比例函数系数k是关键.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
