第四单元第2课时《解比例》精品课件(共20张ppt) 人教版 数学 六年级下册
文档属性
| 名称 | 第四单元第2课时《解比例》精品课件(共20张ppt) 人教版 数学 六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 972.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 17:20:23 | ||
图片预览





文档简介
(共20张PPT)
解比例
第四单元 比例
学习目标
理解解比例的含义,学会解比例的方法,进一步掌握比例的基本性质。
重点
通过合作交流,提高分析问题和解决问题的能力。
联系生活实际,学会利用解比例的方法解决一些实际问题。
创设情境
复习旧知
上节课我们学习了什么?
我们学习了比例。
我们还知道了比例的基本性质。
创设情境
练习回顾
8∶6 =( )∶30
=
( )
20
3.2
8
想一想,你打算怎么求括号中的数?
可以根据比例的意义,先求出一个比的比值,再根据这个比值求出缺少的项。
还可以用比例的基本性质,算出两个外项或两个内项的积,再根据这个积求缺少的项。
创设情境
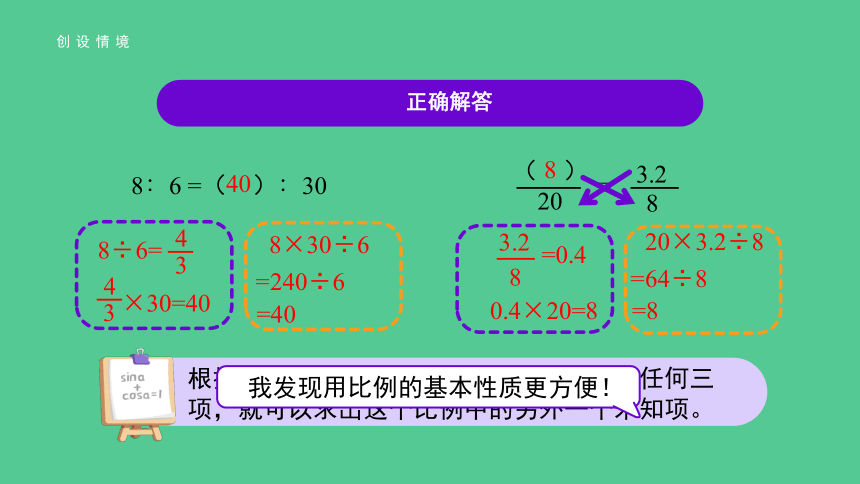
正确解答
8∶6 =( )∶30
=
( )
20
3.2
8
8÷6=
4
3
×30=40
4
3
8×30÷6
=240÷6
=40
40
=0.4
3.2
8
0.4×20=8
20×3.2÷8
=64÷8
=8
8
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
我发现用比例的基本性质更方便!
探索解比例的方法
探究新知
=
( )
20
3.2
8
8∶6 = ∶30
( )
x
x
求比例中的未知项,叫做解比例。
解比例时,根据比例的基本性质,先将比例转化成方程,然后再解未知数。
探究新知
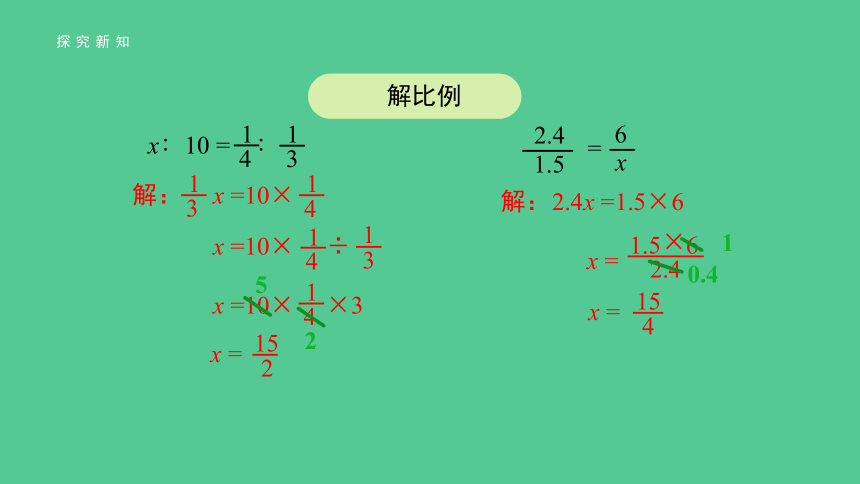
解比例
=
1.5
6
x
2.4
x∶10 = ∶
1
3
1
4
解:
x =10×
1
3
1
4
x =10× ÷
1
4
1
3
x =10× ×3
1
4
x =
15
2
解:
2.4x =1.5×6
x =
1.5 6
2.4
×
x =
15
4
5
2
1
0.4
探究新知
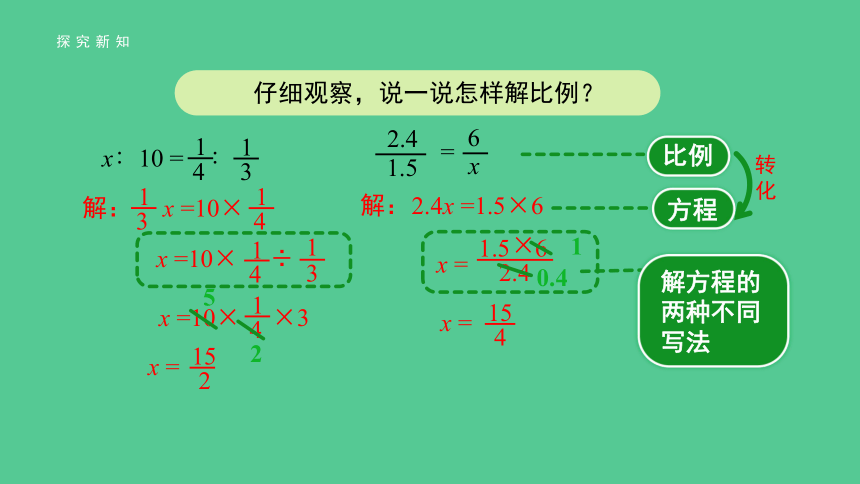
仔细观察,说一说怎样解比例?
=
1.5
6
x
2.4
x∶10 = ∶
1
3
1
4
解:
x =10×
1
3
1
4
x =10× ÷
1
4
1
3
x =10× ×3
1
4
x =
15
2
解:
2.4x =1.5×6
x =
1.5 6
2.4
×
x =
15
4
5
2
1
0.4
比例
方程
解方程的两种不同写法
转化
探究新知
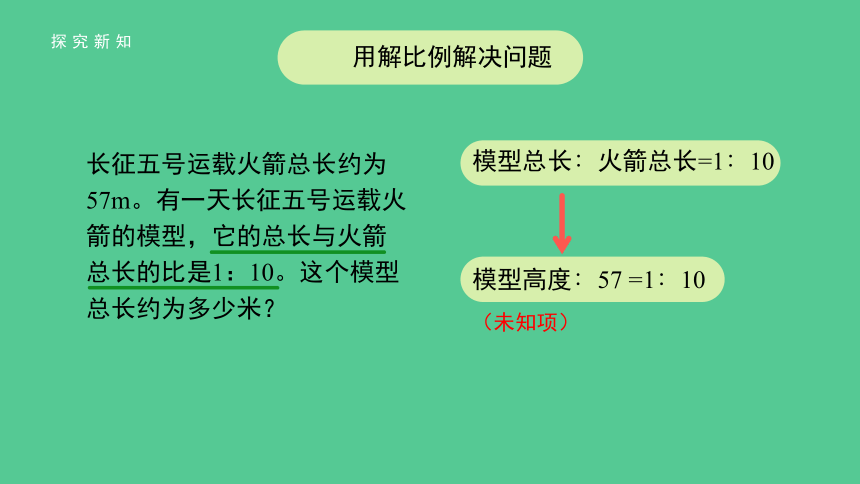
用解比例解决问题
长征五号运载火箭总长约为57m。有一天长征五号运载火箭的模型,它的总长与火箭总长的比是1:10。这个模型总长约为多少米?
模型总长∶火箭总长=1∶10
模型高度∶57 =1∶10
(未知项)
探究新知
用解比例解决问题
长征五号运载火箭总长约为57m。有一天长征五号运载火箭的模型,它的总长与火箭总长的比是1:10。这个模型总长约为多少米?
解:设这座模型高 x m。
x∶57 = 1∶10
10 x = 57×1
x = 57÷10
x = 5.7
答:这座模型高5.7 m。
检验: 5.7∶57
=(5.7÷10)∶(57÷10)
= 1∶10
探究新知
解:设这座模型高 x m。
x∶57 = 1∶10
10 x = 57×1
x = 57÷10
x = 5.7
答:这座模型高5.7 m。
检验: 5.7∶57
=(5.7÷10)∶(57÷10)
= 1∶10
检验 代入比例进行检验。
列式 根据题意列出比例。
转化 根据比例的基本性质,
把比例转化成方程。
解答 解方程,求出未知项的值。
巩固新知
(1)0.4∶x = 1.2∶2
(2)=
解:1.2x = 0.4×2
x =
2
3
x =
0.4×2
1.2
1
3
解:12x = 2.4×3
x =
2.4×3
12
x =0.6
0.6
1
1
1.解比例
x = 10
x = 12-2
解:
5(x +2)= 10×6
x +2 = 10×6÷5
x +2 = 12
(3)=
巩固新知
2. 餐馆给餐具消毒,要用100 mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入水多少毫升?
消毒液∶水=1∶150
100∶水=1∶150
100∶x = 1∶150
解:设应加入水 x mL。
x = 100×150
x = 15000
答:应加入水15000 mL。
检验:
100∶15000
= 1∶150
巩固新知
2. 餐馆给餐具消毒,要用100 mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入水多少毫升?
想一想:如果100 mL是水,那么需要加入多少毫升的消毒液?
这个问题的比例该怎么列呢?
巩固新知
2. 餐馆给餐具消毒,要用100 mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入水多少毫升?
想一想:如果100 mL是水,那么需要加入多少毫升的消毒液?
消毒液∶水=1∶150
消毒液∶100=1∶150
x∶100 = 1∶150
用解比例解决问题一定要理清比例各项的位置顺序。
巩固新知
3.侦探柯南之神秘脚印
柯南在一次案发现场测得一名犯罪嫌疑人的脚印长25 cm,根据这个脚印,他很快判断出了犯罪嫌疑人的身高。你知道他是怎样判断的吗?
科学研究表明:人体身高与脚长的比大约是7∶1。
解:犯罪嫌疑人的身高为x cm。
x∶25 = 7∶1
答:犯罪嫌疑人的身高为175 cm。
x = 25×7
x = 175
课堂小结
今天的学习你有什么收获?
解比例:
先将比例转化成方程,再解未知数。
解比例解决问题:
列式→转化→解答→检验
拓展延伸
骡行七里马行九,先放骡行七里走,次后马走赶骡行,几里相随一处有?
根据时间=,列出比例求解。
解:设追上时马行x 里。
=
答:追上时马行31.5里。
7x = 9×(x7)
x = 31.5
课后活动
同桌之间相互出几道解比例的题目,试着算一算吧!
再见
解比例
第四单元 比例
学习目标
理解解比例的含义,学会解比例的方法,进一步掌握比例的基本性质。
重点
通过合作交流,提高分析问题和解决问题的能力。
联系生活实际,学会利用解比例的方法解决一些实际问题。
创设情境
复习旧知
上节课我们学习了什么?
我们学习了比例。
我们还知道了比例的基本性质。
创设情境
练习回顾
8∶6 =( )∶30
=
( )
20
3.2
8
想一想,你打算怎么求括号中的数?
可以根据比例的意义,先求出一个比的比值,再根据这个比值求出缺少的项。
还可以用比例的基本性质,算出两个外项或两个内项的积,再根据这个积求缺少的项。
创设情境
正确解答
8∶6 =( )∶30
=
( )
20
3.2
8
8÷6=
4
3
×30=40
4
3
8×30÷6
=240÷6
=40
40
=0.4
3.2
8
0.4×20=8
20×3.2÷8
=64÷8
=8
8
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
我发现用比例的基本性质更方便!
探索解比例的方法
探究新知
=
( )
20
3.2
8
8∶6 = ∶30
( )
x
x
求比例中的未知项,叫做解比例。
解比例时,根据比例的基本性质,先将比例转化成方程,然后再解未知数。
探究新知
解比例
=
1.5
6
x
2.4
x∶10 = ∶
1
3
1
4
解:
x =10×
1
3
1
4
x =10× ÷
1
4
1
3
x =10× ×3
1
4
x =
15
2
解:
2.4x =1.5×6
x =
1.5 6
2.4
×
x =
15
4
5
2
1
0.4
探究新知
仔细观察,说一说怎样解比例?
=
1.5
6
x
2.4
x∶10 = ∶
1
3
1
4
解:
x =10×
1
3
1
4
x =10× ÷
1
4
1
3
x =10× ×3
1
4
x =
15
2
解:
2.4x =1.5×6
x =
1.5 6
2.4
×
x =
15
4
5
2
1
0.4
比例
方程
解方程的两种不同写法
转化
探究新知
用解比例解决问题
长征五号运载火箭总长约为57m。有一天长征五号运载火箭的模型,它的总长与火箭总长的比是1:10。这个模型总长约为多少米?
模型总长∶火箭总长=1∶10
模型高度∶57 =1∶10
(未知项)
探究新知
用解比例解决问题
长征五号运载火箭总长约为57m。有一天长征五号运载火箭的模型,它的总长与火箭总长的比是1:10。这个模型总长约为多少米?
解:设这座模型高 x m。
x∶57 = 1∶10
10 x = 57×1
x = 57÷10
x = 5.7
答:这座模型高5.7 m。
检验: 5.7∶57
=(5.7÷10)∶(57÷10)
= 1∶10
探究新知
解:设这座模型高 x m。
x∶57 = 1∶10
10 x = 57×1
x = 57÷10
x = 5.7
答:这座模型高5.7 m。
检验: 5.7∶57
=(5.7÷10)∶(57÷10)
= 1∶10
检验 代入比例进行检验。
列式 根据题意列出比例。
转化 根据比例的基本性质,
把比例转化成方程。
解答 解方程,求出未知项的值。
巩固新知
(1)0.4∶x = 1.2∶2
(2)=
解:1.2x = 0.4×2
x =
2
3
x =
0.4×2
1.2
1
3
解:12x = 2.4×3
x =
2.4×3
12
x =0.6
0.6
1
1
1.解比例
x = 10
x = 12-2
解:
5(x +2)= 10×6
x +2 = 10×6÷5
x +2 = 12
(3)=
巩固新知
2. 餐馆给餐具消毒,要用100 mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入水多少毫升?
消毒液∶水=1∶150
100∶水=1∶150
100∶x = 1∶150
解:设应加入水 x mL。
x = 100×150
x = 15000
答:应加入水15000 mL。
检验:
100∶15000
= 1∶150
巩固新知
2. 餐馆给餐具消毒,要用100 mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入水多少毫升?
想一想:如果100 mL是水,那么需要加入多少毫升的消毒液?
这个问题的比例该怎么列呢?
巩固新知
2. 餐馆给餐具消毒,要用100 mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入水多少毫升?
想一想:如果100 mL是水,那么需要加入多少毫升的消毒液?
消毒液∶水=1∶150
消毒液∶100=1∶150
x∶100 = 1∶150
用解比例解决问题一定要理清比例各项的位置顺序。
巩固新知
3.侦探柯南之神秘脚印
柯南在一次案发现场测得一名犯罪嫌疑人的脚印长25 cm,根据这个脚印,他很快判断出了犯罪嫌疑人的身高。你知道他是怎样判断的吗?
科学研究表明:人体身高与脚长的比大约是7∶1。
解:犯罪嫌疑人的身高为x cm。
x∶25 = 7∶1
答:犯罪嫌疑人的身高为175 cm。
x = 25×7
x = 175
课堂小结
今天的学习你有什么收获?
解比例:
先将比例转化成方程,再解未知数。
解比例解决问题:
列式→转化→解答→检验
拓展延伸
骡行七里马行九,先放骡行七里走,次后马走赶骡行,几里相随一处有?
根据时间=,列出比例求解。
解:设追上时马行x 里。
=
答:追上时马行31.5里。
7x = 9×(x7)
x = 31.5
课后活动
同桌之间相互出几道解比例的题目,试着算一算吧!
再见
