第五单元 第5课时 三角形的内角和(教学课件)-四年级数学下册 人教版(共39张PPT)
文档属性
| 名称 | 第五单元 第5课时 三角形的内角和(教学课件)-四年级数学下册 人教版(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 17:54:49 | ||
图片预览







文档简介
(共39张PPT)
第5课时 三角形的内角和
小学数学·四年级(下)·RJ
在学生动手获取知识的过程中,渗透“转化”的数学思想,培养学生的创新意识、实践能力和运用新知解决问题的能力。
通过量、剪、拼等活动,发现并验证三角形的内角和是180°。
在探究过程中积累数学活动经验,激发学习数学的兴趣。
探索和发现“三角形的内角和是180°”这一规律。
对不同探索方法进行指导,学生能灵活应用发现的规律。
理解并掌握三角形的内角和是180°,渗透转化思想,为今后学习图形知识打下基础。培养了学生与他人合作的能力。
我的个头最大,我的内角和一定比你们大!
我有一个钝角,我的内角和才是最大的!
我不服气,
咱们来比比!
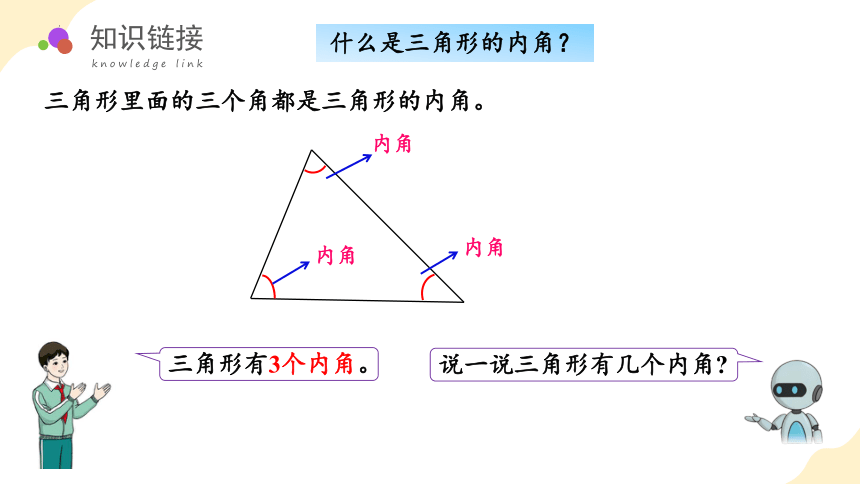
三角形有3个内角。
说一说三角形有几个内角
内角
什么是三角形的内角?
三角形里面的三个角都是三角形的内角。
内角
内角
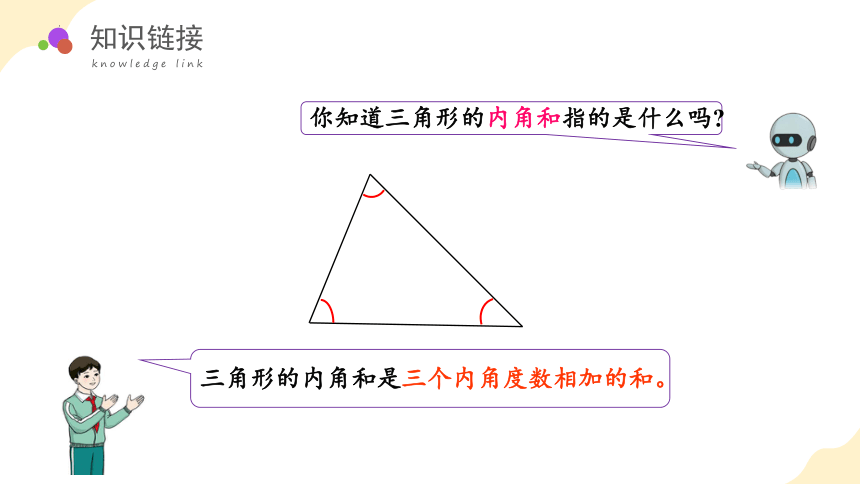
三角形的内角和是三个内角度数相加的和。
你知道三角形的内角和指的是什么吗
探究不同三角形的内角和
30°
60°
90°
45°
90°
45°
你知道三角尺内角的度数分别是多少吗?
每个三角尺的内角度
数之和都是180°。
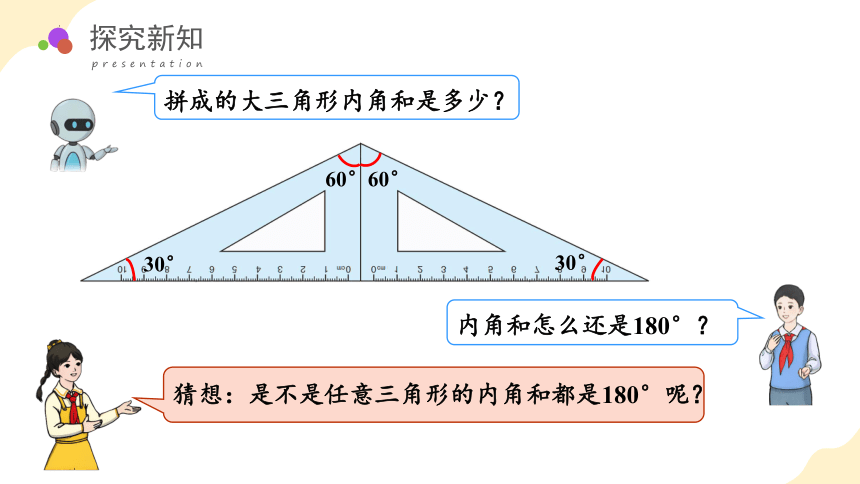
30°
30°
60°
60°
拼成的大三角形内角和是多少?
内角和怎么还是180°?
猜想:是不是任意三角形的内角和都是180°呢?
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
先画出三种不同类型的三角形
1
2
3
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
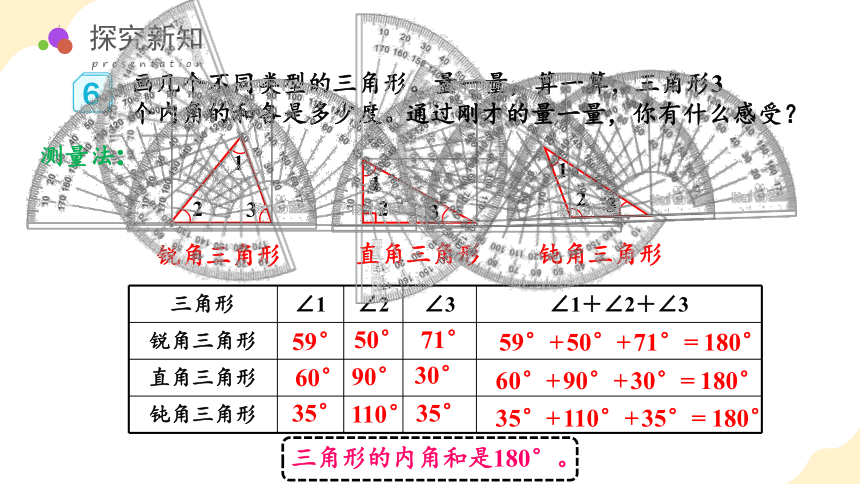
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
三角形 ∠1 ∠2 ∠3 ∠1+∠2+∠3
锐角三角形
直角三角形
钝角三角形
59°
50°
71°
59°+50°+71°=180°
60°
90°
30°
60°+90°+30°=180°
35°
110°
35°
35°+110°+35°=180°
通过刚才的量一量,你有什么感受?
测量法:
三角形的内角和是180°。
∠1+∠2+∠3
=
平角
2
1
3
2
锐角三角形
将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
剪拼法:
三角形的内角和是180°。
直角三角形
∠1+∠2+∠3 = 平角= 180°
2
2
3
1
将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
剪拼法:
三角形的内角和是180°。
钝角三角形
∠1+∠2+∠3 = 平角= 180°
2
1
3
1
将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
剪拼法:
三角形的内角和是180°。
1
把∠1、∠2和∠3都向内折,使它们的顶点都落在底边的一个点上。
2
1
3
3
锐角三角形
2
∠1+∠2+∠3
平角
= 180°
=
按照下面的方法折一折,你发现了什么?
折拼法:
三角形的内角和是180°。
1
1
2
2
3
3
直角三角形
把∠1、∠2和∠3都向内折,使它们的顶点都落在底边的一个点上。
∠1+∠2+∠3 = 平角= 180°
按照下面的方法折一折,你发现了什么?
折拼法:
三角形的内角和是180°。
1
1
2
2
3
3
钝角三角形
把∠1、∠2和∠3都向内折,使它们的顶点都落在底边的一个点上。
∠1+∠2+∠3 = 平角= 180°
按照下面的方法折一折,你发现了什么?
折拼法:
三角形的内角和是180°。
三角形的内角和是180°。
三角形的内角和
有多种方法可以求证三角形的内角和:
量一量
折一折
拼一拼
介绍数学文化
帕斯卡与三角形的内角和
帕斯卡,法国数学家。早在300多年前这位科学家就已经发现了任何三角形的内角和是180度,而他当时才12 岁。
帕斯卡没有受过正规的学校教育,4岁时母亲病故,由父亲和两个姐姐负责对他进行教育和培养。帕斯卡的父亲认为学习数学很伤身体,所以把家里所有的数学书都藏了起来,并且不允许他的朋友们在帕斯卡面前谈论数学。他只让帕斯卡看古典文学书,希望他能好好学习文学。父亲这一做法反而引起了帕斯卡对数学的兴趣。他开始偷偷地研究数学。
有一天他问父亲,什么是几何?父亲很简单地回答说“几何就是教人在画图时能作出正确又美观的图”。于是帕斯卡就拿了粉笔在地上画起各种图形来。画着画着,12岁的帕斯卡发现任何一个三角形内角和都是180度,当他把这个发现告诉父亲时,父亲激动得泪如雨下,搬出了自己所有的数学书给帕斯卡看。在其父精心地教育下,帕斯卡很小时就精通欧几里得几何,他自己独立地发现了欧几里得的前32条定理,而且顺序也完全正确。后来通过不断的自学探究,帕斯卡成了非常有成就的数学家、物理学家、哲学家和散文学家。
当年12岁的帕斯卡好像自言自语,又好像是告诉父亲一件重大事情似地说: “三角形三个内角的总和是两个直角。”
帕斯卡怎么证明的呢?我们一起来看看:
长方形的四个角都是直角,长方形的四个角的和一定是360°。把长方形沿对角线一分为二,就变成两个直角三角形,每个直角三角形的内角和就是360除以2等于180度。任意一个直角三角形都可以看做是长方形剪开的,所以任意直角三角形的内角和一定是180度。
任何一个锐角三角形都可以沿高分为两个直角三角形,两个直角三角形的和180+180=360度,而其中有两个直角拼在一起成了一条直线,所以真正作为锐角三角形的三个内角的和就是360-90-90=180度。同样的道理可以说明钝角三角形内角和也是180度。
帕斯卡与计算器
1642年,法国,布莱士·帕斯卡设计并制作了一台能自动进位的加减法计算装置,被称为是世界上第一台数字计算器,为以后的计算机设计提供了基本原理。
拓展延伸
有两个直角的图形不是三角形。
有两个钝角的图形不是三角形。
一个三角形中最多只有一个直角或钝角!
想一想:
1.你能画出一个有两个直角或两个钝角的三角形吗?为什么?
2.大三角形的内角和比小三角形的内角和大,对吗?为什么?
三角形的内角和与三角形的形状、大小没有关系,都是1800。
就像我们学习角大小的时候,与边长无关。
3.一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度吗?
辨析:错误地认为拼接后图形的内角和是把之前图形的内角和相加得到。
应该是 180°,因为拼完之后还是一个三角形。所以三角形的内角和与三角形的形状、大小没有关系。
三角形的内角和的度数和它的大小形状无关。
三角形,真奇怪
有胖有瘦有高矮
内角和是180度
我们时刻牢记它
达标练习,巩固成果
教材第65页做一做 第1题
1.在右图中,∠1=140°,∠3=25°。求∠2的度数。
∠1+∠2+∠3=180°
∠2=180°-∠1-∠3
=180°-140°-25°
=15°
教材第65页做一做第2题
2.把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度
因为任意一个三角形的内角和都是180°,所以沿虚线剪开后每个小三角形的内角和是180°。
3.算出下面各个未知角的度数。
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
教材第67页“练习十六”第1题
教材第67页“练习十六”第2题
4.求出下列三角形各个角的度数。
(2)(180°-96°)÷2
=84°÷2
=42°
(3)180°-90°-40°
=90°-40°
=50°
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
(3)一个直角三角形,其中一个锐角是40°。
(1)180°÷3=60°
教材第67页“练习十六”第3题
5.
爸爸给小红买了一个等腰三角形的风筝。风筝的一个底角是70°,风筝的顶角是多少度?
180°-70°-70°=40°
70°
70°
?
答:风筝的顶角是40°。
6. 小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来的一个角,另一块有原来的两个角。他想重新买一块玻璃按上去,小明非常聪明,只带了其中的一块到玻璃店去,就配了和原来一模一样的玻璃了,你知道他带的是哪一块吗?
带的是第2块,因为第2块有两个角,延长就可以还原这个三角形。
2. 三角形的内角和是180°。
1. 可以运用剪、拼或折叠的方法验证三角形的内角和。
三角形的内角和
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第5课时 三角形的内角和
小学数学·四年级(下)·RJ
在学生动手获取知识的过程中,渗透“转化”的数学思想,培养学生的创新意识、实践能力和运用新知解决问题的能力。
通过量、剪、拼等活动,发现并验证三角形的内角和是180°。
在探究过程中积累数学活动经验,激发学习数学的兴趣。
探索和发现“三角形的内角和是180°”这一规律。
对不同探索方法进行指导,学生能灵活应用发现的规律。
理解并掌握三角形的内角和是180°,渗透转化思想,为今后学习图形知识打下基础。培养了学生与他人合作的能力。
我的个头最大,我的内角和一定比你们大!
我有一个钝角,我的内角和才是最大的!
我不服气,
咱们来比比!
三角形有3个内角。
说一说三角形有几个内角
内角
什么是三角形的内角?
三角形里面的三个角都是三角形的内角。
内角
内角
三角形的内角和是三个内角度数相加的和。
你知道三角形的内角和指的是什么吗
探究不同三角形的内角和
30°
60°
90°
45°
90°
45°
你知道三角尺内角的度数分别是多少吗?
每个三角尺的内角度
数之和都是180°。
30°
30°
60°
60°
拼成的大三角形内角和是多少?
内角和怎么还是180°?
猜想:是不是任意三角形的内角和都是180°呢?
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
先画出三种不同类型的三角形
1
2
3
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
三角形 ∠1 ∠2 ∠3 ∠1+∠2+∠3
锐角三角形
直角三角形
钝角三角形
59°
50°
71°
59°+50°+71°=180°
60°
90°
30°
60°+90°+30°=180°
35°
110°
35°
35°+110°+35°=180°
通过刚才的量一量,你有什么感受?
测量法:
三角形的内角和是180°。
∠1+∠2+∠3
=
平角
2
1
3
2
锐角三角形
将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
剪拼法:
三角形的内角和是180°。
直角三角形
∠1+∠2+∠3 = 平角= 180°
2
2
3
1
将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
剪拼法:
三角形的内角和是180°。
钝角三角形
∠1+∠2+∠3 = 平角= 180°
2
1
3
1
将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
剪拼法:
三角形的内角和是180°。
1
把∠1、∠2和∠3都向内折,使它们的顶点都落在底边的一个点上。
2
1
3
3
锐角三角形
2
∠1+∠2+∠3
平角
= 180°
=
按照下面的方法折一折,你发现了什么?
折拼法:
三角形的内角和是180°。
1
1
2
2
3
3
直角三角形
把∠1、∠2和∠3都向内折,使它们的顶点都落在底边的一个点上。
∠1+∠2+∠3 = 平角= 180°
按照下面的方法折一折,你发现了什么?
折拼法:
三角形的内角和是180°。
1
1
2
2
3
3
钝角三角形
把∠1、∠2和∠3都向内折,使它们的顶点都落在底边的一个点上。
∠1+∠2+∠3 = 平角= 180°
按照下面的方法折一折,你发现了什么?
折拼法:
三角形的内角和是180°。
三角形的内角和是180°。
三角形的内角和
有多种方法可以求证三角形的内角和:
量一量
折一折
拼一拼
介绍数学文化
帕斯卡与三角形的内角和
帕斯卡,法国数学家。早在300多年前这位科学家就已经发现了任何三角形的内角和是180度,而他当时才12 岁。
帕斯卡没有受过正规的学校教育,4岁时母亲病故,由父亲和两个姐姐负责对他进行教育和培养。帕斯卡的父亲认为学习数学很伤身体,所以把家里所有的数学书都藏了起来,并且不允许他的朋友们在帕斯卡面前谈论数学。他只让帕斯卡看古典文学书,希望他能好好学习文学。父亲这一做法反而引起了帕斯卡对数学的兴趣。他开始偷偷地研究数学。
有一天他问父亲,什么是几何?父亲很简单地回答说“几何就是教人在画图时能作出正确又美观的图”。于是帕斯卡就拿了粉笔在地上画起各种图形来。画着画着,12岁的帕斯卡发现任何一个三角形内角和都是180度,当他把这个发现告诉父亲时,父亲激动得泪如雨下,搬出了自己所有的数学书给帕斯卡看。在其父精心地教育下,帕斯卡很小时就精通欧几里得几何,他自己独立地发现了欧几里得的前32条定理,而且顺序也完全正确。后来通过不断的自学探究,帕斯卡成了非常有成就的数学家、物理学家、哲学家和散文学家。
当年12岁的帕斯卡好像自言自语,又好像是告诉父亲一件重大事情似地说: “三角形三个内角的总和是两个直角。”
帕斯卡怎么证明的呢?我们一起来看看:
长方形的四个角都是直角,长方形的四个角的和一定是360°。把长方形沿对角线一分为二,就变成两个直角三角形,每个直角三角形的内角和就是360除以2等于180度。任意一个直角三角形都可以看做是长方形剪开的,所以任意直角三角形的内角和一定是180度。
任何一个锐角三角形都可以沿高分为两个直角三角形,两个直角三角形的和180+180=360度,而其中有两个直角拼在一起成了一条直线,所以真正作为锐角三角形的三个内角的和就是360-90-90=180度。同样的道理可以说明钝角三角形内角和也是180度。
帕斯卡与计算器
1642年,法国,布莱士·帕斯卡设计并制作了一台能自动进位的加减法计算装置,被称为是世界上第一台数字计算器,为以后的计算机设计提供了基本原理。
拓展延伸
有两个直角的图形不是三角形。
有两个钝角的图形不是三角形。
一个三角形中最多只有一个直角或钝角!
想一想:
1.你能画出一个有两个直角或两个钝角的三角形吗?为什么?
2.大三角形的内角和比小三角形的内角和大,对吗?为什么?
三角形的内角和与三角形的形状、大小没有关系,都是1800。
就像我们学习角大小的时候,与边长无关。
3.一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度吗?
辨析:错误地认为拼接后图形的内角和是把之前图形的内角和相加得到。
应该是 180°,因为拼完之后还是一个三角形。所以三角形的内角和与三角形的形状、大小没有关系。
三角形的内角和的度数和它的大小形状无关。
三角形,真奇怪
有胖有瘦有高矮
内角和是180度
我们时刻牢记它
达标练习,巩固成果
教材第65页做一做 第1题
1.在右图中,∠1=140°,∠3=25°。求∠2的度数。
∠1+∠2+∠3=180°
∠2=180°-∠1-∠3
=180°-140°-25°
=15°
教材第65页做一做第2题
2.把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度
因为任意一个三角形的内角和都是180°,所以沿虚线剪开后每个小三角形的内角和是180°。
3.算出下面各个未知角的度数。
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
教材第67页“练习十六”第1题
教材第67页“练习十六”第2题
4.求出下列三角形各个角的度数。
(2)(180°-96°)÷2
=84°÷2
=42°
(3)180°-90°-40°
=90°-40°
=50°
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
(3)一个直角三角形,其中一个锐角是40°。
(1)180°÷3=60°
教材第67页“练习十六”第3题
5.
爸爸给小红买了一个等腰三角形的风筝。风筝的一个底角是70°,风筝的顶角是多少度?
180°-70°-70°=40°
70°
70°
?
答:风筝的顶角是40°。
6. 小明不小心将镜框上的一块三角形玻璃摔成了两半,玻璃裂成了两块。一块只有原来的一个角,另一块有原来的两个角。他想重新买一块玻璃按上去,小明非常聪明,只带了其中的一块到玻璃店去,就配了和原来一模一样的玻璃了,你知道他带的是哪一块吗?
带的是第2块,因为第2块有两个角,延长就可以还原这个三角形。
2. 三角形的内角和是180°。
1. 可以运用剪、拼或折叠的方法验证三角形的内角和。
三角形的内角和
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
