广东省深圳实验学校光明部2022-2023学年高二下学期期中考试数学试题(含答案)
文档属性
| 名称 | 广东省深圳实验学校光明部2022-2023学年高二下学期期中考试数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览




文档简介
深圳实验学校光明部2022-2023学年度第二学期期中考试
高二数学
时间:120分钟 满分:150分
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.已知两个正态分布的密度函数图像如图所示,则( )
A., B.,
C., D.,
6.邮递员把两封信随机投入A,B,C三个空邮箱中,则不同的投入方法共有( )
A.6种 B.8种 C.9种 D.10种
3.10支步枪中有6支已经校准过,4支未校准,一名射击运动员用校准过的枪射击时,中靶的概率为,用未校准的枪射击时,中靶的概率为,现从10支中任取一支射击,则中靶的概率为( )
A. B. C. D.
8.随机变量的分布列如下,则( )
0 1 2
A. B. C. D.
5.学校安排元旦晩会的4个舞蹈节目和2个音乐节目的演出顺序,要求2个音乐节目要连排,且都不能在第一个演出,则不同的排法种数是( )
A.96 B.144 C.192 D.240
10.2023年元旦期间,某高速公路收费站的三个高速收费口每天通过的小汽车数(单位:辆)服从正态分布,若,假设三个收费口均能正常工作,则这些收费口每天至少有一个通过的小汽车超过600辆的概率为( )
A. B. C. D.
7.的展开式中,的系数为( )
A.60 B.-60 C.30 D.-30
8.深圳实验学校光明部高二年级来到井冈山古城镇参加社会实践,学校安排甲、乙、丙、丁、戊共5位老师到学生居住的塘头村、沃壤村、长溪村进行走访,要求每村至少安排一位老师,则塘头村恰好只有甲老师的概率为( )
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分).
9.对两个随机变量的一组观测数据进行回归分析,下列说法正确的是( )
A.可以先用散点图判断两个变量是否具有线性相关关系
B.可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型拟合效果越好
C.可以用相关指数刻画回归效果,越接近0,说明模型的拟合效果越好
D.回归直线恒过样本点的中心
10.已知,则( )
A. B.
C.展开式中所有二项式系数的和为1024 D.
11.将5个质地和大小均相同的小球分装在甲、乙两个口袋中,甲袋中装有1个黑球和1个白球,乙袋中装有2个黑球和1个白球.采用不放回抽取的方式,先从甲袋每次随机抽取一个小球,当甲袋中的1个黑球被取出后再用同一方式在乙袋中进行抽取,直到将乙袋中的2个黑球全部取出后停止.记总抽取次数为,下列说法正确的是( )
A.
B.已知从甲袋第一次就取到了黑球,则的概率为
C.
D.若把这5个球放进一个袋子里去,每次随机抽取一个球,取后不放回,记总抽取次数为,则
12.商场某区域的行走路线图可以抽象为一个的正方体道路网(如图,图中线段均为可行走的通道),甲、乙两人分别从A,B两点出发,随机地选择一条最短路径,以相同的速度同时出发,直到到达B,A为止.下列说法正确的是( )
A.甲从必须经过到达的方法数共有9种
B.甲从A到的方法数共有90种
C.甲、乙两人在处相遇的概率为
D.甲、乙两人相遇的概率为
三、填空题(本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上).
13.二项式的展开式中的常数项为________.
14.甲、乙两名运动员进行乒乓球比赛,已知每局比赛甲胜的概率为,乙胜的概率为,各局比赛的胜负互不影响,现采取7局4胜制,则甲获胜且比赛局数恰好为5局的概率是________.
15.花店还剩七束花,其中三束郁金香,两束白玫瑰,两束康乃馨,李明随机选了两束,已知李明选到的两束花是同一种花,则这两束花都是郁金香的概率为________.
16.杜牧《羊栏浦夜陪安会》的诗句中“球来香袖依稀暖,酒凸觥心泛艳光”描述的是唐代酒宴上的助兴游戏“击鼓传花”,也称传彩球.游戏规则为:鼓响时,众人开始依次传花,至鼓停为止,此时花在谁手中,谁就上台表演节目.甲、乙、丙三人玩击鼓传花,鼓响时,第1次由甲将花传出,每次传花时,传花者都等可能地将花传给另外两人中的任何一人,经过8次传递后,花又在甲手中的概率为________.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)
记的内角,,的对边分别为,,.已知,,.
(1)求和的面积;
(2)点在边上,且,求.
18.(本小题满分12分)
已知数列的前项和,数列满足,且.
(1)求数列和的通项公式;
(2)设,求数列的前项和.
19.(本小题满分12分)
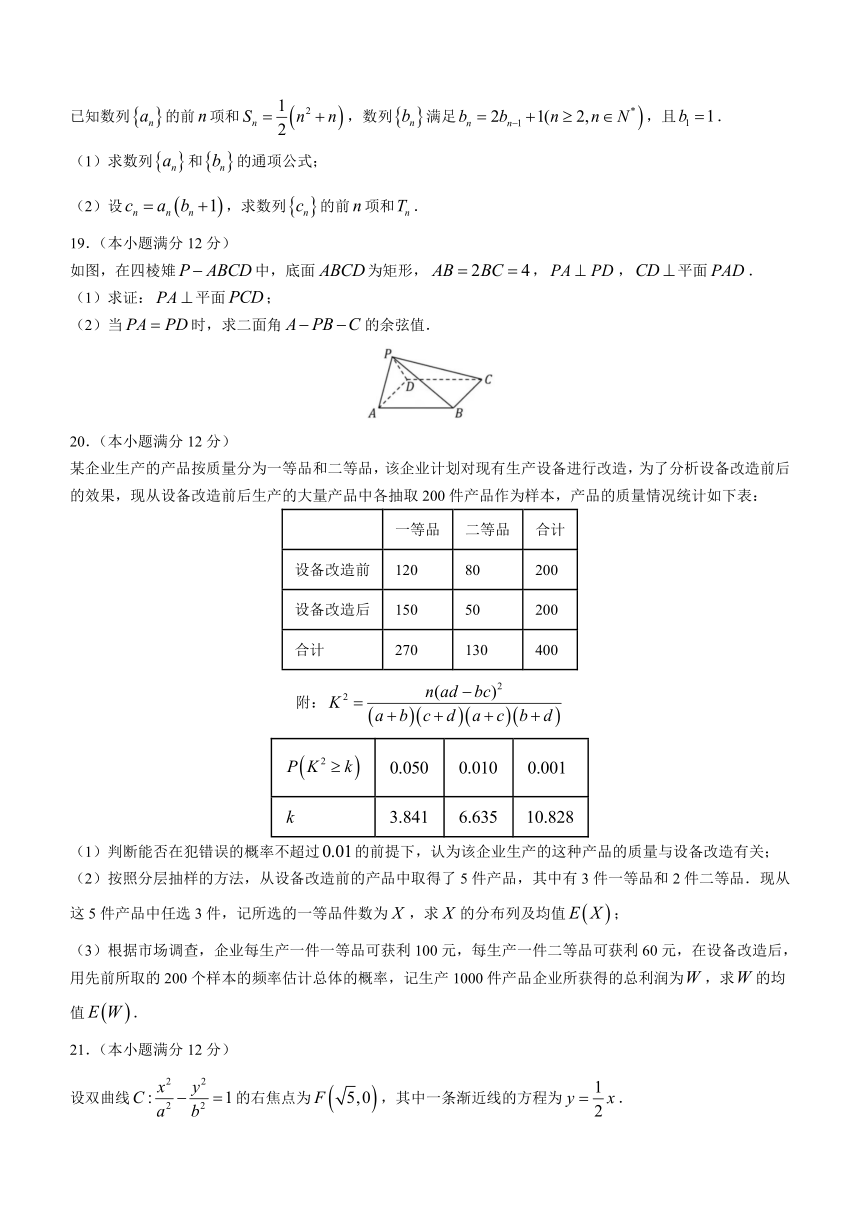
如图,在四棱雉中,底面为矩形,,,平面.
(1)求证:平面;
(2)当时,求二面角的余弦值.
20.(本小题满分12分)
某企业生产的产品按质量分为一等品和二等品,该企业计划对现有生产设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取200件产品作为样本,产品的质量情况统计如下表:
一等品 二等品 合计
设备改造前 120 80 200
设备改造后 150 50 200
合计 270 130 400
附:
(1)判断能否在犯错误的概率不超过的前提下,认为该企业生产的这种产品的质量与设备改造有关;
(2)按照分层抽样的方法,从设备改造前的产品中取得了5件产品,其中有3件一等品和2件二等品.现从这5件产品中任选3件,记所选的一等品件数为,求的分布列及均值;
(3)根据市场调查,企业每生产一件一等品可获利100元,每生产一件二等品可获利60元,在设备改造后,用先前所取的200个样本的频率估计总体的概率,记生产1000件产品企业所获得的总利润为,求的均值.
21.(本小题满分12分)
设双曲线的右焦点为,其中一条渐近线的方程为.
(1)求双曲线的方程;
(2)过点的直线与双曲线的右支交于A,B两点,过点A,B分别作直线的垂线(点A,B在直线的两侧),垂足分别为M,N,记,,的面积分别为,,,试问:是否存在常数,使得 若存在,求出的值;若不存在,请说明理由.
22.(本小题满分12分)
已知函数,圆.
(1)讨论的单调性;
(2)若,曲线与圆恰有三条公切线,求的取值范围.
深圳实验学校光明部2022-2023学年度第二学期期中考试
高二数学 答案及评分标准
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1 2 3 4 5 6 7 8
A C B D C C A B
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分).
9 10 11 12
ABD ACD AC ABD
三、填空题(本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上).
13.-160 14. 15. 16.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤).
17.(10分)
解:(1)在中,由余弦定理,
.
.
(2)在中,由余弦定理,
,
,,.
在中,由正弦定理,
.
18.(12分)
解:(1)当时,;
当时,,
,.
设,
则,,
是首项为,公比为2的等比数列,
.
所以,,.
(2),
①
②
①-②得
,
.
19.(12分)
(1)证明:平面,平面,
.
,且,,平面,
平面.
(2)解:过点作,垂足为.
平面,平面,
,
又,.
取中点,分别以OA,OM,OP为轴,轴,轴建立空间直角坐标系,如图所示,
在等腰中,,.
,,,,,
设平面的一个法向量为,
,,
,令,得,,
设平面的一个法向量为,
,,
,令,得,,.
.
注意到二面角的平面角为针角,
二面角的余弦值为.
20.(12分)
解:(1)零假设为:质量指标值与设备改造无关.
,
不成立,故能在犯错误的概率不超过的前提下,认为该企业生产的这种产品的质量指标值与设备改造有关;
(2).
,
,
,
的分布列为
1 2 3
.
(3)设生产的一等品有件,则二等品有件,
,
,
,
元
21.(12分)
解:(1)由题意:
(2)设,,则,.
设直线,
由得
,与右支交于2点,或
,.
,,.
.
即.
22.(12分)
解:(1),.
(1)当时,,在单调递增.
(2)当时,,,
在单调递增,在单调递减.
综上所述,当时,在单调递增;
当时,在单调递增,在单调递减.
(2),,设切点为,则切线方程:,即.
直线与圆相切,,
令,则在有3个根.
设
(1)若,即,,,
在单调递增,
,当时,,
当时,有1根.
(2)若,即,,
,
令,,单调递增,且.
当时,,单调递减;当时,,单调递增.
.
又,,当时,,(或
在和分别有2根.
综上,.
高二数学
时间:120分钟 满分:150分
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.已知两个正态分布的密度函数图像如图所示,则( )
A., B.,
C., D.,
6.邮递员把两封信随机投入A,B,C三个空邮箱中,则不同的投入方法共有( )
A.6种 B.8种 C.9种 D.10种
3.10支步枪中有6支已经校准过,4支未校准,一名射击运动员用校准过的枪射击时,中靶的概率为,用未校准的枪射击时,中靶的概率为,现从10支中任取一支射击,则中靶的概率为( )
A. B. C. D.
8.随机变量的分布列如下,则( )
0 1 2
A. B. C. D.
5.学校安排元旦晩会的4个舞蹈节目和2个音乐节目的演出顺序,要求2个音乐节目要连排,且都不能在第一个演出,则不同的排法种数是( )
A.96 B.144 C.192 D.240
10.2023年元旦期间,某高速公路收费站的三个高速收费口每天通过的小汽车数(单位:辆)服从正态分布,若,假设三个收费口均能正常工作,则这些收费口每天至少有一个通过的小汽车超过600辆的概率为( )
A. B. C. D.
7.的展开式中,的系数为( )
A.60 B.-60 C.30 D.-30
8.深圳实验学校光明部高二年级来到井冈山古城镇参加社会实践,学校安排甲、乙、丙、丁、戊共5位老师到学生居住的塘头村、沃壤村、长溪村进行走访,要求每村至少安排一位老师,则塘头村恰好只有甲老师的概率为( )
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分).
9.对两个随机变量的一组观测数据进行回归分析,下列说法正确的是( )
A.可以先用散点图判断两个变量是否具有线性相关关系
B.可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型拟合效果越好
C.可以用相关指数刻画回归效果,越接近0,说明模型的拟合效果越好
D.回归直线恒过样本点的中心
10.已知,则( )
A. B.
C.展开式中所有二项式系数的和为1024 D.
11.将5个质地和大小均相同的小球分装在甲、乙两个口袋中,甲袋中装有1个黑球和1个白球,乙袋中装有2个黑球和1个白球.采用不放回抽取的方式,先从甲袋每次随机抽取一个小球,当甲袋中的1个黑球被取出后再用同一方式在乙袋中进行抽取,直到将乙袋中的2个黑球全部取出后停止.记总抽取次数为,下列说法正确的是( )
A.
B.已知从甲袋第一次就取到了黑球,则的概率为
C.
D.若把这5个球放进一个袋子里去,每次随机抽取一个球,取后不放回,记总抽取次数为,则
12.商场某区域的行走路线图可以抽象为一个的正方体道路网(如图,图中线段均为可行走的通道),甲、乙两人分别从A,B两点出发,随机地选择一条最短路径,以相同的速度同时出发,直到到达B,A为止.下列说法正确的是( )
A.甲从必须经过到达的方法数共有9种
B.甲从A到的方法数共有90种
C.甲、乙两人在处相遇的概率为
D.甲、乙两人相遇的概率为
三、填空题(本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上).
13.二项式的展开式中的常数项为________.
14.甲、乙两名运动员进行乒乓球比赛,已知每局比赛甲胜的概率为,乙胜的概率为,各局比赛的胜负互不影响,现采取7局4胜制,则甲获胜且比赛局数恰好为5局的概率是________.
15.花店还剩七束花,其中三束郁金香,两束白玫瑰,两束康乃馨,李明随机选了两束,已知李明选到的两束花是同一种花,则这两束花都是郁金香的概率为________.
16.杜牧《羊栏浦夜陪安会》的诗句中“球来香袖依稀暖,酒凸觥心泛艳光”描述的是唐代酒宴上的助兴游戏“击鼓传花”,也称传彩球.游戏规则为:鼓响时,众人开始依次传花,至鼓停为止,此时花在谁手中,谁就上台表演节目.甲、乙、丙三人玩击鼓传花,鼓响时,第1次由甲将花传出,每次传花时,传花者都等可能地将花传给另外两人中的任何一人,经过8次传递后,花又在甲手中的概率为________.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)
记的内角,,的对边分别为,,.已知,,.
(1)求和的面积;
(2)点在边上,且,求.
18.(本小题满分12分)
已知数列的前项和,数列满足,且.
(1)求数列和的通项公式;
(2)设,求数列的前项和.
19.(本小题满分12分)
如图,在四棱雉中,底面为矩形,,,平面.
(1)求证:平面;
(2)当时,求二面角的余弦值.
20.(本小题满分12分)
某企业生产的产品按质量分为一等品和二等品,该企业计划对现有生产设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取200件产品作为样本,产品的质量情况统计如下表:
一等品 二等品 合计
设备改造前 120 80 200
设备改造后 150 50 200
合计 270 130 400
附:
(1)判断能否在犯错误的概率不超过的前提下,认为该企业生产的这种产品的质量与设备改造有关;
(2)按照分层抽样的方法,从设备改造前的产品中取得了5件产品,其中有3件一等品和2件二等品.现从这5件产品中任选3件,记所选的一等品件数为,求的分布列及均值;
(3)根据市场调查,企业每生产一件一等品可获利100元,每生产一件二等品可获利60元,在设备改造后,用先前所取的200个样本的频率估计总体的概率,记生产1000件产品企业所获得的总利润为,求的均值.
21.(本小题满分12分)
设双曲线的右焦点为,其中一条渐近线的方程为.
(1)求双曲线的方程;
(2)过点的直线与双曲线的右支交于A,B两点,过点A,B分别作直线的垂线(点A,B在直线的两侧),垂足分别为M,N,记,,的面积分别为,,,试问:是否存在常数,使得 若存在,求出的值;若不存在,请说明理由.
22.(本小题满分12分)
已知函数,圆.
(1)讨论的单调性;
(2)若,曲线与圆恰有三条公切线,求的取值范围.
深圳实验学校光明部2022-2023学年度第二学期期中考试
高二数学 答案及评分标准
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1 2 3 4 5 6 7 8
A C B D C C A B
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分).
9 10 11 12
ABD ACD AC ABD
三、填空题(本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上).
13.-160 14. 15. 16.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤).
17.(10分)
解:(1)在中,由余弦定理,
.
.
(2)在中,由余弦定理,
,
,,.
在中,由正弦定理,
.
18.(12分)
解:(1)当时,;
当时,,
,.
设,
则,,
是首项为,公比为2的等比数列,
.
所以,,.
(2),
①
②
①-②得
,
.
19.(12分)
(1)证明:平面,平面,
.
,且,,平面,
平面.
(2)解:过点作,垂足为.
平面,平面,
,
又,.
取中点,分别以OA,OM,OP为轴,轴,轴建立空间直角坐标系,如图所示,
在等腰中,,.
,,,,,
设平面的一个法向量为,
,,
,令,得,,
设平面的一个法向量为,
,,
,令,得,,.
.
注意到二面角的平面角为针角,
二面角的余弦值为.
20.(12分)
解:(1)零假设为:质量指标值与设备改造无关.
,
不成立,故能在犯错误的概率不超过的前提下,认为该企业生产的这种产品的质量指标值与设备改造有关;
(2).
,
,
,
的分布列为
1 2 3
.
(3)设生产的一等品有件,则二等品有件,
,
,
,
元
21.(12分)
解:(1)由题意:
(2)设,,则,.
设直线,
由得
,与右支交于2点,或
,.
,,.
.
即.
22.(12分)
解:(1),.
(1)当时,,在单调递增.
(2)当时,,,
在单调递增,在单调递减.
综上所述,当时,在单调递增;
当时,在单调递增,在单调递减.
(2),,设切点为,则切线方程:,即.
直线与圆相切,,
令,则在有3个根.
设
(1)若,即,,,
在单调递增,
,当时,,
当时,有1根.
(2)若,即,,
,
令,,单调递增,且.
当时,,单调递减;当时,,单调递增.
.
又,,当时,,(或
在和分别有2根.
综上,.
同课章节目录
