第2章 整式加减 单元同步检测试题 人教版七年级数学上册(含答案)
文档属性
| 名称 | 第2章 整式加减 单元同步检测试题 人教版七年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 137.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 08:11:30 | ||
图片预览


文档简介
第二章《整式加减》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列说法中,正确的是( )
A.不是整式 B.﹣的系数是﹣3,次数是3
C.3是单项式 D.多项式2x2y﹣xy是五次二项式
2.东北大米每千克售价为x元,苏北大米每千克售价为y元,取东北大米a千克和苏北大米b千克混合,要使混合前后大米的总售价不变,则混合后的大米每千克售价为 ( )
A. B. C. D.
3.如果,那么代数式的值是()
A.0 B.2 C.5 D.8
5.下列运算中,正确的是( )
A.3a+2b=5ab B.2a3+3a2=5a5 C.3a2b-3ba2=0 D.5a2-4a2=1
6.下面的计算正确的是( )
A.2a3﹣a3=a3 B.a2+a3=a5 C.2a+2b=2ab D.4a﹣3a=1
7.将﹣2(a﹣b)去括号得到的结果是( )
A.﹣2a+b B.﹣2a﹣b C.﹣2a+2b D.﹣2a﹣2b
8.已知2xn+1y3与x4y3是同类项,则n的值是( )
A.2 B.3 C.4 D.5
9.下列运算中,正确的是( )
A.3a+b=3ab B.﹣3a2﹣2a2=﹣5a4
C.﹣2(x﹣4)=﹣2x﹣4 D.﹣3a2b+2a2b=﹣a2b
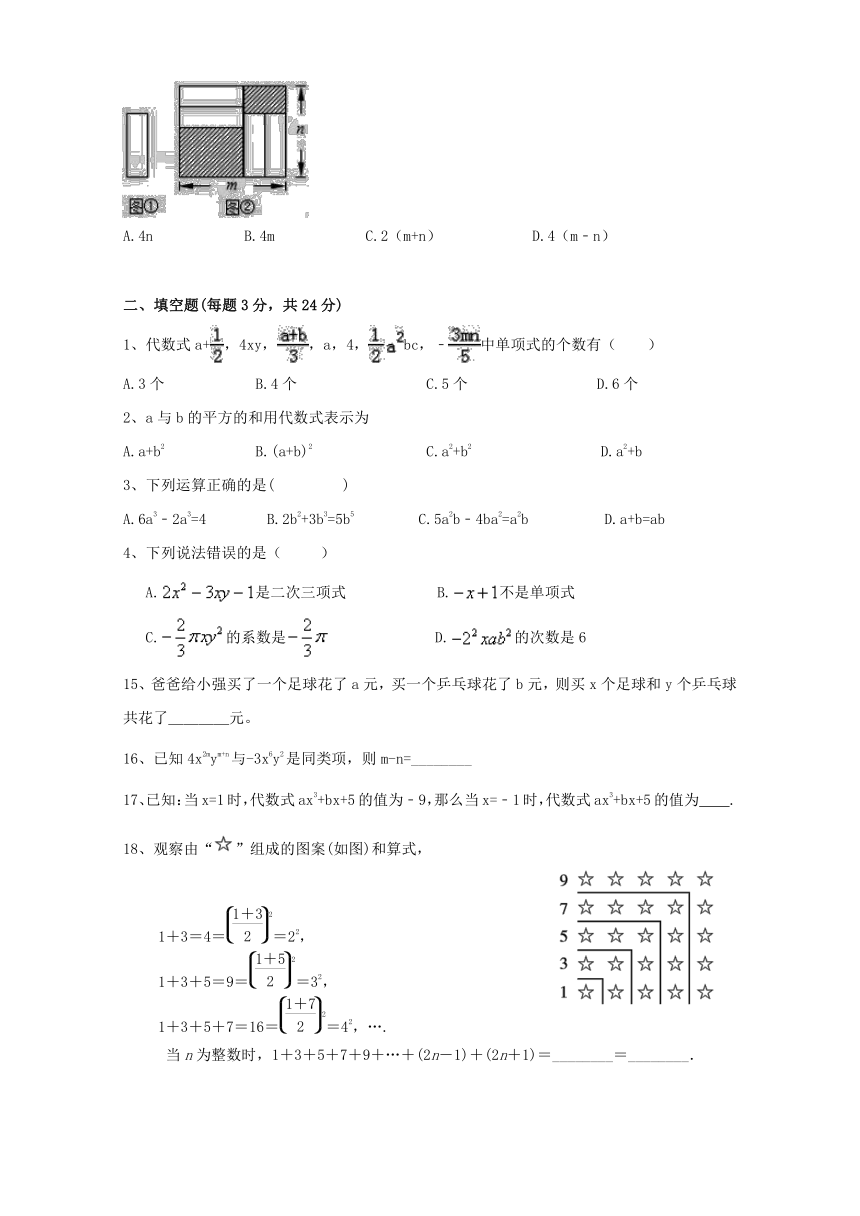
10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n )的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )
A.4n B.4m C.2(m+n) D.4(m﹣n)
二、填空题(每题3分,共24分)
1、代数式a+,4xy,,a,4,bc,﹣中单项式的个数有( )
A.3个 B.4个 C.5个 D.6个
2、a与b的平方的和用代数式表示为
A.a+b2 B.(a+b)2 C.a2+b2 D.a2+b
3、下列运算正确的是( )
A.6a3﹣2a3=4 B.2b2+3b3=5b5 C.5a2b﹣4ba2=a2b D.a+b=ab
4、下列说法错误的是( )
A.是二次三项式 B.不是单项式
C.的系数是 D.的次数是6
15、爸爸给小强买了一个足球花了a元,买一个乒乓球花了b元,则买x个足球和y个乒乓球共花了____元。
16、已知4x2mym+n与-3x6y2是同类项,则m-n=________
17、已知:当x=1时,代数式ax3+bx+5的值为﹣9,那么当x=﹣1时,代数式ax3+bx+5的值为 .
18、观察由“”组成的图案(如图)和算式,
1+3=4==22,
1+3+5=9==32,
1+3+5+7=16==42,….
当n为整数时,1+3+5+7+9+…+(2n-1)+(2n+1)=________=________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.化简:
(1)(5a2+2a﹣1)﹣4[3﹣2(4a+a2)].
(2)3x2﹣[7x﹣(4x﹣3)﹣2x2].
20.先化简,再求值:2ab+6(a2b+ab2)﹣[3a2b﹣2(1﹣ab﹣2ab2)],其中a为最大的负整数,b为最小的正整数.
21.已知数轴上点A,O,P所表示的数分别是﹣3,0,x点P在线段AO上.
(1)请在数轴上标出A,O两点;
(2)①线段AP= (用含x的式子表示)
②在点P右侧的数轴上画线段PQ=AP,当OP=2OQ时,求x的值.
22.已知关于x,y的多项式x4+(m+2)xny-xy2+3,其中n为正整数.
(1)当m,n为何值时,它是五次四项式?
(2)当m,n为何值时,它是四次三项式?
23、某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
(1)用字母和π的式子表示阴影部分的面积;
(2)当m=8,n=6,a=1,b=2时,阴影部分的面积是多少?(π取3)
24、有这样一道题“求多项式a2b3﹣ab+b2﹣(4a2b3﹣ab﹣b2)+(3a2b3+ab)﹣5的值,
其中a=2,b=﹣3”.马小虎做题时把a=2错抄成a=﹣2,但他做出的结果却是正确的,
你知道这是怎么回事吗?请说明理由,并求出结果.
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C D C A C B D B
二.填空题
11. 【答案】3 [解析] 因为(a2+2kab)+(b2-6ab)= a2+2kab+b2-6ab=a2+ b2+(2k-6)ab,又多项式a2+2kab与b2-6ab的和不含ab项,所以2k-6=0.所以k=3.
12. 【答案】4 -5x4 4 -1
13.解:根据题意得:3m2+m﹣1+3m=3m2+4m﹣1.
故答案为:3m2+4m﹣1.
14.解:∵3anbn﹣1与﹣5a2b2m(m是正整数)是同类项,
∴n=2,2m=n﹣1,
∴2m=1,
∴(2m﹣1)2=02=0.
故答案为:0.
15、
16、4;
17、 19 .
18、;(n+1)2
三.解答题
19.解:(1)原式=5a2+2a﹣1﹣[12﹣8(4a+a2)]=5a2+2a﹣1﹣12+8(4a+a2)=5a2+2a﹣1﹣12+32a+8a2=13a2+34a﹣13;
(2)原式=3x2﹣7x+(4x﹣3)+2x2=3x2﹣7x+4x﹣3+2x2=5x2﹣3x﹣3.
20.解:原式=2ab+3a2b+6ab2﹣3a2b+2﹣2ab﹣4ab2
=(2ab﹣2ab)+2+(3a2b﹣3a2b)+(6ab2﹣4ab2)
=2ab2+2,
∵a为最大的负整数,b为最小的正整数,
∴a=﹣1,b=1,
∴原式=2×(﹣1)×1+2
=0.
21.解:(1)如图所示:
(2)①线段AP=x+3;
②情况一:当点Q在点O的左侧时,如图:
∵AP=PQ,
∴AQ=2AP=2(x+3)=2x+6,
OQ=OA﹣AQ=3﹣(2x+6)=﹣2x﹣3,
OP=﹣x,
OP=2OQ,
﹣x=2(﹣2x﹣3),
x=﹣2.
情况二:当点Q在点O右侧时,如图:
此时OQ=AQ﹣OA=(2x+6)﹣3=2x+3,
OP=2OQ,
﹣x=2(2x+3),
.
综上,x的值为﹣2或.
故答案为:x+3.
22.解:(1)因为多项式是五次四项式,
所以n+1=5,m+2≠0,
所以n=4,m≠-2.
(2)因为多项式是四次三项式,
所以m+2=0,n为任意正整数,
所以m=-2,n为任意正整数.
23、(1)mn﹣πb2﹣4ab;
(2)当m=8,n=6,a=1,b=2时,mn﹣πb2﹣4ab=8×6﹣3×22﹣4×1×2=48﹣12﹣8=28
24、解:∵a2b3﹣ab+b2﹣(4a2b3﹣ab﹣b2)+(3a2b3+ab)﹣5
=a2b3﹣ab+b2﹣4a2b3+ab+b2+3a2b3+ab﹣5=2b2﹣5,∴此整式化简后与a的值无关,
∴马小虎做题时把a=2错抄成a=﹣2,但他做出的结果却是正确的.
当b=﹣3时,原式=2×(﹣3)2﹣5=13.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列说法中,正确的是( )
A.不是整式 B.﹣的系数是﹣3,次数是3
C.3是单项式 D.多项式2x2y﹣xy是五次二项式
2.东北大米每千克售价为x元,苏北大米每千克售价为y元,取东北大米a千克和苏北大米b千克混合,要使混合前后大米的总售价不变,则混合后的大米每千克售价为 ( )
A. B. C. D.
3.如果,那么代数式的值是()
A.0 B.2 C.5 D.8
5.下列运算中,正确的是( )
A.3a+2b=5ab B.2a3+3a2=5a5 C.3a2b-3ba2=0 D.5a2-4a2=1
6.下面的计算正确的是( )
A.2a3﹣a3=a3 B.a2+a3=a5 C.2a+2b=2ab D.4a﹣3a=1
7.将﹣2(a﹣b)去括号得到的结果是( )
A.﹣2a+b B.﹣2a﹣b C.﹣2a+2b D.﹣2a﹣2b
8.已知2xn+1y3与x4y3是同类项,则n的值是( )
A.2 B.3 C.4 D.5
9.下列运算中,正确的是( )
A.3a+b=3ab B.﹣3a2﹣2a2=﹣5a4
C.﹣2(x﹣4)=﹣2x﹣4 D.﹣3a2b+2a2b=﹣a2b
10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n )的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )
A.4n B.4m C.2(m+n) D.4(m﹣n)
二、填空题(每题3分,共24分)
1、代数式a+,4xy,,a,4,bc,﹣中单项式的个数有( )
A.3个 B.4个 C.5个 D.6个
2、a与b的平方的和用代数式表示为
A.a+b2 B.(a+b)2 C.a2+b2 D.a2+b
3、下列运算正确的是( )
A.6a3﹣2a3=4 B.2b2+3b3=5b5 C.5a2b﹣4ba2=a2b D.a+b=ab
4、下列说法错误的是( )
A.是二次三项式 B.不是单项式
C.的系数是 D.的次数是6
15、爸爸给小强买了一个足球花了a元,买一个乒乓球花了b元,则买x个足球和y个乒乓球共花了____元。
16、已知4x2mym+n与-3x6y2是同类项,则m-n=________
17、已知:当x=1时,代数式ax3+bx+5的值为﹣9,那么当x=﹣1时,代数式ax3+bx+5的值为 .
18、观察由“”组成的图案(如图)和算式,
1+3=4==22,
1+3+5=9==32,
1+3+5+7=16==42,….
当n为整数时,1+3+5+7+9+…+(2n-1)+(2n+1)=________=________.
三.解答题(共46分,19题6分,20 ---24题8分)
19.化简:
(1)(5a2+2a﹣1)﹣4[3﹣2(4a+a2)].
(2)3x2﹣[7x﹣(4x﹣3)﹣2x2].
20.先化简,再求值:2ab+6(a2b+ab2)﹣[3a2b﹣2(1﹣ab﹣2ab2)],其中a为最大的负整数,b为最小的正整数.
21.已知数轴上点A,O,P所表示的数分别是﹣3,0,x点P在线段AO上.
(1)请在数轴上标出A,O两点;
(2)①线段AP= (用含x的式子表示)
②在点P右侧的数轴上画线段PQ=AP,当OP=2OQ时,求x的值.
22.已知关于x,y的多项式x4+(m+2)xny-xy2+3,其中n为正整数.
(1)当m,n为何值时,它是五次四项式?
(2)当m,n为何值时,它是四次三项式?
23、某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
(1)用字母和π的式子表示阴影部分的面积;
(2)当m=8,n=6,a=1,b=2时,阴影部分的面积是多少?(π取3)
24、有这样一道题“求多项式a2b3﹣ab+b2﹣(4a2b3﹣ab﹣b2)+(3a2b3+ab)﹣5的值,
其中a=2,b=﹣3”.马小虎做题时把a=2错抄成a=﹣2,但他做出的结果却是正确的,
你知道这是怎么回事吗?请说明理由,并求出结果.
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C D C A C B D B
二.填空题
11. 【答案】3 [解析] 因为(a2+2kab)+(b2-6ab)= a2+2kab+b2-6ab=a2+ b2+(2k-6)ab,又多项式a2+2kab与b2-6ab的和不含ab项,所以2k-6=0.所以k=3.
12. 【答案】4 -5x4 4 -1
13.解:根据题意得:3m2+m﹣1+3m=3m2+4m﹣1.
故答案为:3m2+4m﹣1.
14.解:∵3anbn﹣1与﹣5a2b2m(m是正整数)是同类项,
∴n=2,2m=n﹣1,
∴2m=1,
∴(2m﹣1)2=02=0.
故答案为:0.
15、
16、4;
17、 19 .
18、;(n+1)2
三.解答题
19.解:(1)原式=5a2+2a﹣1﹣[12﹣8(4a+a2)]=5a2+2a﹣1﹣12+8(4a+a2)=5a2+2a﹣1﹣12+32a+8a2=13a2+34a﹣13;
(2)原式=3x2﹣7x+(4x﹣3)+2x2=3x2﹣7x+4x﹣3+2x2=5x2﹣3x﹣3.
20.解:原式=2ab+3a2b+6ab2﹣3a2b+2﹣2ab﹣4ab2
=(2ab﹣2ab)+2+(3a2b﹣3a2b)+(6ab2﹣4ab2)
=2ab2+2,
∵a为最大的负整数,b为最小的正整数,
∴a=﹣1,b=1,
∴原式=2×(﹣1)×1+2
=0.
21.解:(1)如图所示:
(2)①线段AP=x+3;
②情况一:当点Q在点O的左侧时,如图:
∵AP=PQ,
∴AQ=2AP=2(x+3)=2x+6,
OQ=OA﹣AQ=3﹣(2x+6)=﹣2x﹣3,
OP=﹣x,
OP=2OQ,
﹣x=2(﹣2x﹣3),
x=﹣2.
情况二:当点Q在点O右侧时,如图:
此时OQ=AQ﹣OA=(2x+6)﹣3=2x+3,
OP=2OQ,
﹣x=2(2x+3),
.
综上,x的值为﹣2或.
故答案为:x+3.
22.解:(1)因为多项式是五次四项式,
所以n+1=5,m+2≠0,
所以n=4,m≠-2.
(2)因为多项式是四次三项式,
所以m+2=0,n为任意正整数,
所以m=-2,n为任意正整数.
23、(1)mn﹣πb2﹣4ab;
(2)当m=8,n=6,a=1,b=2时,mn﹣πb2﹣4ab=8×6﹣3×22﹣4×1×2=48﹣12﹣8=28
24、解:∵a2b3﹣ab+b2﹣(4a2b3﹣ab﹣b2)+(3a2b3+ab)﹣5
=a2b3﹣ab+b2﹣4a2b3+ab+b2+3a2b3+ab﹣5=2b2﹣5,∴此整式化简后与a的值无关,
∴马小虎做题时把a=2错抄成a=﹣2,但他做出的结果却是正确的.
当b=﹣3时,原式=2×(﹣3)2﹣5=13.
