19.2.2 一次函数(3) 课件(共30张PPT)
文档属性
| 名称 | 19.2.2 一次函数(3) 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 20:36:28 | ||
图片预览











文档简介
(共30张PPT)
19.2.2一次函数(3)
人教版八年级下册
知识回顾
1.回顾一次函数的概念和性质.
2.直线y=2x-3与x轴的交点坐标为__________,与y轴的交点坐标为___________,图象经过_____________象限,y随x的增大而_______.
(0,-3)
一、三、四
增大
教学目标
1.掌握用待定系数法求函数解析式的方法.
2.会熟练运用待定系数法在函数的实际应用中.
新知导入
1. 我们画出y=3x与y=3x+1的图象至少选取几个点,为什么?
2. 思考:如果已知一次函数图象上的两点,那么能确定它的解析式吗?
两点确定一条直线——两点法
新知探究
例1. 已知一次函数的图象过点 (3, 5) 与点 (-4, -9),求这个一次函数的解析式.
分析:求一次函数y=kx+b的解析式,关键是求出k,b的值,从已知条件可以列出关于k,b的二元一次方程组,并求出k,b
因为点(3, 5) 与点 (-4, -9)在函数图象上,则这两点的坐标一定适合解析式
新知探究
例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
把点(3,5)与(-4,-9)分别代入,得:
3k+b=5
-4k+b=-9
解方程组得
y=2x-1.
∴这个一次函数的解析式为
k=2
b=-1
一设
二列
三解
四写
新知探究
像上面那样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出这个式子的方法,叫做待定系数法.
由于一次函数y=kx+b中有k和b两个待定系数,因此用待定系数法时需要根据两个条件列二元一次方程组(以k和b为未知数).解方程组后就能具体写出一次函数的解析式.
1.待定系数法
新知探究
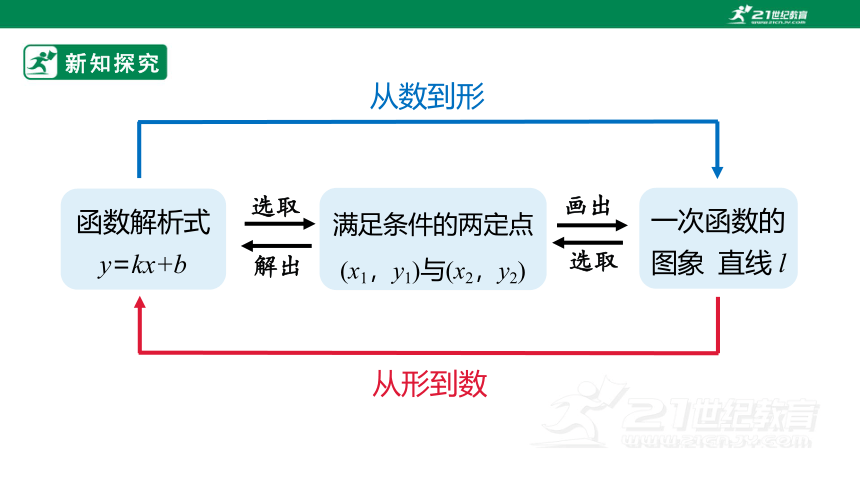
函数解析式
y=kx+b
满足条件的两定点(x1,y1)与(x2,y2)
一次函数的图象 直线 l
选取
解出
选取
画出
从数到形
从形到数
新知探究
用待定系数法求一次函数解析式的步骤
设:设出一次函数的解析式 y=kx+b(k≠0).
列:将已知的两组x、y的对应值分别代入所设的解析式 中,列出关于k、b的二元一次方程组.
解:解所列的方程组,求出k 、b的值.
代:将求出的k 、b的值代入所设解析式中,得到所求一次函数的解析式.
1
2
3
4
新知练习
1. 已知一次函数的图象过点 (9, 0) 与点 (24, 20),写出函数解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0) .
因为y=kx+b的图象过点 (9, 0) 与点 (24, 20),所以
解方程组得
这个一次函数解析式为
新知探究
2. 已知一次函数y=kx+b(k≠0)的图象与y=2x平行,且过点(2, -1),求这个一次函数的解析式.
分析:通过前面的学习,我们知道求解一次函数的解析式需要两个点,而本题中只有一个点,但是还有一个条件是y=kx+b(k≠0)和y=2x的图象是平行的,因此k=2 .
新知探究
这个一次函数解析式为y=2x-5.
∴k=2 ,
解:∵一次函数y=kx+b(k≠0)的图象与y=2x平行
∵y=kx+b的图象过点 (2, -1),代入得-1=2×2+b
解得b=-5
2. 已知一次函数y=kx+b(k≠0)的图象与y=2x平行,且过点(2, -1),求这个一次函数的解析式.
新知探究
例2. 一次函数y=kx+b(k≠0)的图象过点 A(3, 0),与 y 轴交于 B 点. 若△ABC的面积为 6,求这个一次函数的解析式.
分析:题中只确定了B点在 y 轴上,但是没有指定B点是在 y 轴的正半轴还是负半轴,因此,会分为两种情况:
A
B
O
A
B
O
新知探究
从而,B点坐标为(0, 4)或(0, -4), 再根据 A 点和 B点坐标, 利用待定系数法,就可以求解一次函数的解析式.
分析:只要根据题中所给的S△A0B=6和OA=3,求得OB=4
A
B
O
A
B
O
新知探究
解:∵ A 点坐标为(3, 0),则OA=3
∴OB=4
当B点在 y 轴正半轴时,坐标为(0, 4)
解得
因此
将 A (3, 0) 代入y=kx+4 得:0=3k+4
∴ b = 4
∵S△A0B==6
A
B
O
新知探究
当B点在 y 轴负半轴时,坐标为(0, -4)
则 b=-4
将 A (3, 0) 代入y=kx-4, 得:0=3k-4
解得
因此
综上所述,这个一次函数的解析式为
或
A
B
O
新知探究
2.一次函数的简单应用
例3 “黄金1号”玉米种子的价格为 5 元/kg,如果一次购买 2kg 以上的种子,超过 2kg 部分的种子价格打 8 折.
(1)填写表:
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4
付款金额/元
2.5
5
7.5
10
12
14
16
18
新知探究
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
分析:付款金额与种子价格相关,问题中种子价格不是固定不变的,它与购买量有关.设购买 x kg 种子,当 0≤x≤2 时,种子价格为 5元/kg;当 x>2 时,其中有 2kg 种子按 5元/kg 计价,其余的(x-2)kg(即超出 2kg 部分)种子按 4元/kg(即8折)计价.因此,写函数解析式与画函数图象时,应对 0≤x≤2 和 x>2 分段讨论.
新知探究
(2)设购买量为 x kg,付款金额为 y 元.
当 0≤x≤2 时,y=5x.
当 x>2时,y=4(x-2)+10=4x+2.
函数图象如图所示.
y 与 x 的函数解析式也可以合起来表示为
新知练习
3. 一个有进水管与出水管的容器,从某时刻开始 4min 内只进水不出水,在随后的 8min 内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量 y(单位:L)与时间 x(单位:min)之间的关系如图所示.
当0 ≤x≤ 4 时,求 y 关于 x 的函数解析式.
当0 <x≤4 时,求 y 关于 x 的函数解析式.
每分钟进水、出水各多少升?
新知练习
分析:(1) 在0 ≤x≤ 4时,图象显示为一条过原点的线段,可推断出在该范围内 y 是 x 的正比例函数,设函数解析式为y=k1x(k1≠0)代入点 求解即可;
(2) 在4 <x≤12 时,图象显示为一条线段,可推断出在该范围内 y 是 x 的一次函数,设函数解析式为y=k2x+b(k2≠0)代入点 求解即可;
(4, 20)
(4, 20) 和(12, 30)
新知探究
解:(1) 设0 ≤x≤ 4 时, y 关于 x 的函数解析式为y=k1x(k1≠0)
∵这段图象过点(4, 20)
∴20=4k1
解得 k1=5
因此在0 ≤x≤ 4时, y 关于 x 的函数解析式为y=5x
新知探究
(2) 设4 <x≤12时, y 关于 x 的函数解析式为b(≠0)
∵这段图象所在直线过点 (4, 20) 与点 (12, 30)
解方程组得
因此在 4 <x≤12 时, y 关于 x 的函数解析式为
∴
新知探究
(3) 前4分钟只进水不出水,每分钟进水量:
在4 <x≤12时,同时进水和出水,每分钟出水量用 表示,
由题意得:
答:每分钟的进水量为 5 L/min,出水量为L/min.
课堂总结
一次函数解析式
待定系数法
应用
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
①设;②列;③解;④代.
步骤
①已知一次函数解析式
②题目中未给出一次函数解析式
课堂练习
1.已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b,
因为函数图象过点 (9,0)和(24,20),
解得:
k=
b=-12
函数解析式为y= x-12
0=9k+b,
20=24k+b,
所以得:
课堂练习
2.已知一次函数y=kx+b的图象与y=x平行,且过点(1,2),那么它必过点( )
A.(-1,0) B.(2,-1)
C.(2,1) D.(0,-1)
3.已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,则此一次函数的解析式为______________________.
A
y=x+2或y=-x+2
课堂练习
4.如图,一次函数的图象与x轴和y轴分别相交于A,B两点,如果点A的坐标为(2,0),且OA=OB,求这个一次函数的解析式.
解:∵OA=OB,点A的坐标为(2,0),
∴点B的坐标为(0,-2).
设这个一次函数的解析式为y=kx+b.
将A,B两点的坐标代入解析式,得
∴这个一次函数的解析式为y=x-2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
19.2.2一次函数(3)
人教版八年级下册
知识回顾
1.回顾一次函数的概念和性质.
2.直线y=2x-3与x轴的交点坐标为__________,与y轴的交点坐标为___________,图象经过_____________象限,y随x的增大而_______.
(0,-3)
一、三、四
增大
教学目标
1.掌握用待定系数法求函数解析式的方法.
2.会熟练运用待定系数法在函数的实际应用中.
新知导入
1. 我们画出y=3x与y=3x+1的图象至少选取几个点,为什么?
2. 思考:如果已知一次函数图象上的两点,那么能确定它的解析式吗?
两点确定一条直线——两点法
新知探究
例1. 已知一次函数的图象过点 (3, 5) 与点 (-4, -9),求这个一次函数的解析式.
分析:求一次函数y=kx+b的解析式,关键是求出k,b的值,从已知条件可以列出关于k,b的二元一次方程组,并求出k,b
因为点(3, 5) 与点 (-4, -9)在函数图象上,则这两点的坐标一定适合解析式
新知探究
例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
把点(3,5)与(-4,-9)分别代入,得:
3k+b=5
-4k+b=-9
解方程组得
y=2x-1.
∴这个一次函数的解析式为
k=2
b=-1
一设
二列
三解
四写
新知探究
像上面那样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出这个式子的方法,叫做待定系数法.
由于一次函数y=kx+b中有k和b两个待定系数,因此用待定系数法时需要根据两个条件列二元一次方程组(以k和b为未知数).解方程组后就能具体写出一次函数的解析式.
1.待定系数法
新知探究
函数解析式
y=kx+b
满足条件的两定点(x1,y1)与(x2,y2)
一次函数的图象 直线 l
选取
解出
选取
画出
从数到形
从形到数
新知探究
用待定系数法求一次函数解析式的步骤
设:设出一次函数的解析式 y=kx+b(k≠0).
列:将已知的两组x、y的对应值分别代入所设的解析式 中,列出关于k、b的二元一次方程组.
解:解所列的方程组,求出k 、b的值.
代:将求出的k 、b的值代入所设解析式中,得到所求一次函数的解析式.
1
2
3
4
新知练习
1. 已知一次函数的图象过点 (9, 0) 与点 (24, 20),写出函数解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0) .
因为y=kx+b的图象过点 (9, 0) 与点 (24, 20),所以
解方程组得
这个一次函数解析式为
新知探究
2. 已知一次函数y=kx+b(k≠0)的图象与y=2x平行,且过点(2, -1),求这个一次函数的解析式.
分析:通过前面的学习,我们知道求解一次函数的解析式需要两个点,而本题中只有一个点,但是还有一个条件是y=kx+b(k≠0)和y=2x的图象是平行的,因此k=2 .
新知探究
这个一次函数解析式为y=2x-5.
∴k=2 ,
解:∵一次函数y=kx+b(k≠0)的图象与y=2x平行
∵y=kx+b的图象过点 (2, -1),代入得-1=2×2+b
解得b=-5
2. 已知一次函数y=kx+b(k≠0)的图象与y=2x平行,且过点(2, -1),求这个一次函数的解析式.
新知探究
例2. 一次函数y=kx+b(k≠0)的图象过点 A(3, 0),与 y 轴交于 B 点. 若△ABC的面积为 6,求这个一次函数的解析式.
分析:题中只确定了B点在 y 轴上,但是没有指定B点是在 y 轴的正半轴还是负半轴,因此,会分为两种情况:
A
B
O
A
B
O
新知探究
从而,B点坐标为(0, 4)或(0, -4), 再根据 A 点和 B点坐标, 利用待定系数法,就可以求解一次函数的解析式.
分析:只要根据题中所给的S△A0B=6和OA=3,求得OB=4
A
B
O
A
B
O
新知探究
解:∵ A 点坐标为(3, 0),则OA=3
∴OB=4
当B点在 y 轴正半轴时,坐标为(0, 4)
解得
因此
将 A (3, 0) 代入y=kx+4 得:0=3k+4
∴ b = 4
∵S△A0B==6
A
B
O
新知探究
当B点在 y 轴负半轴时,坐标为(0, -4)
则 b=-4
将 A (3, 0) 代入y=kx-4, 得:0=3k-4
解得
因此
综上所述,这个一次函数的解析式为
或
A
B
O
新知探究
2.一次函数的简单应用
例3 “黄金1号”玉米种子的价格为 5 元/kg,如果一次购买 2kg 以上的种子,超过 2kg 部分的种子价格打 8 折.
(1)填写表:
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4
付款金额/元
2.5
5
7.5
10
12
14
16
18
新知探究
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
分析:付款金额与种子价格相关,问题中种子价格不是固定不变的,它与购买量有关.设购买 x kg 种子,当 0≤x≤2 时,种子价格为 5元/kg;当 x>2 时,其中有 2kg 种子按 5元/kg 计价,其余的(x-2)kg(即超出 2kg 部分)种子按 4元/kg(即8折)计价.因此,写函数解析式与画函数图象时,应对 0≤x≤2 和 x>2 分段讨论.
新知探究
(2)设购买量为 x kg,付款金额为 y 元.
当 0≤x≤2 时,y=5x.
当 x>2时,y=4(x-2)+10=4x+2.
函数图象如图所示.
y 与 x 的函数解析式也可以合起来表示为
新知练习
3. 一个有进水管与出水管的容器,从某时刻开始 4min 内只进水不出水,在随后的 8min 内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量 y(单位:L)与时间 x(单位:min)之间的关系如图所示.
当0 ≤x≤ 4 时,求 y 关于 x 的函数解析式.
当0 <x≤4 时,求 y 关于 x 的函数解析式.
每分钟进水、出水各多少升?
新知练习
分析:(1) 在0 ≤x≤ 4时,图象显示为一条过原点的线段,可推断出在该范围内 y 是 x 的正比例函数,设函数解析式为y=k1x(k1≠0)代入点 求解即可;
(2) 在4 <x≤12 时,图象显示为一条线段,可推断出在该范围内 y 是 x 的一次函数,设函数解析式为y=k2x+b(k2≠0)代入点 求解即可;
(4, 20)
(4, 20) 和(12, 30)
新知探究
解:(1) 设0 ≤x≤ 4 时, y 关于 x 的函数解析式为y=k1x(k1≠0)
∵这段图象过点(4, 20)
∴20=4k1
解得 k1=5
因此在0 ≤x≤ 4时, y 关于 x 的函数解析式为y=5x
新知探究
(2) 设4 <x≤12时, y 关于 x 的函数解析式为b(≠0)
∵这段图象所在直线过点 (4, 20) 与点 (12, 30)
解方程组得
因此在 4 <x≤12 时, y 关于 x 的函数解析式为
∴
新知探究
(3) 前4分钟只进水不出水,每分钟进水量:
在4 <x≤12时,同时进水和出水,每分钟出水量用 表示,
由题意得:
答:每分钟的进水量为 5 L/min,出水量为L/min.
课堂总结
一次函数解析式
待定系数法
应用
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
①设;②列;③解;④代.
步骤
①已知一次函数解析式
②题目中未给出一次函数解析式
课堂练习
1.已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b,
因为函数图象过点 (9,0)和(24,20),
解得:
k=
b=-12
函数解析式为y= x-12
0=9k+b,
20=24k+b,
所以得:
课堂练习
2.已知一次函数y=kx+b的图象与y=x平行,且过点(1,2),那么它必过点( )
A.(-1,0) B.(2,-1)
C.(2,1) D.(0,-1)
3.已知一次函数y=kx+b(k≠0)的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,则此一次函数的解析式为______________________.
A
y=x+2或y=-x+2
课堂练习
4.如图,一次函数的图象与x轴和y轴分别相交于A,B两点,如果点A的坐标为(2,0),且OA=OB,求这个一次函数的解析式.
解:∵OA=OB,点A的坐标为(2,0),
∴点B的坐标为(0,-2).
设这个一次函数的解析式为y=kx+b.
将A,B两点的坐标代入解析式,得
∴这个一次函数的解析式为y=x-2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
