集合(山东省临沂市沂水县)
图片预览






文档简介
课件16张PPT。集合的基本运算(一) 引入考查下列各个集合,你能说出集合C与集合A、 B
之间的关系吗?(1) A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};(2) A={x|x是有理数},B={ x|x是无理数},
C={ x|x是实数};集合A、 B与集合C之间都具有这样一种关系:集合C是由集合A或集合B的元素组成的。一,并集一般地,由所有属于集合A或属于集合B的元素所
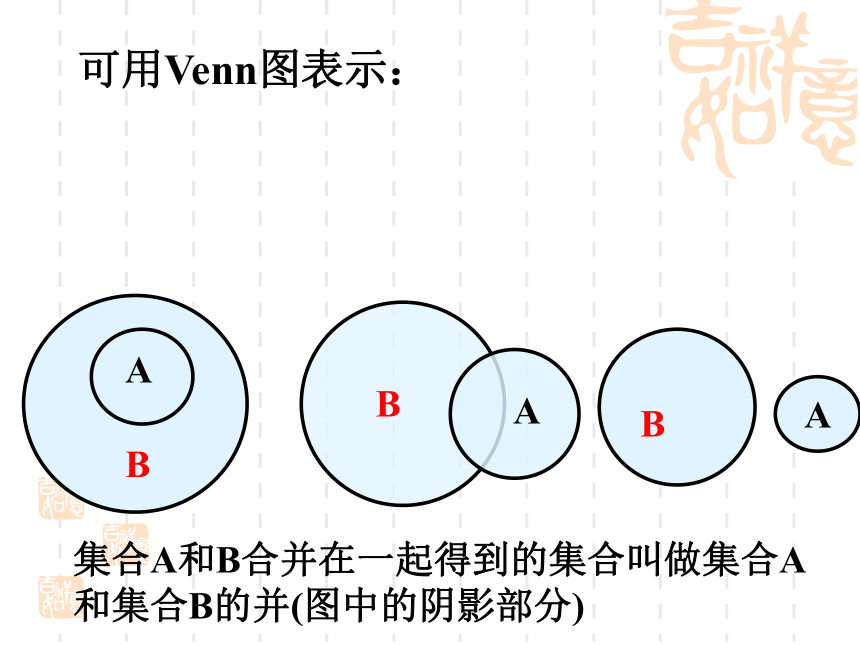
组成的集合,叫做A,B的并集.记作:A∪B(读作"A并B"),即A∪B={x|x∈A,或x∈B}.如:{1,2,3,6}∪{1,2,5,10}={1,2,3,5,6,10}.可用Venn图表示:ABBA集合A和B合并在一起得到的集合叫做集合A
和集合B的并(图中的阴影部分)BA1。 设A={4,5,6,8}, B={3,5,7,8},求A∪B.2。 设集合A={x|x为等腰三角形},集合B={x|x为直角三角形} 求A∪B.练习考察下列各个集合,你能说出集合A、 B与集合C之
间的关系吗?(1) A={2,4,6,8,10},B={3,5,8,12},C={8};(2) A={x|x是沂水四中在校的女生},
B={ x|x是沂水四中在校的高一学生}
C={ x|x是沂水四中在校的高一女生}集合A、 B与集合C之间都具有这样一种关系:集合C是有那些既属于集合A且属于集合B的所
有元素组成的二,交集一般地,由所有属于A且属于B的元素所组成的
集合,叫做A,B的交集.记作A∩B(读作"A交B"),即A∩B={x|x∈A,且x∈B}.如:{1,2,3,6}∩{1,2,5,10}={1,2}.
又如:A={a,b,c,d,e},B={c,d,e,f}.则A∩B={c,d,e}.可用Venn图表示:BABA如上图,集合A和B的公共部分叫做集合A和集合
B的交(图1的阴影部分)1。 新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学},
求A∩B.练习3. 交集的性质4.并集的性质例题分析2.设 ,
若 ,求实数m的取值范围。例题分析3.设集合 ,
且 ,求实数a的取值范围变式:设 ,
又 ,求实数a,b和c
的值。例题分析例题分析课堂小结并集
交集
交集、并集的性质
之间的关系吗?(1) A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};(2) A={x|x是有理数},B={ x|x是无理数},
C={ x|x是实数};集合A、 B与集合C之间都具有这样一种关系:集合C是由集合A或集合B的元素组成的。一,并集一般地,由所有属于集合A或属于集合B的元素所
组成的集合,叫做A,B的并集.记作:A∪B(读作"A并B"),即A∪B={x|x∈A,或x∈B}.如:{1,2,3,6}∪{1,2,5,10}={1,2,3,5,6,10}.可用Venn图表示:ABBA集合A和B合并在一起得到的集合叫做集合A
和集合B的并(图中的阴影部分)BA1。 设A={4,5,6,8}, B={3,5,7,8},求A∪B.2。 设集合A={x|x为等腰三角形},集合B={x|x为直角三角形} 求A∪B.练习考察下列各个集合,你能说出集合A、 B与集合C之
间的关系吗?(1) A={2,4,6,8,10},B={3,5,8,12},C={8};(2) A={x|x是沂水四中在校的女生},
B={ x|x是沂水四中在校的高一学生}
C={ x|x是沂水四中在校的高一女生}集合A、 B与集合C之间都具有这样一种关系:集合C是有那些既属于集合A且属于集合B的所
有元素组成的二,交集一般地,由所有属于A且属于B的元素所组成的
集合,叫做A,B的交集.记作A∩B(读作"A交B"),即A∩B={x|x∈A,且x∈B}.如:{1,2,3,6}∩{1,2,5,10}={1,2}.
又如:A={a,b,c,d,e},B={c,d,e,f}.则A∩B={c,d,e}.可用Venn图表示:BABA如上图,集合A和B的公共部分叫做集合A和集合
B的交(图1的阴影部分)1。 新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学},
求A∩B.练习3. 交集的性质4.并集的性质例题分析2.设 ,
若 ,求实数m的取值范围。例题分析3.设集合 ,
且 ,求实数a的取值范围变式:设 ,
又 ,求实数a,b和c
的值。例题分析例题分析课堂小结并集
交集
交集、并集的性质
