18.2.3正方形巩固提升练习(含答案)2022-2023学年人教版八年级下册数学
文档属性
| 名称 | 18.2.3正方形巩固提升练习(含答案)2022-2023学年人教版八年级下册数学 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 00:00:00 | ||
图片预览




文档简介
18.2.3正方形 巩固提升练习
一、单选题
1.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是()
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
2.如图,正方形ABCD的边长为5,E是AD边上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线交AB于M,交CD于N.设运动时间为t秒,当PM∥BC时,t的值为( )
A. B.2 C. D.
3.如图,四边形 是边长为 的正方形,以对角线 为边作第二个正方形 ,连接 ,得到 ;再以对角线 为边作第三个正方形 ,连接 ,得到 ,再以对角线 为边作第四个正方形 ,连接 ,得到 ,设 ,的面积分别为 ,如此下去,则 的值为( )
A. B. C. D.1
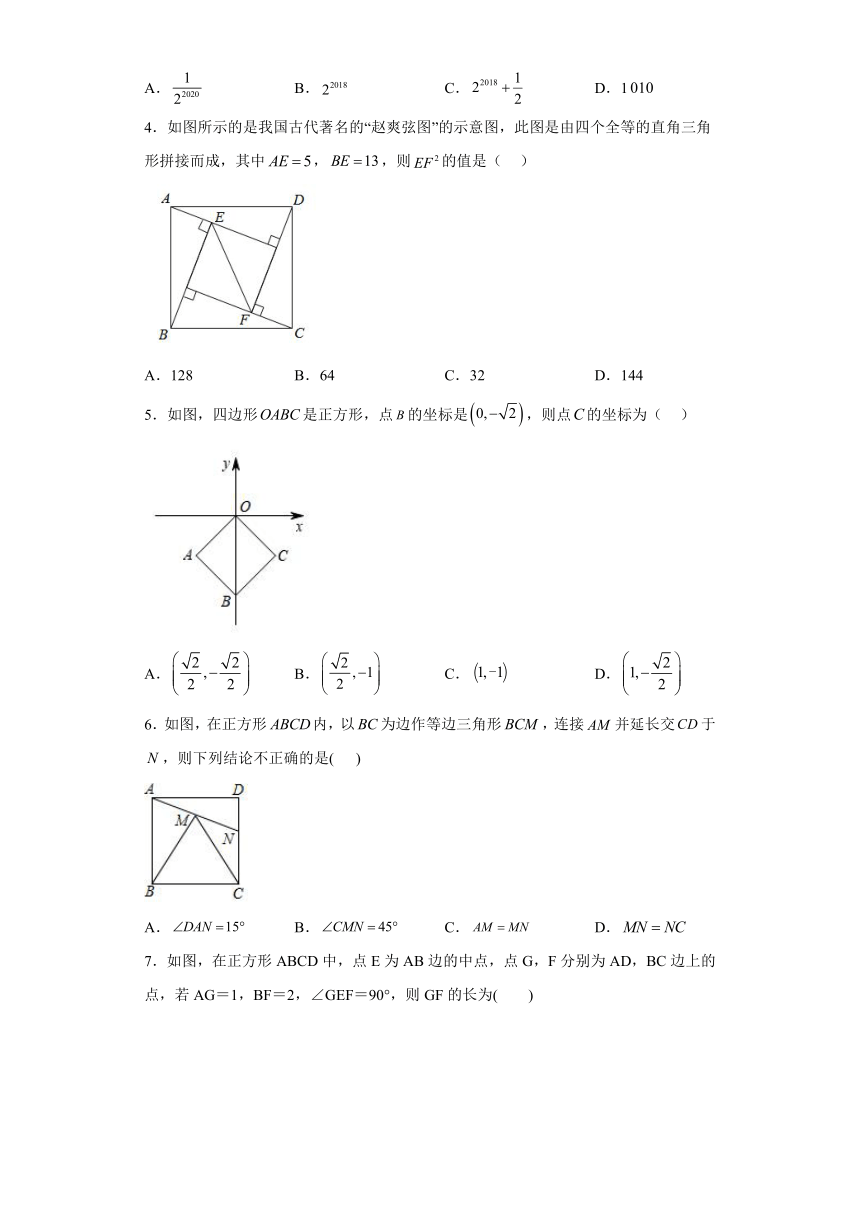
4.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.128 B.64 C.32 D.144
5.如图,四边形是正方形,点的坐标是,则点的坐标为( )
A. B. C. D.
6.如图,在正方形内,以为边作等边三角形,连接并延长交于,则下列结论不正确的是( )
A. B. C. D.
7.如图,在正方形ABCD中,点E为AB边的中点,点G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A.3 B.4 C.5 D.6
8.如图,正方形的面积为,点为边上一动点,点为边上一动点,连接、,点和点在运动的过程中始终保持,则的周长( )
A. B.8cm C.6cm D.4cm
9.如图,在正方形ABCD中,E,F分别是AB,BC的中点,CE,DF交于点G,连接AG.下列结论:①CE=DF;②CE⊥DF;③∠AGE=∠CDF;④∠EAG=30°.其中正确的结论是( )
A.①② B.①③ C.①②④ D.①②③
10.如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )
A.112.5° B.125° C.135° D.150°
二、填空题
11.如图,已知正方形的边长为,点是边的中点,点是对角线上的动点,则的最小值是_______.
12.如图,在正方形中.若以为底边向其形外作等腰直角,连接,则的长为______.
13.定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为________;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________.
14.如图,四边形ABCD是正方形,△ABE是等边三角形,EC=2-2,则正方形ABCD的面积为________.
15.如图,四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BAD,AC=7,AD=3,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度为_____.
三、解答题
16.如图 ,已知点 C 为线段 AB 上一点,四边形ACMF、BCNE 是两个正方形.求证:AN=BM
17.我们定义:只有一组对角相等的凸四边形叫做等对角四边形.
(1)四边形ABCD是等对角四边形,A≠C,若A=50°,B=100°,则C=_____,D=_____.
(2)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在格点上,按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.
(3)如图③,在平行四边形ABCD中,A=60°,AB=12,AD=6,点E为AB的中点,过点E作EFDC,交DC于点F.点P是射线FE上一个动点,设FP=x,求以点A、D、E、P为顶点的四边形为等对角四边形时x的值.
18.如图,在正方形中,,E为正方形内一点,,,连结,,过点D作,垂足为点F,交的延长线于点G,连结.
(1)当时,求的度数.
(2)判断的形状,并说明理由.
(3)当时,求的长.
19.在内画正方形,使顶点,在上,顶点,分别在,上.(不求写画法,但要保留画图痕迹)
20.问题探究
(1)如图①,在正方形中,,点为的中点,过点作于点,则的长为__________;
(2)如图②,四边形与四边形都是正方形,点、分别在、上,连接,求证:;
问题解决
(3)为打造宜居环境,建设美丽家园,计划对如图③所示的菱形空地进行绿化改造,菱形足够大,,是一条水渠,点、分别是、的中点,点、分别在、上,点在菱形内部,现将四边形改造成草地,并沿线段、、种植乔木绿化带,已知,,米,且种植乔木绿化带每米费用约为200元(不计宽度),请计算种植上述三条乔木绿化带大约需花多少钱?
参考答案
1.D
2.B
3.B
4.A
5.A
6.D
7.A
8.A
9.D
10.A
11.
12.
13. 12
14.8
15.5π
16.∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM, NC =BC,∠ACN=∠BCM=90°,
∴△ACN≌△MCB(SAS),
∴AN=BM.
17.(1)
∵四边形ABCD是等对角四边形,,
∴D=B=100°,
∴C=360°-A-B-D=360°-50°-100°-100°=110°.
故答案为:110°;100°.
(2)
由题意可得:等对角四边形ABCD如图所示
(3)
如图③,作DHAB于H,
∵在RtADH中,A=60°,
∴ADH=30°,
∴AH=AD=3,
∴DH=3,
∵点E为AB的中点,
∴AE=AB=6,
∴DF=HE=6-3=3,
如图③,当ADP=AEP=90°时,DPE=120°,
∴DPF=60°,
在含30°的RtDFP中,
FP=x=,
如图④,连接DE,
∵AD=AE=6,A=60°,
∴ADE为等边三角形,
当APE=ADE=60°,
在含30°的RtAEP中
EP=2,
∴x=EF+EP=.
综上所述x=或.
18.解:(1)四边形是正方形,
,,
,
,
,
,
.
(2)结论:是等腰直角三角形.
理由:,,
是的垂直平分线,
,
,
,
,,
,
,
,
,
,
为等腰直角三角形.
(3)如图,连接,
四边形是正方形,
,
为等腰直角三角形,,
,
,
,
,
(负值已舍去).
19.解:画法(不要求):在上任取一点,画与;
画正方形,使,在上;
画射线,与相交于;
画,与相交于;
画于,于.
四边形就是求作的正方形.
20.(1)解:是的中点,
是正方形的对角线
是等腰直角三角形
故答案为
(2)证明:过点作,交于,
∴,
在正方形与正方形中,,,,
∴,,
∴,,
∴,
∴.
∵,,
∴,
∴.
(3)解:在菱形中,,,
∵点、分别是、的中点,
∴,,
∴,
∴是等边三角形,
∴,
连接,过点作交于点,
∴,
∴是等边三角形,
∴,
由,,易得是等边三角形,
∴,,
∴,
∴.
∴,
∵种植每米乔木绿化带费用约为200元,
∴种植、、三条乔木绿化带大约需(元).
一、单选题
1.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是()
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
2.如图,正方形ABCD的边长为5,E是AD边上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线交AB于M,交CD于N.设运动时间为t秒,当PM∥BC时,t的值为( )
A. B.2 C. D.
3.如图,四边形 是边长为 的正方形,以对角线 为边作第二个正方形 ,连接 ,得到 ;再以对角线 为边作第三个正方形 ,连接 ,得到 ,再以对角线 为边作第四个正方形 ,连接 ,得到 ,设 ,的面积分别为 ,如此下去,则 的值为( )
A. B. C. D.1
4.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.128 B.64 C.32 D.144
5.如图,四边形是正方形,点的坐标是,则点的坐标为( )
A. B. C. D.
6.如图,在正方形内,以为边作等边三角形,连接并延长交于,则下列结论不正确的是( )
A. B. C. D.
7.如图,在正方形ABCD中,点E为AB边的中点,点G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A.3 B.4 C.5 D.6
8.如图,正方形的面积为,点为边上一动点,点为边上一动点,连接、,点和点在运动的过程中始终保持,则的周长( )
A. B.8cm C.6cm D.4cm
9.如图,在正方形ABCD中,E,F分别是AB,BC的中点,CE,DF交于点G,连接AG.下列结论:①CE=DF;②CE⊥DF;③∠AGE=∠CDF;④∠EAG=30°.其中正确的结论是( )
A.①② B.①③ C.①②④ D.①②③
10.如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )
A.112.5° B.125° C.135° D.150°
二、填空题
11.如图,已知正方形的边长为,点是边的中点,点是对角线上的动点,则的最小值是_______.
12.如图,在正方形中.若以为底边向其形外作等腰直角,连接,则的长为______.
13.定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为________;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________.
14.如图,四边形ABCD是正方形,△ABE是等边三角形,EC=2-2,则正方形ABCD的面积为________.
15.如图,四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BAD,AC=7,AD=3,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度为_____.
三、解答题
16.如图 ,已知点 C 为线段 AB 上一点,四边形ACMF、BCNE 是两个正方形.求证:AN=BM
17.我们定义:只有一组对角相等的凸四边形叫做等对角四边形.
(1)四边形ABCD是等对角四边形,A≠C,若A=50°,B=100°,则C=_____,D=_____.
(2)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在格点上,按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.
(3)如图③,在平行四边形ABCD中,A=60°,AB=12,AD=6,点E为AB的中点,过点E作EFDC,交DC于点F.点P是射线FE上一个动点,设FP=x,求以点A、D、E、P为顶点的四边形为等对角四边形时x的值.
18.如图,在正方形中,,E为正方形内一点,,,连结,,过点D作,垂足为点F,交的延长线于点G,连结.
(1)当时,求的度数.
(2)判断的形状,并说明理由.
(3)当时,求的长.
19.在内画正方形,使顶点,在上,顶点,分别在,上.(不求写画法,但要保留画图痕迹)
20.问题探究
(1)如图①,在正方形中,,点为的中点,过点作于点,则的长为__________;
(2)如图②,四边形与四边形都是正方形,点、分别在、上,连接,求证:;
问题解决
(3)为打造宜居环境,建设美丽家园,计划对如图③所示的菱形空地进行绿化改造,菱形足够大,,是一条水渠,点、分别是、的中点,点、分别在、上,点在菱形内部,现将四边形改造成草地,并沿线段、、种植乔木绿化带,已知,,米,且种植乔木绿化带每米费用约为200元(不计宽度),请计算种植上述三条乔木绿化带大约需花多少钱?
参考答案
1.D
2.B
3.B
4.A
5.A
6.D
7.A
8.A
9.D
10.A
11.
12.
13. 12
14.8
15.5π
16.∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM, NC =BC,∠ACN=∠BCM=90°,
∴△ACN≌△MCB(SAS),
∴AN=BM.
17.(1)
∵四边形ABCD是等对角四边形,,
∴D=B=100°,
∴C=360°-A-B-D=360°-50°-100°-100°=110°.
故答案为:110°;100°.
(2)
由题意可得:等对角四边形ABCD如图所示
(3)
如图③,作DHAB于H,
∵在RtADH中,A=60°,
∴ADH=30°,
∴AH=AD=3,
∴DH=3,
∵点E为AB的中点,
∴AE=AB=6,
∴DF=HE=6-3=3,
如图③,当ADP=AEP=90°时,DPE=120°,
∴DPF=60°,
在含30°的RtDFP中,
FP=x=,
如图④,连接DE,
∵AD=AE=6,A=60°,
∴ADE为等边三角形,
当APE=ADE=60°,
在含30°的RtAEP中
EP=2,
∴x=EF+EP=.
综上所述x=或.
18.解:(1)四边形是正方形,
,,
,
,
,
,
.
(2)结论:是等腰直角三角形.
理由:,,
是的垂直平分线,
,
,
,
,,
,
,
,
,
,
为等腰直角三角形.
(3)如图,连接,
四边形是正方形,
,
为等腰直角三角形,,
,
,
,
,
(负值已舍去).
19.解:画法(不要求):在上任取一点,画与;
画正方形,使,在上;
画射线,与相交于;
画,与相交于;
画于,于.
四边形就是求作的正方形.
20.(1)解:是的中点,
是正方形的对角线
是等腰直角三角形
故答案为
(2)证明:过点作,交于,
∴,
在正方形与正方形中,,,,
∴,,
∴,,
∴,
∴.
∵,,
∴,
∴.
(3)解:在菱形中,,,
∵点、分别是、的中点,
∴,,
∴,
∴是等边三角形,
∴,
连接,过点作交于点,
∴,
∴是等边三角形,
∴,
由,,易得是等边三角形,
∴,,
∴,
∴.
∴,
∵种植每米乔木绿化带费用约为200元,
∴种植、、三条乔木绿化带大约需(元).
