人教版数学八年级下册19.2.2 一次函数 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册19.2.2 一次函数 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 00:00:00 | ||
图片预览

文档简介
19.2.2 一次函数 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列一次函数中,y随x增大而增大的有( )
①;②;③;④;⑤.
A.①②③ B.①②⑤ C.①③⑤ D.①④⑤
2.一次函数的图象经过( )
A.第一、二、三象限 B.第二、三、四象限 C.第一、二、四象限 D.第一、三、四象限
3.若一次函数的图像经过点,且函数值随着增大而减小,则点的坐标可能为( )
A. B. C. D.
4.已知函数,是的一次函数,则的值是( )
A.1 B. C.1或 D.任意实数
5.直线y= 2x+5上有三个点( 2,y1) ,( 1,y2) ,(1,y3),则y1,y2,y3的大小关系是( )
A. B. C. D.
6.将直线向下平移2个单位长度,所得直线的表达式为( )
A. B. C. D.
7.若点A(x1,y1)和B(x2,y2) 都在一次函数y=(k)x+2(k为常数)的图像上,且当x1y2,则k的值可能是( )
A.k=0 B.k=1 C.k=2 D.k=3
8.已知一次函数y=mnx与y=mx+n(m,n为常数,且mn≠0),则它们在同一平面直角坐标系内的图象可能为( )
A.B.C.D.
9.如图,点A,B,C在一次函数的图象上,它们的横坐标依次为,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积和是( )
A.1 B.3 C. D.
10.如图,直线与的交点的横坐标为,则关于的不等式的整数解为( ).
A. B.
C. D.
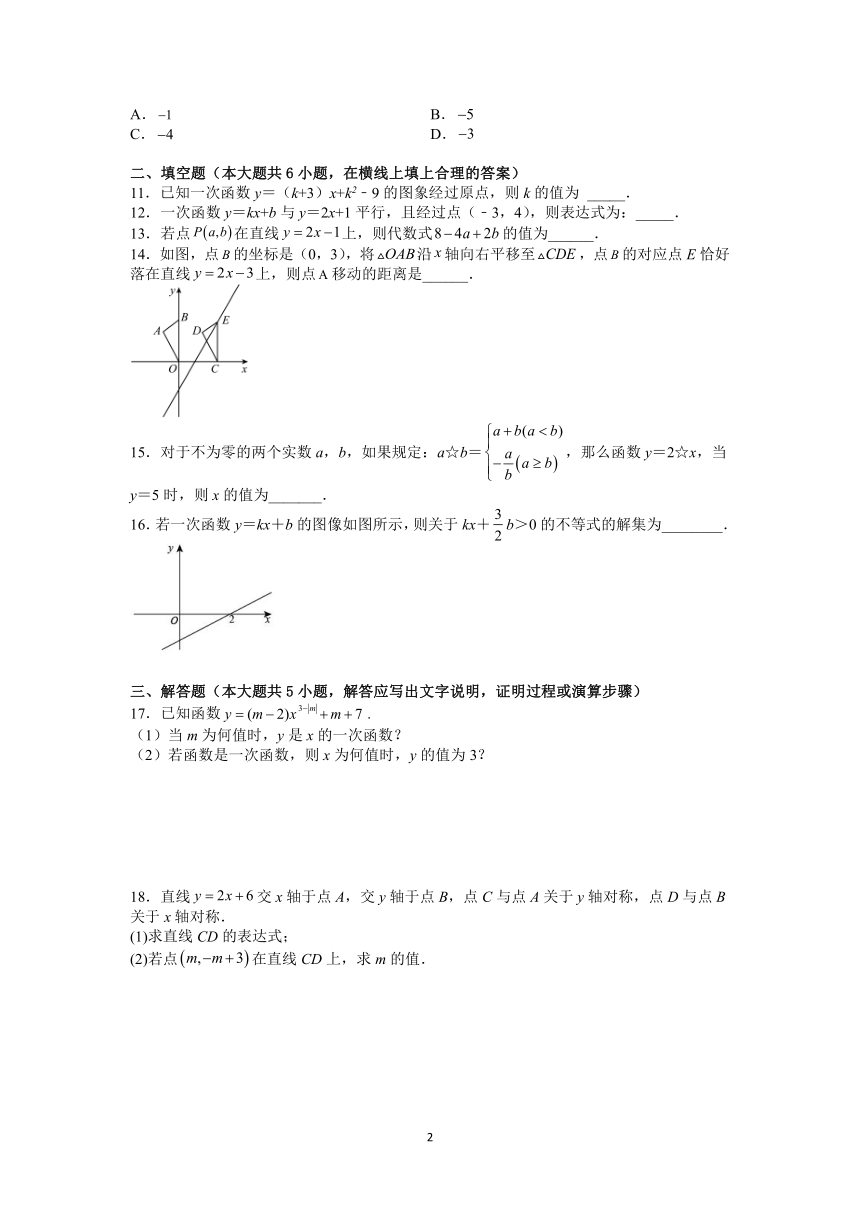
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知一次函数y=(k+3)x+k2﹣9的图象经过原点,则k的值为 _____.
12.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
13.若点在直线上,则代数式的值为______.
14.如图,点的坐标是(0,3),将沿轴向右平移至,点的对应点E恰好落在直线上,则点移动的距离是______.
15.对于不为零的两个实数a,b,如果规定:a☆b=,那么函数y=2☆x,当y=5时,则x的值为_______.
16.若一次函数y=kx+b的图像如图所示,则关于kx+b>0的不等式的解集为________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.已知函数.
(1)当m为何值时,y是x的一次函数?
(2)若函数是一次函数,则x为何值时,y的值为3?
18.直线交x轴于点A,交y轴于点B,点C与点A关于y轴对称,点D与点B关于x轴对称.
(1)求直线CD的表达式;
(2)若点在直线CD上,求m的值.
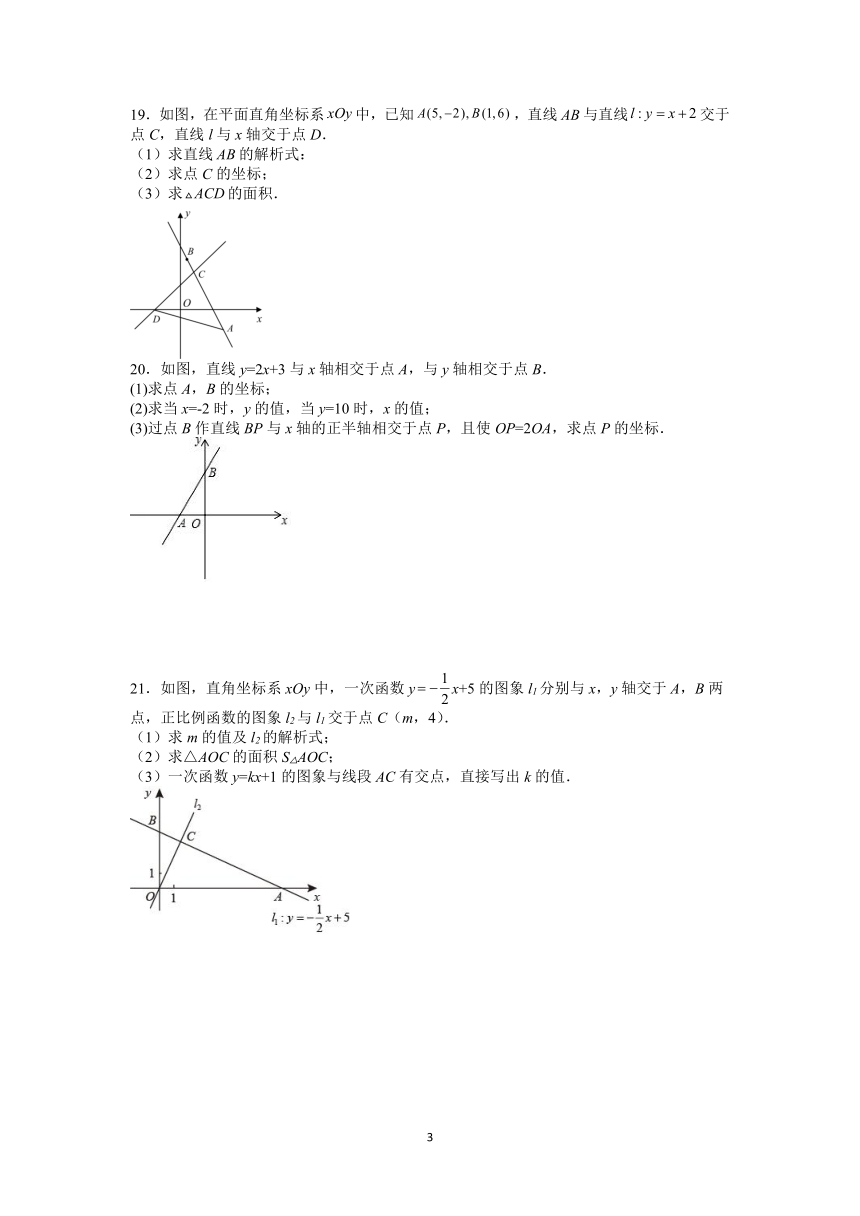
19.如图,在平面直角坐标系中,已知,直线与直线交于点C,直线l与x轴交于点D.
(1)求直线的解析式:
(2)求点C的坐标;
(3)求的面积.
20.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴的正半轴相交于点P,且使OP=2OA,求点P的坐标.
21.如图,直角坐标系xOy中,一次函数yx+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求△AOC的面积S△AOC;
(3)一次函数y=kx+1的图象与线段AC有交点,直接写出k的值.
答案:
1.C 2.A 3.D 4.A 5.C 6.A 7.A 8.D 9.B 10.D 11.3
12.y=2x+10 13.6 14.3 15.3或- 16.
17.(1)由是一次函数得,
解得.
故当时,是一次函数.
(2)由(1)可知.
当时,,解得.
故当时,y的值为3.
18.(1)解:把代入,得,解得,
∴,
当时,,
∴,
∵点C与点A关于y轴对称,点D与点B关于x轴对称,
∴,,
设直线CD的表达式为,根据题意,得,,
将代入,得,
∴直线CD的函数表达式为;
(2)解:将代入
得:,
解得.
∴m的值为3.
19.解:(1)设直线AB的解析式为:y=kx+b,
将A(5,-2),B(1,6)代入,
得:,解得:,
∴直线AB的解析式为:y=-2x+8;
(2)∵直线与直线y=x+2交于点C,
则令-2x+8=x+2,
解得:x=2,代入y=x+2,得y=4,
∴C(2,4);
(3)∵直线l与x轴交于点D,
∴在y=x+2中,令y=0,则x=-2,
∴D(-2,0),设E为直线AB与x轴交点,
在y=-2x+8中,令y=0,则x=4,
∴E(4,0),
∴△ACD的面积=△CDE的面积+△ADE的面积==.
20.(1)对于y=2x+3,令x=0,得:y=3,
∴B(0,3).
令y=0,得:2x+3=0,
解得,
∴A(,0);
(2)
当x=-2时,y=2×(-2)+3=-1;
当y=10时,则2x+3=10,
解得;
(3)
∵A(,0),
∴OA=.
∵OP=2OA,
∴OP=3.
∵点P在x轴的正半轴,
∴点P的坐标为(3,0).
21.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得:4=﹣m+5,解得:m=2
∴C(2,4),
设l2的解析式为y=ax,则有4=2a,解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,则CD=4,
由点A、B在一次函数y=﹣x+5上,
令y=0,则x=0,x=10,
∴O(0,0),A(10,0)
∴AO=10
∴S△AOC=×10×4=20;
(3)当y=kx+1恰好经过点C时,有4=2k+1,解得:k=
当y=kx+1恰好经过点A时,有0=10k+1,解得:k=
所以当时,一次函数y=kx+1的图象与线段AC有交点.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列一次函数中,y随x增大而增大的有( )
①;②;③;④;⑤.
A.①②③ B.①②⑤ C.①③⑤ D.①④⑤
2.一次函数的图象经过( )
A.第一、二、三象限 B.第二、三、四象限 C.第一、二、四象限 D.第一、三、四象限
3.若一次函数的图像经过点,且函数值随着增大而减小,则点的坐标可能为( )
A. B. C. D.
4.已知函数,是的一次函数,则的值是( )
A.1 B. C.1或 D.任意实数
5.直线y= 2x+5上有三个点( 2,y1) ,( 1,y2) ,(1,y3),则y1,y2,y3的大小关系是( )
A. B. C. D.
6.将直线向下平移2个单位长度,所得直线的表达式为( )
A. B. C. D.
7.若点A(x1,y1)和B(x2,y2) 都在一次函数y=(k)x+2(k为常数)的图像上,且当x1
A.k=0 B.k=1 C.k=2 D.k=3
8.已知一次函数y=mnx与y=mx+n(m,n为常数,且mn≠0),则它们在同一平面直角坐标系内的图象可能为( )
A.B.C.D.
9.如图,点A,B,C在一次函数的图象上,它们的横坐标依次为,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积和是( )
A.1 B.3 C. D.
10.如图,直线与的交点的横坐标为,则关于的不等式的整数解为( ).
A. B.
C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知一次函数y=(k+3)x+k2﹣9的图象经过原点,则k的值为 _____.
12.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
13.若点在直线上,则代数式的值为______.
14.如图,点的坐标是(0,3),将沿轴向右平移至,点的对应点E恰好落在直线上,则点移动的距离是______.
15.对于不为零的两个实数a,b,如果规定:a☆b=,那么函数y=2☆x,当y=5时,则x的值为_______.
16.若一次函数y=kx+b的图像如图所示,则关于kx+b>0的不等式的解集为________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.已知函数.
(1)当m为何值时,y是x的一次函数?
(2)若函数是一次函数,则x为何值时,y的值为3?
18.直线交x轴于点A,交y轴于点B,点C与点A关于y轴对称,点D与点B关于x轴对称.
(1)求直线CD的表达式;
(2)若点在直线CD上,求m的值.
19.如图,在平面直角坐标系中,已知,直线与直线交于点C,直线l与x轴交于点D.
(1)求直线的解析式:
(2)求点C的坐标;
(3)求的面积.
20.如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)求当x=-2时,y的值,当y=10时,x的值;
(3)过点B作直线BP与x轴的正半轴相交于点P,且使OP=2OA,求点P的坐标.
21.如图,直角坐标系xOy中,一次函数yx+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求△AOC的面积S△AOC;
(3)一次函数y=kx+1的图象与线段AC有交点,直接写出k的值.
答案:
1.C 2.A 3.D 4.A 5.C 6.A 7.A 8.D 9.B 10.D 11.3
12.y=2x+10 13.6 14.3 15.3或- 16.
17.(1)由是一次函数得,
解得.
故当时,是一次函数.
(2)由(1)可知.
当时,,解得.
故当时,y的值为3.
18.(1)解:把代入,得,解得,
∴,
当时,,
∴,
∵点C与点A关于y轴对称,点D与点B关于x轴对称,
∴,,
设直线CD的表达式为,根据题意,得,,
将代入,得,
∴直线CD的函数表达式为;
(2)解:将代入
得:,
解得.
∴m的值为3.
19.解:(1)设直线AB的解析式为:y=kx+b,
将A(5,-2),B(1,6)代入,
得:,解得:,
∴直线AB的解析式为:y=-2x+8;
(2)∵直线与直线y=x+2交于点C,
则令-2x+8=x+2,
解得:x=2,代入y=x+2,得y=4,
∴C(2,4);
(3)∵直线l与x轴交于点D,
∴在y=x+2中,令y=0,则x=-2,
∴D(-2,0),设E为直线AB与x轴交点,
在y=-2x+8中,令y=0,则x=4,
∴E(4,0),
∴△ACD的面积=△CDE的面积+△ADE的面积==.
20.(1)对于y=2x+3,令x=0,得:y=3,
∴B(0,3).
令y=0,得:2x+3=0,
解得,
∴A(,0);
(2)
当x=-2时,y=2×(-2)+3=-1;
当y=10时,则2x+3=10,
解得;
(3)
∵A(,0),
∴OA=.
∵OP=2OA,
∴OP=3.
∵点P在x轴的正半轴,
∴点P的坐标为(3,0).
21.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得:4=﹣m+5,解得:m=2
∴C(2,4),
设l2的解析式为y=ax,则有4=2a,解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,则CD=4,
由点A、B在一次函数y=﹣x+5上,
令y=0,则x=0,x=10,
∴O(0,0),A(10,0)
∴AO=10
∴S△AOC=×10×4=20;
(3)当y=kx+1恰好经过点C时,有4=2k+1,解得:k=
当y=kx+1恰好经过点A时,有0=10k+1,解得:k=
所以当时,一次函数y=kx+1的图象与线段AC有交点.
