9.2.1多边形的内角和 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
9.2.1多边形的内角和 教学设计
课题 9.2.1多边形的内角和 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 了解多边形的概念,掌握多边形的内角和公式。会用多边形的内角和进行简单的运算。从三角形的内角和入手,在熟悉和掌握多边形内角和定理的基础上,推理并掌握多边形的外角和定理.
核心素养分析 通过经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,体会数学的转化思想。体验数学活动充满着探索性和创造性,培养学生对学习数学勇于创新的精神.
学习目标 1.理解多边形和正多边形的定义.2.掌握多边形内角和公式.3.会用多边形内角和公式进行相关计算.
重点 探索和应用多边形内角和定理.
难点 推导多边形的内角和定理.
教学过程
教学环节 教师活动 学生活动 设计意图
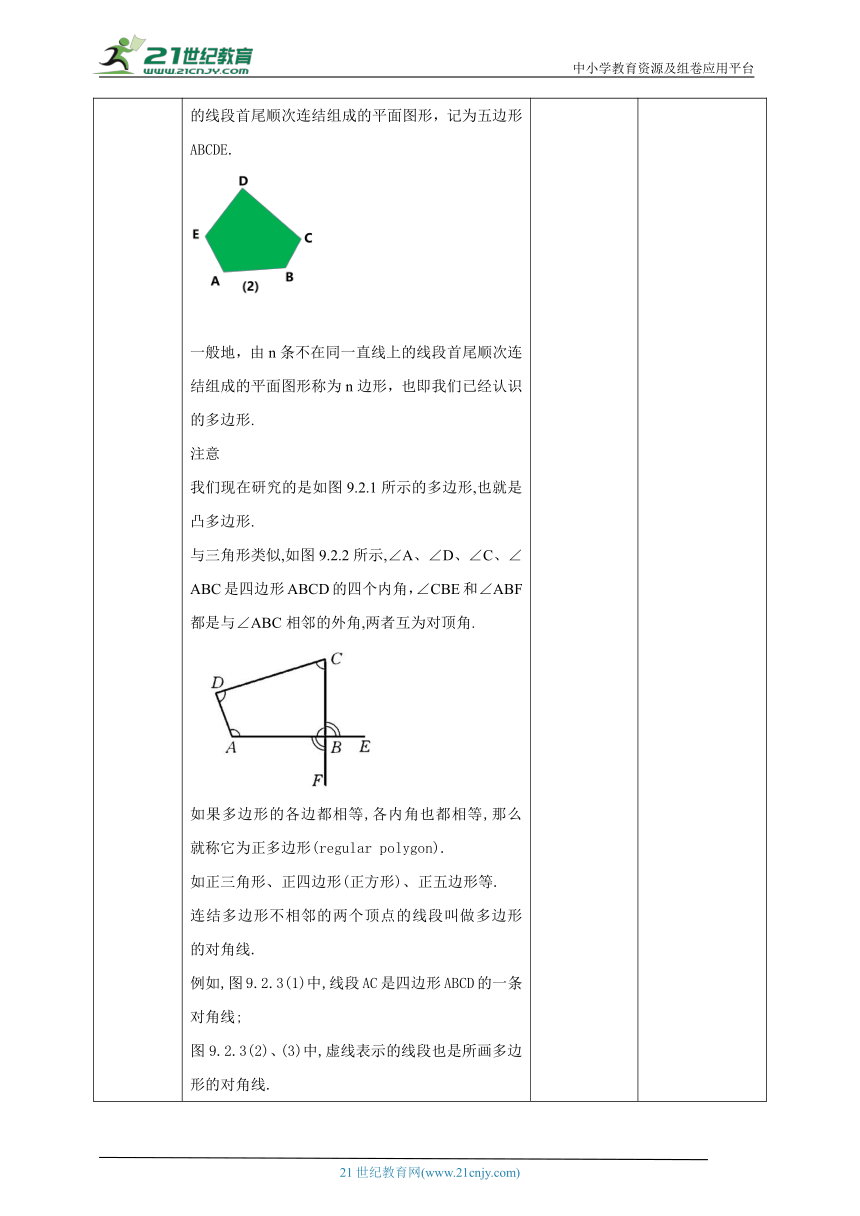
导入新课 一、创设情景,引出课题试一试三角形有三个内角、三条边,我们也可以把三角形称为三边形(但我们习惯称为三角形).我们已经知道什么叫三角形,你能说出什么叫四边形、五边形吗?图9.2.1(1)是四边形,它是由四条不在同一条直线上的线段首尾顺次连结组成的平面图形,记为四边形ABCD;图9.2.1(2)是五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形,记为五边形ABCDE.一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们已经认识的多边形.注意我们现在研究的是如图9.2.1所示的多边形,也就是凸多边形.与三角形类似,如图9.2.2所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角.如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形(regular polygon).如正三角形、正四边形(正方形)、正五边形等.连结多边形不相邻的两个顶点的线段叫做多边形的对角线.例如,图9.2.3(1)中,线段AC是四边形ABCD的一条对角线;图9.2.3(2)、(3)中,虚线表示的线段也是所画多边形的对角线. 思考自议学生自己去总结多边形的内角和,与学生讨论,教师进行归纳总结. 总结多边形的内角和的规律,引入新课,激发学生探究知识的欲望.
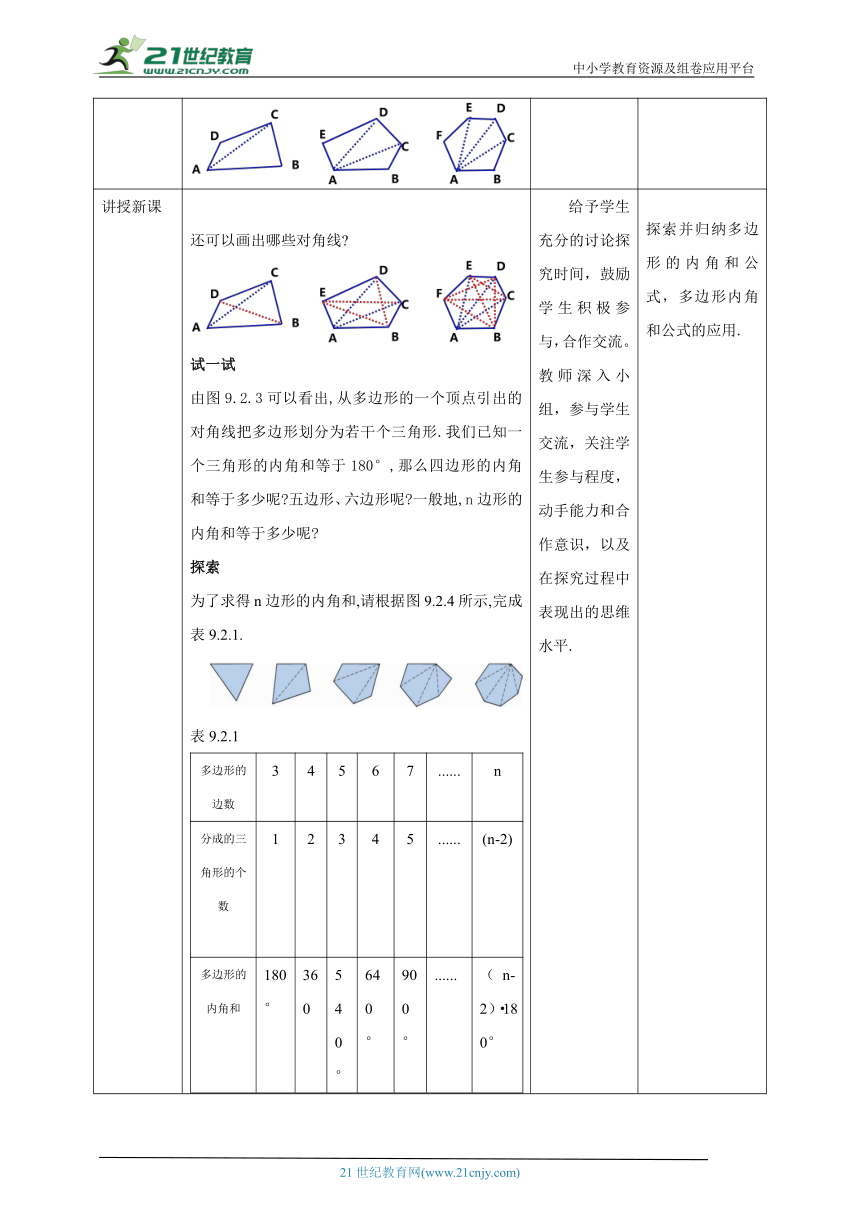
讲授新课 还可以画出哪些对角线 试一试由图9.2.3可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形.我们已知一个三角形的内角和等于180°,那么四边形的内角和等于多少呢 五边形、六边形呢 一般地,n边形的内角和等于多少呢 探索为了求得n边形的内角和,请根据图9.2.4所示,完成表9.2.1.表9.2.1多边形的边数34567......n分成的三角形的个数12345......(n-2)多边形的内角和180°360540°640°900°......(n-2)·180°由此,我们得出n边形的内角和为(n -2) ·1800.二、提炼概念n边形的内角和为(n -2) ·1800.三、典例精讲例1:一个多边形的内角和等于2160°,它是几边形?解:设这个多边形的边数为n,则(n-2 )×180°= 2160°, 解得n = 14. 所以这是一个十四边形.例2:已知一个正十边形.(1)求这个正十边形的内角和;(2)要使这个多边形的内角和增加1080°,那么还要增加几条边?解:(1)(10-2)×180°=1440°. (2)若内角和增加1080°,则新多边形的内角和为1440°+1080°=2520°,新多边形的边数为2520°÷180°+2=16.即还要增加6条边. 给予学生充分的讨论探究时间,鼓励学生积极参与,合作交流。教师深入小组,参与学生交流,关注学生参与程度,动手能力和合作意识,以及在探究过程中表现出的思维水平. 探索并归纳多边形的内角和公式,多边形内角和公式的应用.
课堂练习 四、巩固训练1、已知一个正多边形的一个内角为150度,则它的边数为( ) A. 12 B. 8 C. 9 D. 7 A2.下列说法中,正确的有( )(1)三角形是边数最少的多边形;(2)由n条线段连结起来组成的图形叫做多边形;(3)n边形有n条边、n个顶点、2n个内角和外角;A.1个 B.2个 C.3个 D.4个 A3.把一张形状是多边形的纸片剪去其中一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )A. 六边形 B . 五边形 C.四边形 D.三角形 A4. 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.解:∵1800÷180=10,∴原多边形边数为10+2=12.∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,∴新多边形的边数可能是11,12,13,∴新多边形的内角和可能是1620°,1800°,1980°.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
9.2.1多边形的内角和 教学设计
课题 9.2.1多边形的内角和 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 了解多边形的概念,掌握多边形的内角和公式。会用多边形的内角和进行简单的运算。从三角形的内角和入手,在熟悉和掌握多边形内角和定理的基础上,推理并掌握多边形的外角和定理.
核心素养分析 通过经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,体会数学的转化思想。体验数学活动充满着探索性和创造性,培养学生对学习数学勇于创新的精神.
学习目标 1.理解多边形和正多边形的定义.2.掌握多边形内角和公式.3.会用多边形内角和公式进行相关计算.
重点 探索和应用多边形内角和定理.
难点 推导多边形的内角和定理.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题试一试三角形有三个内角、三条边,我们也可以把三角形称为三边形(但我们习惯称为三角形).我们已经知道什么叫三角形,你能说出什么叫四边形、五边形吗?图9.2.1(1)是四边形,它是由四条不在同一条直线上的线段首尾顺次连结组成的平面图形,记为四边形ABCD;图9.2.1(2)是五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形,记为五边形ABCDE.一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们已经认识的多边形.注意我们现在研究的是如图9.2.1所示的多边形,也就是凸多边形.与三角形类似,如图9.2.2所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角.如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形(regular polygon).如正三角形、正四边形(正方形)、正五边形等.连结多边形不相邻的两个顶点的线段叫做多边形的对角线.例如,图9.2.3(1)中,线段AC是四边形ABCD的一条对角线;图9.2.3(2)、(3)中,虚线表示的线段也是所画多边形的对角线. 思考自议学生自己去总结多边形的内角和,与学生讨论,教师进行归纳总结. 总结多边形的内角和的规律,引入新课,激发学生探究知识的欲望.
讲授新课 还可以画出哪些对角线 试一试由图9.2.3可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形.我们已知一个三角形的内角和等于180°,那么四边形的内角和等于多少呢 五边形、六边形呢 一般地,n边形的内角和等于多少呢 探索为了求得n边形的内角和,请根据图9.2.4所示,完成表9.2.1.表9.2.1多边形的边数34567......n分成的三角形的个数12345......(n-2)多边形的内角和180°360540°640°900°......(n-2)·180°由此,我们得出n边形的内角和为(n -2) ·1800.二、提炼概念n边形的内角和为(n -2) ·1800.三、典例精讲例1:一个多边形的内角和等于2160°,它是几边形?解:设这个多边形的边数为n,则(n-2 )×180°= 2160°, 解得n = 14. 所以这是一个十四边形.例2:已知一个正十边形.(1)求这个正十边形的内角和;(2)要使这个多边形的内角和增加1080°,那么还要增加几条边?解:(1)(10-2)×180°=1440°. (2)若内角和增加1080°,则新多边形的内角和为1440°+1080°=2520°,新多边形的边数为2520°÷180°+2=16.即还要增加6条边. 给予学生充分的讨论探究时间,鼓励学生积极参与,合作交流。教师深入小组,参与学生交流,关注学生参与程度,动手能力和合作意识,以及在探究过程中表现出的思维水平. 探索并归纳多边形的内角和公式,多边形内角和公式的应用.
课堂练习 四、巩固训练1、已知一个正多边形的一个内角为150度,则它的边数为( ) A. 12 B. 8 C. 9 D. 7 A2.下列说法中,正确的有( )(1)三角形是边数最少的多边形;(2)由n条线段连结起来组成的图形叫做多边形;(3)n边形有n条边、n个顶点、2n个内角和外角;A.1个 B.2个 C.3个 D.4个 A3.把一张形状是多边形的纸片剪去其中一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )A. 六边形 B . 五边形 C.四边形 D.三角形 A4. 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.解:∵1800÷180=10,∴原多边形边数为10+2=12.∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,∴新多边形的边数可能是11,12,13,∴新多边形的内角和可能是1620°,1800°,1980°.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
