[重点校]河南师大附中2013-2014学年高中数学选修4-1:24弦切角的性质 学案
文档属性
| 名称 | [重点校]河南师大附中2013-2014学年高中数学选修4-1:24弦切角的性质 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 76.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-30 21:17:33 | ||
图片预览

文档简介
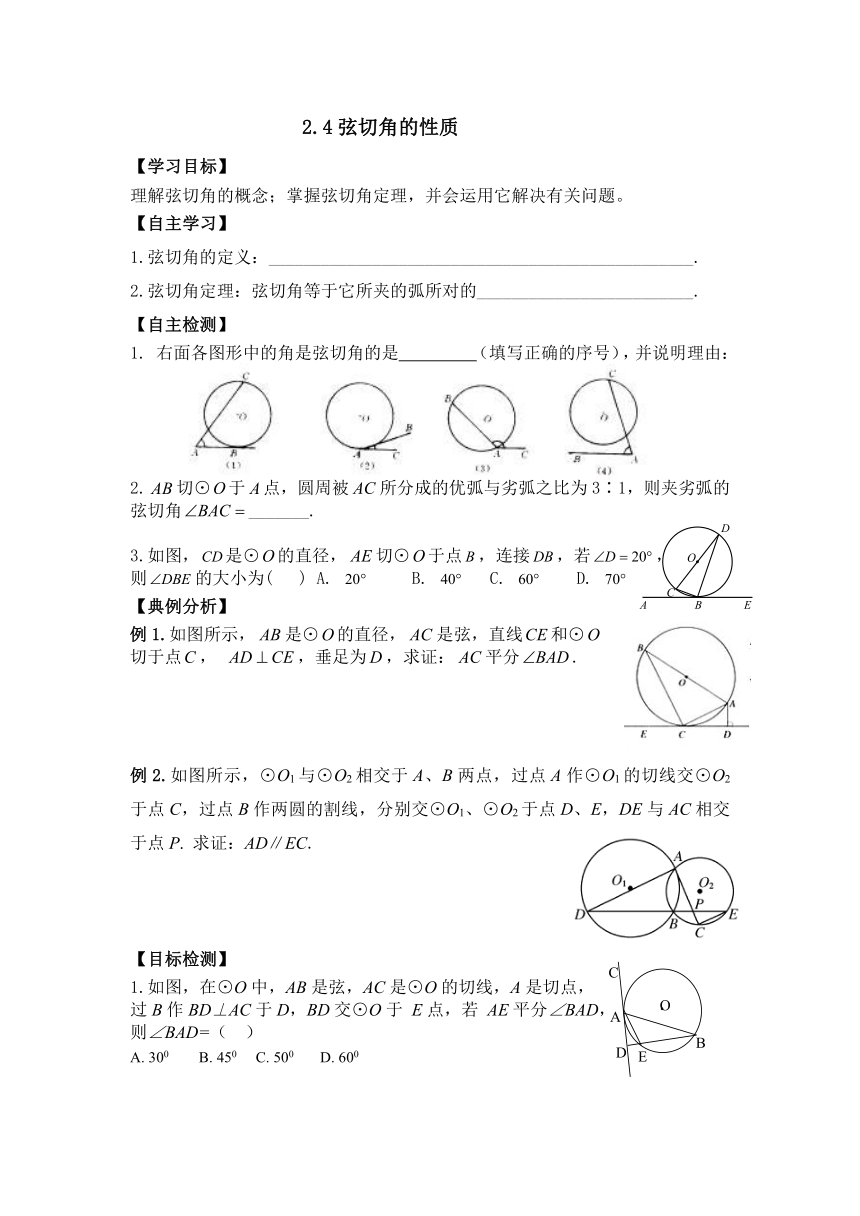
2.4弦切角的性质
【学习目标】
理解弦切角的概念;掌握弦切角定理,并会运用它解决有关问题。
【自主学习】
1.弦切角的定义:_________________________________________________.
2.弦切角定理:弦切角等于它所夹的弧所对的_________________________.
【自主检测】
右面各图形中的角是弦切角的是 (填写正确的序号),并说明理由:
2.切⊙于点,圆周被所分成的优弧与劣弧之比为3∶1,则夹劣弧的弦切角_______.
3.如图,是⊙的直径,切⊙于点,连接,若,
则的大小为( ) A. B. C. D.
【典例分析】
例1.如图所示,是⊙的直径,是弦,直线和⊙
切于点, ,垂足为,求证:平分.
例2.如图所示,⊙O1与⊙O2相交于A、 ( http: / / www.21cnjy.com )B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P. 求证:AD∥EC.
【目标检测】
1.如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,
过B作BD⊥AC于D,BD交⊙O于 E点,若 AE平分∠BAD,
则∠BAD=( )
A. 300 B. 450 C. 500 D. 600
如图所示,AB是直径,点D在AB的延长线上,BD=OB,若CD切⊙O于C点,试分别求∠CAB、∠DCB、∠ECA的度数.
3.如图所示,△ABC内接于⊙O,点D在OC的延长线上,.
求证:AD是⊙O的切线.
4. 如图所示,圆上的弧,过C点的圆的切线与BA的延长线交于E点,证明:(1)∠ACE=∠BCD;(2)
【总结提升】弦切角与圆周角是很重要的与圆相 ( http: / / www.21cnjy.com )关的角.其主要功能在于协调与圆相关的各种角(如圆心角 圆周角等),是架设圆与三角形全等 三角形相似 与圆相关的各种直线(如弦 割线 切线)位置关系的桥梁.
C
B
D
E
O
A
C
E
O
A
B
D
【学习目标】
理解弦切角的概念;掌握弦切角定理,并会运用它解决有关问题。
【自主学习】
1.弦切角的定义:_________________________________________________.
2.弦切角定理:弦切角等于它所夹的弧所对的_________________________.
【自主检测】
右面各图形中的角是弦切角的是 (填写正确的序号),并说明理由:
2.切⊙于点,圆周被所分成的优弧与劣弧之比为3∶1,则夹劣弧的弦切角_______.
3.如图,是⊙的直径,切⊙于点,连接,若,
则的大小为( ) A. B. C. D.
【典例分析】
例1.如图所示,是⊙的直径,是弦,直线和⊙
切于点, ,垂足为,求证:平分.
例2.如图所示,⊙O1与⊙O2相交于A、 ( http: / / www.21cnjy.com )B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P. 求证:AD∥EC.
【目标检测】
1.如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,
过B作BD⊥AC于D,BD交⊙O于 E点,若 AE平分∠BAD,
则∠BAD=( )
A. 300 B. 450 C. 500 D. 600
如图所示,AB是直径,点D在AB的延长线上,BD=OB,若CD切⊙O于C点,试分别求∠CAB、∠DCB、∠ECA的度数.
3.如图所示,△ABC内接于⊙O,点D在OC的延长线上,.
求证:AD是⊙O的切线.
4. 如图所示,圆上的弧,过C点的圆的切线与BA的延长线交于E点,证明:(1)∠ACE=∠BCD;(2)
【总结提升】弦切角与圆周角是很重要的与圆相 ( http: / / www.21cnjy.com )关的角.其主要功能在于协调与圆相关的各种角(如圆心角 圆周角等),是架设圆与三角形全等 三角形相似 与圆相关的各种直线(如弦 割线 切线)位置关系的桥梁.
C
B
D
E
O
A
C
E
O
A
B
D
