同底数幂的乘法[上学期]
图片预览







文档简介
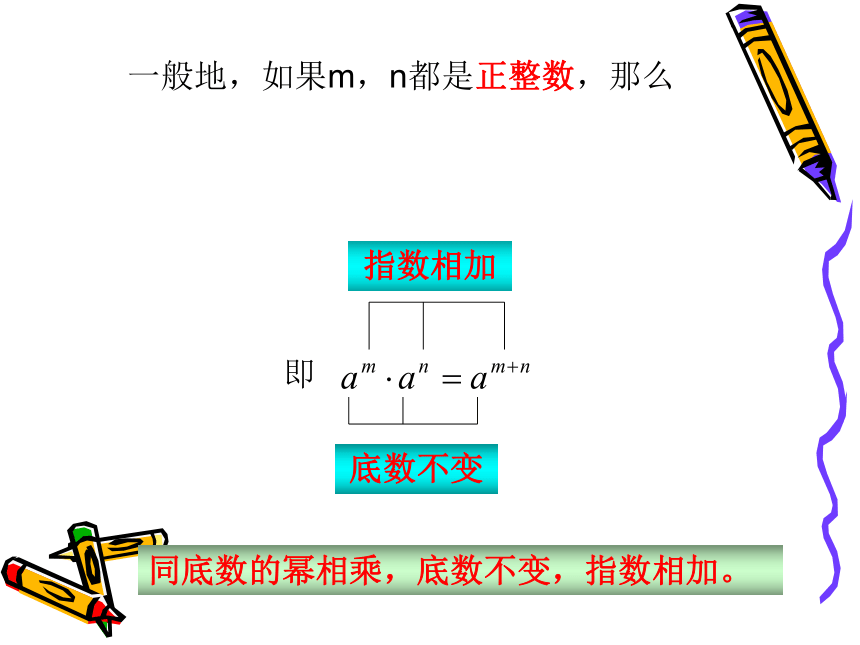
课件24张PPT。5.1同底数幂的乘法练市一中复习指数幂底数复习1.什么叫乘方?2.读出下表各式,说明底数和指数,并用乘法式子来表示。-22aa+12425求几个相同因数的积的运算叫做乘方。计算:103 × 102=(10 ×10 ×10) ×(10 ×10 ) ( )=10 ×10 ×10 ×10 ×10 ( )103 ×102解:根据幂的意义根据乘法结合律=105 ( )根据幂的意义即:103 × 102 = 1053+2=5计算:3+4=7幂的意义乘法结合律(根据 。)根据( 。)根据( 。)幂的意义=105+8幂的意义乘法结合律(根据 。)根据( 。)(根据 。)幂的意义一般地,如果m,n都是正整数,那么即同底数的幂相乘,底数不变,指数相加。下面的计算对不 对?如果不对,应怎样改正?⑴⑶⑸⑷⑵(二)补充练习:判断(正确的 打“√”,错误的打“×”) x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (3)x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5= -x5 ( )
(6)a2·a3- a3·a2 = 0 ( )
(7)x3·y5=(xy)8 ( ) (8) x7+x7=x14 ( )
√√××××××例1 计算:⑴108 ×103;⑶76 ×74;例2 化简:⑴(-2)8 ×(-2)7;⑵⑶想一想am · an · ap 等于什么?例2。我国自行研制的神威一号计算机的峰值运算速度达到每秒3840亿次,如果按这个速度工作一天,那么它能运算多少次(结果保留3 个有效数字)?解:3840亿次=3.84 × 103 ×10824小时=24 ×3.6 × 103(3.84 × 103 × 108 ) × (24 ×3.6 × 103 )
=
=
=( 3.84 × 24 ×3.6 ) × ( 103 × 108 × 103 )
331 . 776 × 10143 . 32 × 1016(次)答:它一天约能运算3 . 32 × 1016次同底数幂的乘法性质:底数 ,指数 .不变相加幂的意义:小 结做一做1、计算下列各式:
(1)102×103
(2)105×108
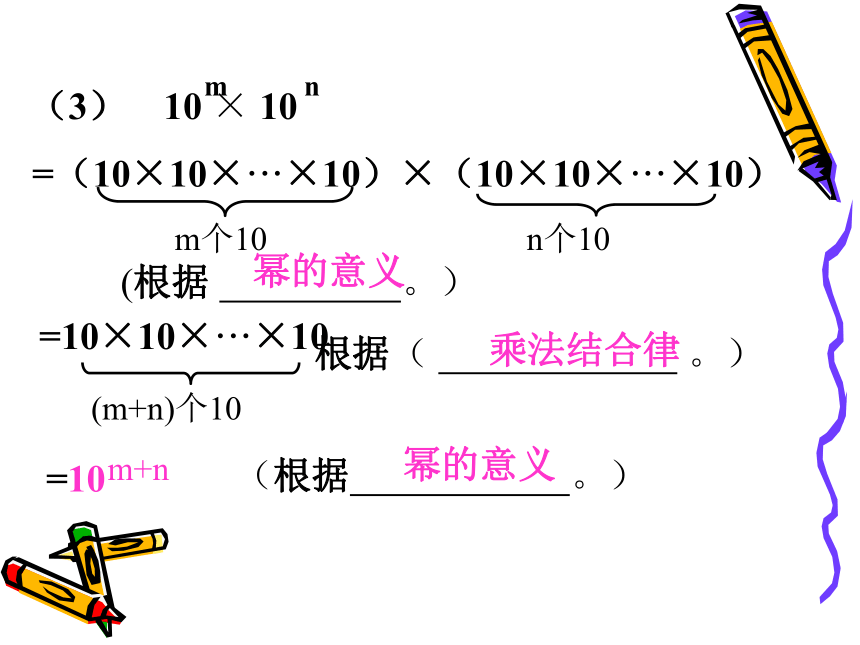
(3)10m×10n(m,n都是正整数).你发现了什么? 2. 2m×2n等于什么?(1/7)m×(1/7)n 呢?
(m,n 都是正整数)=2m+n=(2×2×···×2)×(2×2×···×2) m个2 n个22m×2n2、 (1/7)m ×(1/7)n= (1/7)m+n方法1 am·an·ap
=(am·an)·ap=am+n·ap
=am+n+pam·an·ap=am ·(an·ap )=am·ap +n=am+n+p或方法2 am·an·ap=am+n+p=(10×10)×(10×10×10)=10×10×10×10×10=105(1)(根据 。)(根据 。)(根据 。)乘法结合律幂的意义幂的意义=102+3随堂练习P:14 整式加减的结果还是最简整式。所谓最简整式,即这个整式中不再有同类项和括号;而在合并同类项之前,相加减的整式之间可能有括号。1.整式加减的法则是什么?2.整式的加减实际上就是做什么?3.整式的加减一般步骤是什么?4.整式的加减的结果是什么?去括号,再合并同类项;整式的加减实际上就是合并同类项;一般步骤是先去括号,再合并同类项;回顾与思考 7.探究型题有时可从数量关系表示
的规律着手,也可从图形本身和
规律着手.5.整式加减运算的易错处是:6.用字母、代数式表示问题结果时;
化简中有时用到整式的加减; 去括号时漏乘、符号的变与不变; 幂的意义
幂的意义(根据 。)(根据 。)(根据 。)乘法结合律解:100 × 3×105 × 3×107 =
9 × 1014例2。我国自行研制的神威一号计算机的峰值运算速度达到每秒3840亿次,如果按这个速度工作一天,那么它能运算多少次(结果保留3 个有效数字)?解:3840亿次=3.84 × 103 ×10824小时=24 ×3.6 × 103(3.84 × 103 × 108 ) × (24 ×3.6 × 103 )
=
=
=( 3.84 × 24 ×3.6 ) × ( 103 × 108 × 103 )
331 . 776 × 10143 . 32 × 1016(次)答:它一天约能运算3 . 32 × 1016次
(3) x4+x4=x8 ( ) (3)x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5= -x5 ( )
(6)a2·a3- a3·a2 = 0 ( )
(7)x3·y5=(xy)8 ( ) (8) x7+x7=x14 ( )
√√××××××例1 计算:⑴108 ×103;⑶76 ×74;例2 化简:⑴(-2)8 ×(-2)7;⑵⑶想一想am · an · ap 等于什么?例2。我国自行研制的神威一号计算机的峰值运算速度达到每秒3840亿次,如果按这个速度工作一天,那么它能运算多少次(结果保留3 个有效数字)?解:3840亿次=3.84 × 103 ×10824小时=24 ×3.6 × 103(3.84 × 103 × 108 ) × (24 ×3.6 × 103 )
=
=
=( 3.84 × 24 ×3.6 ) × ( 103 × 108 × 103 )
331 . 776 × 10143 . 32 × 1016(次)答:它一天约能运算3 . 32 × 1016次同底数幂的乘法性质:底数 ,指数 .不变相加幂的意义:小 结做一做1、计算下列各式:
(1)102×103
(2)105×108
(3)10m×10n(m,n都是正整数).你发现了什么? 2. 2m×2n等于什么?(1/7)m×(1/7)n 呢?
(m,n 都是正整数)=2m+n=(2×2×···×2)×(2×2×···×2) m个2 n个22m×2n2、 (1/7)m ×(1/7)n= (1/7)m+n方法1 am·an·ap
=(am·an)·ap=am+n·ap
=am+n+pam·an·ap=am ·(an·ap )=am·ap +n=am+n+p或方法2 am·an·ap=am+n+p=(10×10)×(10×10×10)=10×10×10×10×10=105(1)(根据 。)(根据 。)(根据 。)乘法结合律幂的意义幂的意义=102+3随堂练习P:14 整式加减的结果还是最简整式。所谓最简整式,即这个整式中不再有同类项和括号;而在合并同类项之前,相加减的整式之间可能有括号。1.整式加减的法则是什么?2.整式的加减实际上就是做什么?3.整式的加减一般步骤是什么?4.整式的加减的结果是什么?去括号,再合并同类项;整式的加减实际上就是合并同类项;一般步骤是先去括号,再合并同类项;回顾与思考 7.探究型题有时可从数量关系表示
的规律着手,也可从图形本身和
规律着手.5.整式加减运算的易错处是:6.用字母、代数式表示问题结果时;
化简中有时用到整式的加减; 去括号时漏乘、符号的变与不变; 幂的意义
幂的意义(根据 。)(根据 。)(根据 。)乘法结合律解:100 × 3×105 × 3×107 =
9 × 1014例2。我国自行研制的神威一号计算机的峰值运算速度达到每秒3840亿次,如果按这个速度工作一天,那么它能运算多少次(结果保留3 个有效数字)?解:3840亿次=3.84 × 103 ×10824小时=24 ×3.6 × 103(3.84 × 103 × 108 ) × (24 ×3.6 × 103 )
=
=
=( 3.84 × 24 ×3.6 ) × ( 103 × 108 × 103 )
331 . 776 × 10143 . 32 × 1016(次)答:它一天约能运算3 . 32 × 1016次
