2.6一元一次不等式组 导学案1(含答案)八年级数学下册北师大版
文档属性
| 名称 | 2.6一元一次不等式组 导学案1(含答案)八年级数学下册北师大版 |  | |
| 格式 | doc | ||
| 文件大小 | 477.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 11:08:27 | ||
图片预览


文档简介
2.6一元一次不等式组
预习案
一、学习目标
1.理解一元一次不等式组及的解集等概念;并会解由两个一元一次不等式组成的不等式组,会用数轴确定解集。
2.能运用不等式组解决简单的实际问题,培养学生独立思考的习惯和合作交流意识。
3.培养学生学会分析问题、解决问题的良好习惯。
二、预习内容
1.阅读课本第54-59页
2.一元一次不等式组的解法:设a<b,那么
(1)不等式组的解集是x>b; (2)不等式组的解集是x<a;
(3)不等式组的解集是a<x<b; (4)不等式组的解集是无解.
这是用式子表示,也可以用语言简单表述为:同大取大;同小取小;大小小大中间找;大大小小找不到。
3.一元一次不等式组巩固练习:
不等式组 用数轴表示不等式①、②的解集 不等式组的解集
x>2 ①x>3 ② 0 2 3
x<2 ①x<3 ②
x>2 ①x<3 ②
x >2 ①x≤3 ②
x<2 ①x>3 ②
三、预习检测
1.下列式子是一元一次不等式组的是( )
2. 列不等式组解集正确的是( )
3. 解不等式组:
(1)
(2)
探究案
一、合作探究(9分钟),要求各小组组长组织成员进行合作探究、讨论。
探究:一元一次不等式解集推导过程:
1、结合图形,填写下表,与同学交流。
思考:图中不等式组的解集?
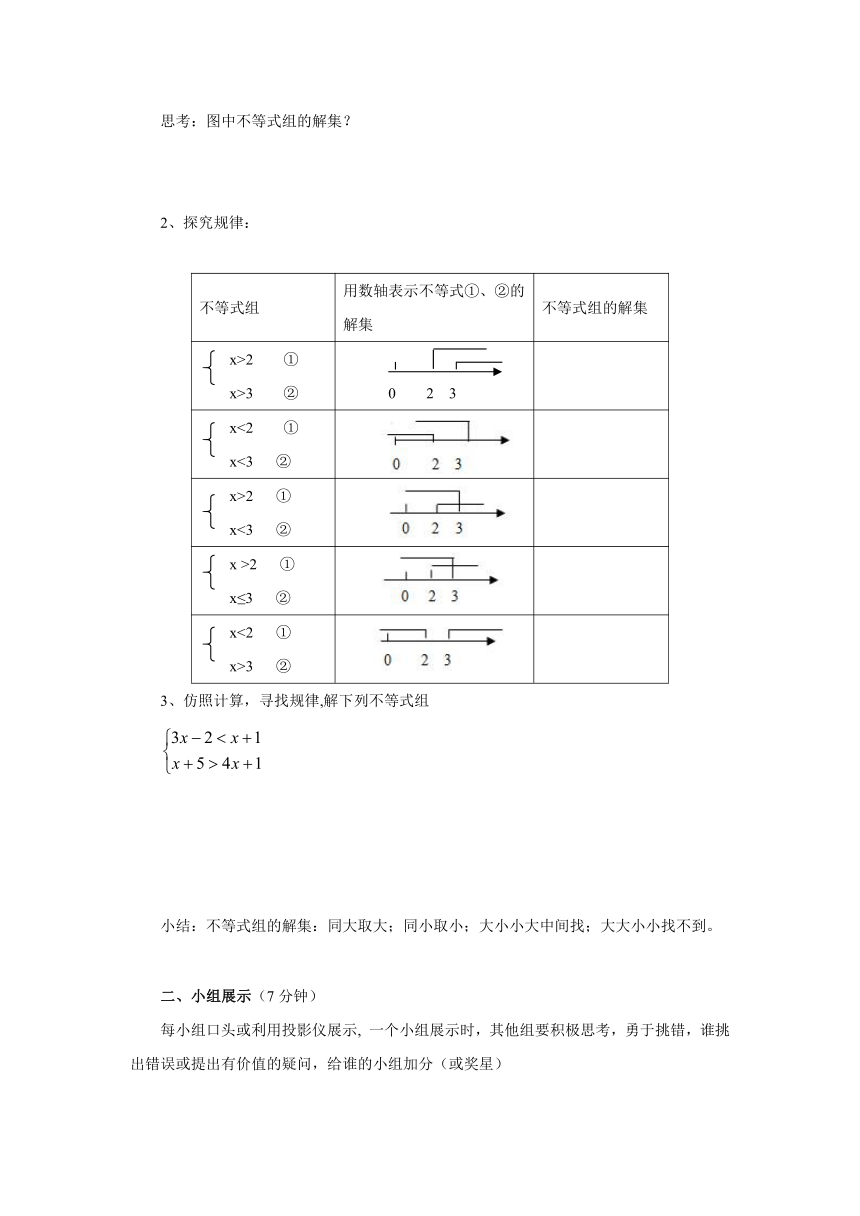
2、探究规律:
不等式组 用数轴表示不等式①、②的解集 不等式组的解集
x>2 ①x>3 ② 0 2 3
x<2 ①x<3 ②
x>2 ①x<3 ②
x >2 ①x≤3 ②
x<2 ①x>3 ②
3、仿照计算,寻找规律,解下列不等式组
小结:不等式组的解集:同大取大;同小取小;大小小大中间找;大大小小找不到。
二、小组展示(7分钟)
每小组口头或利用投影仪展示, 一个小组展示时,其他组要积极思考,勇于挑错,谁挑出错误或提出有价值的疑问,给谁的小组加分(或奖星)
交流内容 展示小组(随机) 点评小组(随机)
____________ 第______组 第______组
____________ 第______组 第______组
三、归纳总结
本节课学习了完全平方公式,通过观察、对比、推断、交流、归纳等方式.重点学习完全平方公式,并能够正确地运用完全平方公式进行整式的乘法的有关运算,解决了生活和数学中的一些简单问题。(要求:将本节课的知识和解决问题的方法梳理一下)
四、课堂达标检测
1.等式组的解集在下列数轴上表示正确的是( )
A.
B.
C.
D.
2.若点A(m-3,1-3m)在第三象限,则m的取值范围是( )
A. B.m<3 C.m>3 D.
3.不等式组的解集是( )
A.1<x≤2 B.﹣1<x≤2 C.x>﹣1 D.﹣1<x≤4
4.使不等式x﹣1≥2与3x﹣7<8同时成立的x的整数值是( )
A.3,4 B.4,5 C.3,4,5 D.不存在
5.不等式组的所有整数解的和是( )
A.2 B.3 C.5 D.6
五、学习反馈
本节课你学到了什么?有什么收获和体会?还有什么困惑?
参考答案
预习检测
1、B
2、D
3、
课堂达标检测
1. B
解析:不等式可化为:.
在数轴上表示为:
2. D
解析:根据题意可知,解不等式组得,即.故选D.
3. B
4. A
解析:根据题意得:,解得:3≤x<5,则x的整数值是3,4;故选A.
5. D
解析:【解答】
∵解不等式①得;x>﹣,
解不等式②得;x≤3,
∴不等式组的解集为﹣<x≤3,
∴不等式组的整数解为0,1,2,3,
0+1+2+3=6,
故选D.
预习案
一、学习目标
1.理解一元一次不等式组及的解集等概念;并会解由两个一元一次不等式组成的不等式组,会用数轴确定解集。
2.能运用不等式组解决简单的实际问题,培养学生独立思考的习惯和合作交流意识。
3.培养学生学会分析问题、解决问题的良好习惯。
二、预习内容
1.阅读课本第54-59页
2.一元一次不等式组的解法:设a<b,那么
(1)不等式组的解集是x>b; (2)不等式组的解集是x<a;
(3)不等式组的解集是a<x<b; (4)不等式组的解集是无解.
这是用式子表示,也可以用语言简单表述为:同大取大;同小取小;大小小大中间找;大大小小找不到。
3.一元一次不等式组巩固练习:
不等式组 用数轴表示不等式①、②的解集 不等式组的解集
x>2 ①x>3 ② 0 2 3
x<2 ①x<3 ②
x>2 ①x<3 ②
x >2 ①x≤3 ②
x<2 ①x>3 ②
三、预习检测
1.下列式子是一元一次不等式组的是( )
2. 列不等式组解集正确的是( )
3. 解不等式组:
(1)
(2)
探究案
一、合作探究(9分钟),要求各小组组长组织成员进行合作探究、讨论。
探究:一元一次不等式解集推导过程:
1、结合图形,填写下表,与同学交流。
思考:图中不等式组的解集?
2、探究规律:
不等式组 用数轴表示不等式①、②的解集 不等式组的解集
x>2 ①x>3 ② 0 2 3
x<2 ①x<3 ②
x>2 ①x<3 ②
x >2 ①x≤3 ②
x<2 ①x>3 ②
3、仿照计算,寻找规律,解下列不等式组
小结:不等式组的解集:同大取大;同小取小;大小小大中间找;大大小小找不到。
二、小组展示(7分钟)
每小组口头或利用投影仪展示, 一个小组展示时,其他组要积极思考,勇于挑错,谁挑出错误或提出有价值的疑问,给谁的小组加分(或奖星)
交流内容 展示小组(随机) 点评小组(随机)
____________ 第______组 第______组
____________ 第______组 第______组
三、归纳总结
本节课学习了完全平方公式,通过观察、对比、推断、交流、归纳等方式.重点学习完全平方公式,并能够正确地运用完全平方公式进行整式的乘法的有关运算,解决了生活和数学中的一些简单问题。(要求:将本节课的知识和解决问题的方法梳理一下)
四、课堂达标检测
1.等式组的解集在下列数轴上表示正确的是( )
A.
B.
C.
D.
2.若点A(m-3,1-3m)在第三象限,则m的取值范围是( )
A. B.m<3 C.m>3 D.
3.不等式组的解集是( )
A.1<x≤2 B.﹣1<x≤2 C.x>﹣1 D.﹣1<x≤4
4.使不等式x﹣1≥2与3x﹣7<8同时成立的x的整数值是( )
A.3,4 B.4,5 C.3,4,5 D.不存在
5.不等式组的所有整数解的和是( )
A.2 B.3 C.5 D.6
五、学习反馈
本节课你学到了什么?有什么收获和体会?还有什么困惑?
参考答案
预习检测
1、B
2、D
3、
课堂达标检测
1. B
解析:不等式可化为:.
在数轴上表示为:
2. D
解析:根据题意可知,解不等式组得,即.故选D.
3. B
4. A
解析:根据题意得:,解得:3≤x<5,则x的整数值是3,4;故选A.
5. D
解析:【解答】
∵解不等式①得;x>﹣,
解不等式②得;x≤3,
∴不等式组的解集为﹣<x≤3,
∴不等式组的整数解为0,1,2,3,
0+1+2+3=6,
故选D.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
