江西省宜春市重点中学2022-2023学年高二下学期期中考试数学试题(含解析)
文档属性
| 名称 | 江西省宜春市重点中学2022-2023学年高二下学期期中考试数学试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 590.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 13:10:53 | ||
图片预览




文档简介
宜春市重点中学2022-2023学年高二下学期期中考试
数学试卷
注意事项:
1. 答题前填写好自己的姓名、班级、考号等信息
2. 请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每小题5分,共40分)
1. 设f(x)在处可导,则( )
A.() B.() C. f'() D. f'()
2. 小智和电脑连续下两盘棋,已知小智第一盘获胜的概率是0.5,小智连续两盘都获胜的概率是0.4,那么小智在第一盘获胜的条件下,第二盘也获胜的概率是( )
A. 0.4 B. 0.8 C. 0.2 D. 0.5
3. 设等比数列{}的前n项和为,若,且,,成等差数列,则=( )
A. 63 B. 31 C. -63 D. -31
4. 已知数列{}的通项为,则其前8项和为( )
A. B. C. D.
5. 某课外兴趣小组通过随机调查,利用列联表和统计量研究数学成绩优秀是否与性别有关。计算得,经查阅临界值表知P,则下列判断正确的是( )
A. 每100个数学成绩优秀的人中就会有1名是女生
B. 若某人数学成绩优秀,那么他为男生的概率是0.010
C. 有99%的把握认为“数学成绩优秀与性别无关”
D. 在犯错误的概率不超过1%的前提下认为“数学成绩优秀与性别有关”
6. “二十四节气”是上古农耕文明的产物,它是上古先民顺应农时,通过观察天体运行,认知一岁中时令、气候、物候等变化规律所形成的知识体系。我国古代用日晷测量日影的长度,晷长即为所测量影子的长度二十四个节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,冬至日晷长最长,夏至日晷长最短,周而复始,已知冬至日晷长为13.5尺,芒种日晷长为2.5尺,则一年中立春到夏至的日晷长的和为( )
A. 58.5尺 B. 59.5尺 C. 60尺 D. 60.5尺
7. 在等差数列{}中,若是方程的两根,则{}的前12项的和为( )
A. 12 B. 18 C. -18 D. -12
8. 已知定义在R上的偶函数f(x)的导函数为f'(x),当时,有,且,则使得成立的x的取值范围是( )
A. B. C. (-1,0)∪(1,) D.
二、多选题(每小题5分,共20分)
9. 若{}为等差数列,,则下列说法正确的是( )
A. B. -20是数列{}中的项
C. 数列{}单调递减 D. 数列{}前7项和最大
10. 下列求导运算正确的是( )
A. B.
C. D.
11. 如图是函数的导函数的图象,对于下列四个判断,其中正确的是( )
A. f(x)在(-2,-1)上是增函数 B. f(x)在(2,4)上是减函数
C. 当时,f(x)取得极小值 D. 当时,f(x)取得极大值
12. 已知函数,下列说法正确的有( )
A. f(x)的极大值为 B. f(x)的单调递减区间为(0,)
C. 曲线在处的切线方程为 D. 方程有两个不同的解
第II卷(非选择题)
三、填空题(每小题5分,共20分)
13. 已知,则___________。
14. 在等比数列{}中,,是函数的极值点,则=___________。
15. 若函数在区间[-1,1]上单调递减,则实数m的取值范围为___________。
16. 已知函数对一切恒成立,则a的取值范围是___________。
四、解答题(第17题10分,其它每题12分,共70分)
17. 已知数列{}满足:
(1)求证:数列是等比数列;
(2)求数列{}的通项公式及其前n项和的表达式。
18. 已知函数,
(1)当时,求曲线在点(3,f(3))处的切线方程;
(2)讨论f(x)的单调性。
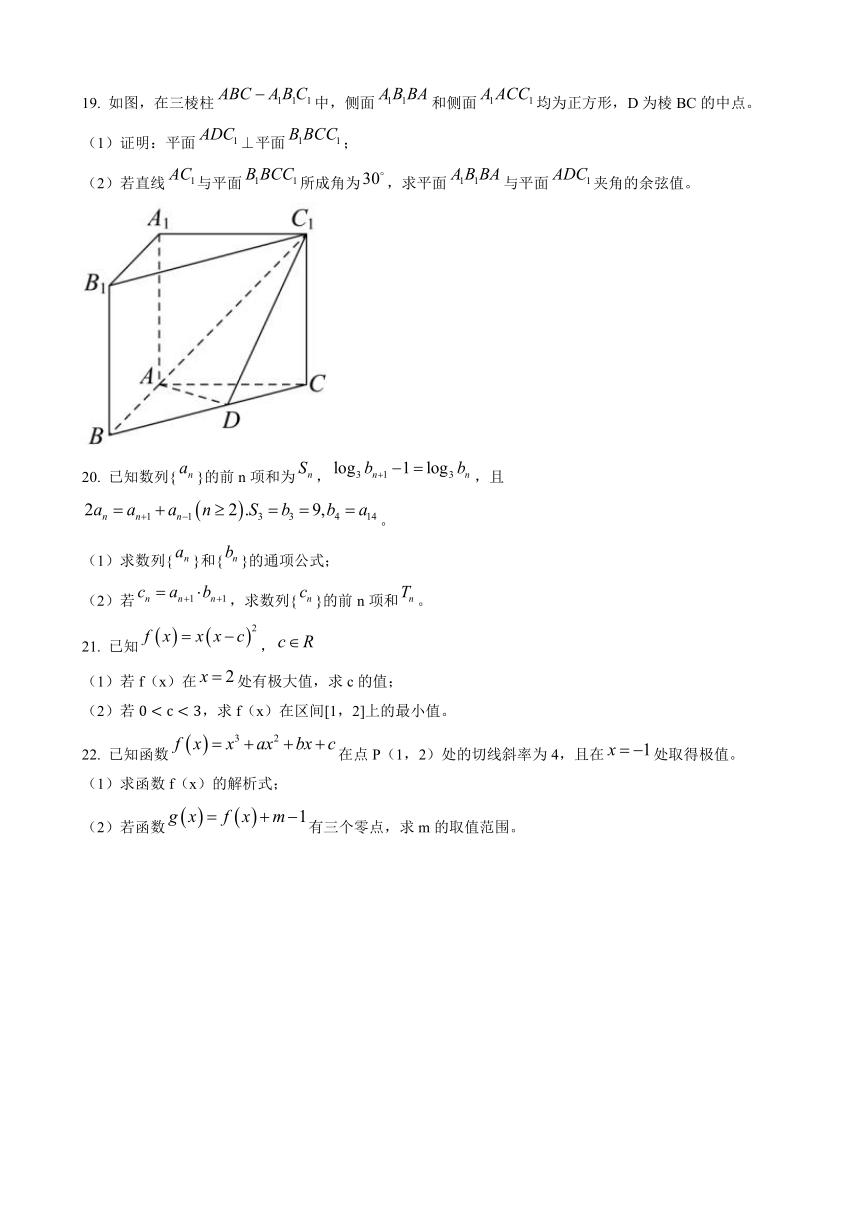
19. 如图,在三棱柱中,侧面和侧面均为正方形,D为棱BC的中点。
(1)证明:平面⊥平面;
(2)若直线与平面所成角为,求平面与平面夹角的余弦值。
20. 已知数列{}的前n项和为,,且。
(1)求数列{}和{}的通项公式;
(2)若,求数列{}的前n项和。
21. 已知,
(1)若f(x)在处有极大值,求c的值;
(2)若,求f(x)在区间[1,2]上的最小值。
22. 已知函数在点P(1,2)处的切线斜率为4,且在处取得极值。
(1)求函数f(x)的解析式;
(2)若函数有三个零点,求m的取值范围。
数学试卷
参考答案
1. C
【分析】变形结合导数的定义,计算出结果。
【详解】因为f(x)在处可导,
所以,由导数的定义可得:
故选:C。
2. B
【分析】记事件A:小智第一盘获胜,事件B:小智第二盘获胜,根据题意可得出P(A)、P(AB),利用条件概率公式可求得所求事件的概率。
【详解】记事件A:小智第一盘获胜,事件B:小智第二盘获胜,则
因此,小智在第一盘获胜的条件下,第二盘也获胜的概率是,
故选:B。
3. A
【分析】设出公比,根据成等差数列列出方程,求出公比,利用等比求和公式求出答案.
【详解】设公比为,
因为成等差数列,所以,
则,解得:或0(舍去)。
因为,所以,故。
故选:A。
4. D
【分析】运用裂项相消法进行求解即可。
【详解】,
所以前8项和为,
故选:D
5. D
【分析】计算K的观测值,对照阅临界值表知,即可得出统计结论。
【详解】∵,∴有99%的把握认为“数学成绩优秀与性别有关”,即在犯错误的概率不超过1%的前提下认为“数学成绩优秀与性别有关”。所以ABC错误,
故选:D
6. C
【分析】根据等差数列的通项公式和前n项和公式进行求解即可。
【详解】设冬至日晷长为,小寒日晷长为,以此类推芒种日晷长为,
因此,,设从冬至日到夏至日过程中,晷长的变化量为d,
所以有,立春日晷长为,
夏至的日晷长为,
所以一年中立春到夏至的日晷长的和为,
故选:C。
7. D
【分析】利用韦达定理得出,利用等差数列的求和公式以及等差数列下标和的性质可求得结果。【详解】因为,是方程的两根,
由韦达定理可得,
所以等差数列{}的前12项的和。
故选:D。
8. A
【分析】根据当时,有,令,得到g(x)在(0,+∞)上递增,再根据f(x)在R上的偶函数,得到g(x)在R上是奇函数,则g(x)在(-∞,0)上递增,然后由,得到求解。
【详解】因为当时,有,
令,
所以,
所以g(x)在(0,+∞)上递增,
又因为f(x)在R上的偶函数
所以
所以g(x)在R上是奇函数
所以g(x)在(-∞,0)上递增,
又因为,
所以,
当时,,此时,,
当,时,,此时,,
所以成立的x的取值范围是
故选:A。
【点睛】本题主要考查导数与函数的单调性以及利用单调性解不等式,还考查了转化化归的思想和推理求解的能力,属于中档题
9. ACD
【分析】由{}为等差数列,列方程组求得首项与公差,就可得到通项公式,然后对选项逐一判断即可。
【详解】因为数列{}为等差数列,且,则,解得,故A选项正确,
由,得,故B错误,
因为,所以数列{}单调递减,故C正确,
由数列通项公式可知,前7项均为正数,,所以前7项和最大,故D正确。
故选:ACD
10. AB
【分析】根据导数运算法则依次讨论求解即可;
【详解】解:对于A选项,,故正确;
对于B选项,,故正确;
对于C选项,,故错误;
对于D选项,,故错误;
故选:AB。
11. BC
【分析】根据导数与原函数关系解决。
【详解】从导函数图像可以看出函数f(x)在(-2,-1),(2,4)上为单调减函数;
f(x)在(-1,2),(4,5)上为增函数,故A错B对,C对D错。
故选:BC
12. BC
【分析】利用导数,求f(x)的单调区间和极值,验证选项AB,由导数的几何意义求曲线在处的切线方程,判断选项C,数形结合求方程解的个数,判断选项D.
【详解】函数,定义域为(0,+∞),
,解得,,解得
f(x)在(0,)上单调递减,在上单调递增,B选项正确;
f(x)有极小值,无极大值,A选项错误;
由,曲线在处的切点为(1,0),切线斜率为1,切线方程为,C选项正确;
,即1n,函数与的图像在(0,+∞)上只有一个交点,所以方程有一个解,D选项错误。
故选:BC
13. -63
【分析】通过赋值法可得结果
【详解】令,则,即,
令,则。
故答案为:-63
14. 2
【分析】由题,利用导数及韦达定理可得,后利用等比中项性质可得答案。
【详解】,
由题,是方程的两个不等实根,
则由韦达定理,所以
又是,的等比中项且与,同号,则。
故答案为:2。
15. (-∞,-2]
【分析】由题意得到在[-1,1]上恒成立,参变分离,只需,求出,从而得到答案。
【详解】,
由题意得在[-1,1]上恒成立,
因为,所以在[-1,1]上恒成立,
即在[-1,1]上恒成立,只需,
其中,所以,
故答案为:(-∞,-2]
16. (-∞,4]
【分析】根据题意,通过分离参数法得出在上恒成立,再构造函数,利用导数研究函数的单调性和最值,求出,进而求得a的取值范围。
【详解】解:由题可知,,即,
得在上恒成立,
设
则,
当时,,h(x)单调递减,
当时,,h(x)单调递增。
∴,
∴,
即a的取值范围是(-∞,4]
故答案为:(-∞,4]。
17.(1)证明见解析;
(2)
【分析】(1)由等比数列的定义证明即可;
(2)由(1)得出数列{}的通项公式,再由等差和等比的求和公式计算。
【详解】(1)由题意可知
所以数列是以3为首项,公比为3的等比数列。
(2)由(1)可知,,即
前n项和
18. (1)
(2)答案见解析
【分析】(1)由导数几何意义可求得切线斜率f'(3),结合可得切线方程;
(2)求导后,分别在和的情况下,根据(x)正负得到函数单调性。
【详解】(1)当时,,则,∴,又,
∴f(x)在点(3,f(3))处的切线方程为:,即。
(2)由题意得:f(x)定义域为R,
当时,,f(x)在R上单调递增;
当时,若,则;若,则
∴f(x)在(-∞,a),(0,+∞)上单调递增,在(a,0)上单调递减;
当时,若,则;若,则
∴f(x)在(-∞,0),(a,+∞)上单调递增,在(0,a)上单调递减;
综上所述:当时,f(x)在R上单调递增;
当时,f(x)在(-∞,a),(0,+∞)上单调递增,在(a,0)上单调递减;
当时,f(x)在(-∞,0),(a,+∞)上单调递增,在(0,a)上单调递减
19.(1)证明见解析
(2)
【分析】(1)根据线面垂直的判定定理可得A1A⊥平面ABC,即平面ABC,进而,再次利用线面垂直的判定定理可得AD⊥平面,结合面面垂直的判定定理即可证明;
(2) 建立如图空间直角坐标系,利用向量法求出平面的法向量,结合面面角的向量求法即得。
【详解】(1)因为侧面、侧面均为正方形,
所以,,又,AB、AC 平面ABC,
所以A1A⊥平面ABC,又,所以平面ABC,
又AD 平面ABC,所以
由,D为棱BC的中点,所以,
又,BC、 平面,
因此AD⊥平面,又AD 平面,
故平面⊥平面;
(2)由(1)得是与侧面所成角,即,令,所以,又,
所以,,则,。
以A为原点,以,,分别为x轴,y轴,z轴的正方向,建立如图所 x示空间直角坐标系,
则A(0,0,0),D(1,1,0),(0,2,2)。所以。
设是平面的一个法向量,
则即取
易知是平面的一个法向量,则
而平面与平面的夹角为锐角,
所以平面与平面的夹角的余弦值为。
20. (1),
(2)
【分析】(1)根据对数运算得,利用等比数列定义求通项公式,利用等差中项判断数列}为等差数列,建立方程求出公差,从而可得}的通项;
(2)利用错位相减法计算即可。
【详解】(1)∵,∴,则,所以{}为等比数列,又,得,所以,
由知{}是等差数列,且
∴,得∴
(2)因为,,所以,
所以
则
上面两式作差得
,
∴
21. (1)
(2)
【分析】(1)求出,令,解得c,再分别讨论,利用函数f(x)在处有极大值,从而得出答案;
(2)确定函数的单调性,即可求f(x)在区间[1,2]上的最小值。
【详解】(1)由题知,
由题意,,得或,
当时,在,在(,2)上
此时,f(x)在处有极小值,不符题意;
当时,在,在(2,6)上;
此时,f(x)在处有极大值,符合题意。
综上,。
(2) 令,得或,
由,则在上,在(,c)上
即f(x)在上单调递增,在(,c)上单调递减。
由题意,
当时,f(x)在区间[1,2]上单调递减,则,
当时,f(x)在区间(1,c)上单调递减,在(c,2)上单调递增,则,
当时,f(x)在区间[1,2]上单调递增,则,
综上,
22. (1)
(2)(-1,)
【分析】(1)根据题意,列出方程组求得,求导,利用导数判断f(x)的单调性与极值;
(2)由题意得到原题意等价于与有三个交点,结合(1)中f(x)的单调性与极值,列式求解。
【详解】(1)∵
由题意得,解得,
所以,
令,解得或;令,解得
则上单调递增,在(-1,)上单调递减,
∴f(x)在处取到极大值,在处取到极小值,
故符合题意,
(2) 令,则,
原题意等价于与有三个交点,
由(1)可得:上单调递增,在(-1,)上单调递减,
∴f(x)在处取到极大值,在处取到极小值,
故,解得
所以m的取值范围为
数学试卷
注意事项:
1. 答题前填写好自己的姓名、班级、考号等信息
2. 请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每小题5分,共40分)
1. 设f(x)在处可导,则( )
A.() B.() C. f'() D. f'()
2. 小智和电脑连续下两盘棋,已知小智第一盘获胜的概率是0.5,小智连续两盘都获胜的概率是0.4,那么小智在第一盘获胜的条件下,第二盘也获胜的概率是( )
A. 0.4 B. 0.8 C. 0.2 D. 0.5
3. 设等比数列{}的前n项和为,若,且,,成等差数列,则=( )
A. 63 B. 31 C. -63 D. -31
4. 已知数列{}的通项为,则其前8项和为( )
A. B. C. D.
5. 某课外兴趣小组通过随机调查,利用列联表和统计量研究数学成绩优秀是否与性别有关。计算得,经查阅临界值表知P,则下列判断正确的是( )
A. 每100个数学成绩优秀的人中就会有1名是女生
B. 若某人数学成绩优秀,那么他为男生的概率是0.010
C. 有99%的把握认为“数学成绩优秀与性别无关”
D. 在犯错误的概率不超过1%的前提下认为“数学成绩优秀与性别有关”
6. “二十四节气”是上古农耕文明的产物,它是上古先民顺应农时,通过观察天体运行,认知一岁中时令、气候、物候等变化规律所形成的知识体系。我国古代用日晷测量日影的长度,晷长即为所测量影子的长度二十四个节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,冬至日晷长最长,夏至日晷长最短,周而复始,已知冬至日晷长为13.5尺,芒种日晷长为2.5尺,则一年中立春到夏至的日晷长的和为( )
A. 58.5尺 B. 59.5尺 C. 60尺 D. 60.5尺
7. 在等差数列{}中,若是方程的两根,则{}的前12项的和为( )
A. 12 B. 18 C. -18 D. -12
8. 已知定义在R上的偶函数f(x)的导函数为f'(x),当时,有,且,则使得成立的x的取值范围是( )
A. B. C. (-1,0)∪(1,) D.
二、多选题(每小题5分,共20分)
9. 若{}为等差数列,,则下列说法正确的是( )
A. B. -20是数列{}中的项
C. 数列{}单调递减 D. 数列{}前7项和最大
10. 下列求导运算正确的是( )
A. B.
C. D.
11. 如图是函数的导函数的图象,对于下列四个判断,其中正确的是( )
A. f(x)在(-2,-1)上是增函数 B. f(x)在(2,4)上是减函数
C. 当时,f(x)取得极小值 D. 当时,f(x)取得极大值
12. 已知函数,下列说法正确的有( )
A. f(x)的极大值为 B. f(x)的单调递减区间为(0,)
C. 曲线在处的切线方程为 D. 方程有两个不同的解
第II卷(非选择题)
三、填空题(每小题5分,共20分)
13. 已知,则___________。
14. 在等比数列{}中,,是函数的极值点,则=___________。
15. 若函数在区间[-1,1]上单调递减,则实数m的取值范围为___________。
16. 已知函数对一切恒成立,则a的取值范围是___________。
四、解答题(第17题10分,其它每题12分,共70分)
17. 已知数列{}满足:
(1)求证:数列是等比数列;
(2)求数列{}的通项公式及其前n项和的表达式。
18. 已知函数,
(1)当时,求曲线在点(3,f(3))处的切线方程;
(2)讨论f(x)的单调性。
19. 如图,在三棱柱中,侧面和侧面均为正方形,D为棱BC的中点。
(1)证明:平面⊥平面;
(2)若直线与平面所成角为,求平面与平面夹角的余弦值。
20. 已知数列{}的前n项和为,,且。
(1)求数列{}和{}的通项公式;
(2)若,求数列{}的前n项和。
21. 已知,
(1)若f(x)在处有极大值,求c的值;
(2)若,求f(x)在区间[1,2]上的最小值。
22. 已知函数在点P(1,2)处的切线斜率为4,且在处取得极值。
(1)求函数f(x)的解析式;
(2)若函数有三个零点,求m的取值范围。
数学试卷
参考答案
1. C
【分析】变形结合导数的定义,计算出结果。
【详解】因为f(x)在处可导,
所以,由导数的定义可得:
故选:C。
2. B
【分析】记事件A:小智第一盘获胜,事件B:小智第二盘获胜,根据题意可得出P(A)、P(AB),利用条件概率公式可求得所求事件的概率。
【详解】记事件A:小智第一盘获胜,事件B:小智第二盘获胜,则
因此,小智在第一盘获胜的条件下,第二盘也获胜的概率是,
故选:B。
3. A
【分析】设出公比,根据成等差数列列出方程,求出公比,利用等比求和公式求出答案.
【详解】设公比为,
因为成等差数列,所以,
则,解得:或0(舍去)。
因为,所以,故。
故选:A。
4. D
【分析】运用裂项相消法进行求解即可。
【详解】,
所以前8项和为,
故选:D
5. D
【分析】计算K的观测值,对照阅临界值表知,即可得出统计结论。
【详解】∵,∴有99%的把握认为“数学成绩优秀与性别有关”,即在犯错误的概率不超过1%的前提下认为“数学成绩优秀与性别有关”。所以ABC错误,
故选:D
6. C
【分析】根据等差数列的通项公式和前n项和公式进行求解即可。
【详解】设冬至日晷长为,小寒日晷长为,以此类推芒种日晷长为,
因此,,设从冬至日到夏至日过程中,晷长的变化量为d,
所以有,立春日晷长为,
夏至的日晷长为,
所以一年中立春到夏至的日晷长的和为,
故选:C。
7. D
【分析】利用韦达定理得出,利用等差数列的求和公式以及等差数列下标和的性质可求得结果。【详解】因为,是方程的两根,
由韦达定理可得,
所以等差数列{}的前12项的和。
故选:D。
8. A
【分析】根据当时,有,令,得到g(x)在(0,+∞)上递增,再根据f(x)在R上的偶函数,得到g(x)在R上是奇函数,则g(x)在(-∞,0)上递增,然后由,得到求解。
【详解】因为当时,有,
令,
所以,
所以g(x)在(0,+∞)上递增,
又因为f(x)在R上的偶函数
所以
所以g(x)在R上是奇函数
所以g(x)在(-∞,0)上递增,
又因为,
所以,
当时,,此时,,
当,时,,此时,,
所以成立的x的取值范围是
故选:A。
【点睛】本题主要考查导数与函数的单调性以及利用单调性解不等式,还考查了转化化归的思想和推理求解的能力,属于中档题
9. ACD
【分析】由{}为等差数列,列方程组求得首项与公差,就可得到通项公式,然后对选项逐一判断即可。
【详解】因为数列{}为等差数列,且,则,解得,故A选项正确,
由,得,故B错误,
因为,所以数列{}单调递减,故C正确,
由数列通项公式可知,前7项均为正数,,所以前7项和最大,故D正确。
故选:ACD
10. AB
【分析】根据导数运算法则依次讨论求解即可;
【详解】解:对于A选项,,故正确;
对于B选项,,故正确;
对于C选项,,故错误;
对于D选项,,故错误;
故选:AB。
11. BC
【分析】根据导数与原函数关系解决。
【详解】从导函数图像可以看出函数f(x)在(-2,-1),(2,4)上为单调减函数;
f(x)在(-1,2),(4,5)上为增函数,故A错B对,C对D错。
故选:BC
12. BC
【分析】利用导数,求f(x)的单调区间和极值,验证选项AB,由导数的几何意义求曲线在处的切线方程,判断选项C,数形结合求方程解的个数,判断选项D.
【详解】函数,定义域为(0,+∞),
,解得,,解得
f(x)在(0,)上单调递减,在上单调递增,B选项正确;
f(x)有极小值,无极大值,A选项错误;
由,曲线在处的切点为(1,0),切线斜率为1,切线方程为,C选项正确;
,即1n,函数与的图像在(0,+∞)上只有一个交点,所以方程有一个解,D选项错误。
故选:BC
13. -63
【分析】通过赋值法可得结果
【详解】令,则,即,
令,则。
故答案为:-63
14. 2
【分析】由题,利用导数及韦达定理可得,后利用等比中项性质可得答案。
【详解】,
由题,是方程的两个不等实根,
则由韦达定理,所以
又是,的等比中项且与,同号,则。
故答案为:2。
15. (-∞,-2]
【分析】由题意得到在[-1,1]上恒成立,参变分离,只需,求出,从而得到答案。
【详解】,
由题意得在[-1,1]上恒成立,
因为,所以在[-1,1]上恒成立,
即在[-1,1]上恒成立,只需,
其中,所以,
故答案为:(-∞,-2]
16. (-∞,4]
【分析】根据题意,通过分离参数法得出在上恒成立,再构造函数,利用导数研究函数的单调性和最值,求出,进而求得a的取值范围。
【详解】解:由题可知,,即,
得在上恒成立,
设
则,
当时,,h(x)单调递减,
当时,,h(x)单调递增。
∴,
∴,
即a的取值范围是(-∞,4]
故答案为:(-∞,4]。
17.(1)证明见解析;
(2)
【分析】(1)由等比数列的定义证明即可;
(2)由(1)得出数列{}的通项公式,再由等差和等比的求和公式计算。
【详解】(1)由题意可知
所以数列是以3为首项,公比为3的等比数列。
(2)由(1)可知,,即
前n项和
18. (1)
(2)答案见解析
【分析】(1)由导数几何意义可求得切线斜率f'(3),结合可得切线方程;
(2)求导后,分别在和的情况下,根据(x)正负得到函数单调性。
【详解】(1)当时,,则,∴,又,
∴f(x)在点(3,f(3))处的切线方程为:,即。
(2)由题意得:f(x)定义域为R,
当时,,f(x)在R上单调递增;
当时,若,则;若,则
∴f(x)在(-∞,a),(0,+∞)上单调递增,在(a,0)上单调递减;
当时,若,则;若,则
∴f(x)在(-∞,0),(a,+∞)上单调递增,在(0,a)上单调递减;
综上所述:当时,f(x)在R上单调递增;
当时,f(x)在(-∞,a),(0,+∞)上单调递增,在(a,0)上单调递减;
当时,f(x)在(-∞,0),(a,+∞)上单调递增,在(0,a)上单调递减
19.(1)证明见解析
(2)
【分析】(1)根据线面垂直的判定定理可得A1A⊥平面ABC,即平面ABC,进而,再次利用线面垂直的判定定理可得AD⊥平面,结合面面垂直的判定定理即可证明;
(2) 建立如图空间直角坐标系,利用向量法求出平面的法向量,结合面面角的向量求法即得。
【详解】(1)因为侧面、侧面均为正方形,
所以,,又,AB、AC 平面ABC,
所以A1A⊥平面ABC,又,所以平面ABC,
又AD 平面ABC,所以
由,D为棱BC的中点,所以,
又,BC、 平面,
因此AD⊥平面,又AD 平面,
故平面⊥平面;
(2)由(1)得是与侧面所成角,即,令,所以,又,
所以,,则,。
以A为原点,以,,分别为x轴,y轴,z轴的正方向,建立如图所 x示空间直角坐标系,
则A(0,0,0),D(1,1,0),(0,2,2)。所以。
设是平面的一个法向量,
则即取
易知是平面的一个法向量,则
而平面与平面的夹角为锐角,
所以平面与平面的夹角的余弦值为。
20. (1),
(2)
【分析】(1)根据对数运算得,利用等比数列定义求通项公式,利用等差中项判断数列}为等差数列,建立方程求出公差,从而可得}的通项;
(2)利用错位相减法计算即可。
【详解】(1)∵,∴,则,所以{}为等比数列,又,得,所以,
由知{}是等差数列,且
∴,得∴
(2)因为,,所以,
所以
则
上面两式作差得
,
∴
21. (1)
(2)
【分析】(1)求出,令,解得c,再分别讨论,利用函数f(x)在处有极大值,从而得出答案;
(2)确定函数的单调性,即可求f(x)在区间[1,2]上的最小值。
【详解】(1)由题知,
由题意,,得或,
当时,在,在(,2)上
此时,f(x)在处有极小值,不符题意;
当时,在,在(2,6)上;
此时,f(x)在处有极大值,符合题意。
综上,。
(2) 令,得或,
由,则在上,在(,c)上
即f(x)在上单调递增,在(,c)上单调递减。
由题意,
当时,f(x)在区间[1,2]上单调递减,则,
当时,f(x)在区间(1,c)上单调递减,在(c,2)上单调递增,则,
当时,f(x)在区间[1,2]上单调递增,则,
综上,
22. (1)
(2)(-1,)
【分析】(1)根据题意,列出方程组求得,求导,利用导数判断f(x)的单调性与极值;
(2)由题意得到原题意等价于与有三个交点,结合(1)中f(x)的单调性与极值,列式求解。
【详解】(1)∵
由题意得,解得,
所以,
令,解得或;令,解得
则上单调递增,在(-1,)上单调递减,
∴f(x)在处取到极大值,在处取到极小值,
故符合题意,
(2) 令,则,
原题意等价于与有三个交点,
由(1)可得:上单调递增,在(-1,)上单调递减,
∴f(x)在处取到极大值,在处取到极小值,
故,解得
所以m的取值范围为
同课章节目录
