第五章一元函数的导数及其应用 期中复习第二课时 课件(共17张PPT)
文档属性
| 名称 | 第五章一元函数的导数及其应用 期中复习第二课时 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
q期中复习选择性必修二第五章导数的应用
学习目标
主题一
主题二
主题三
主题四
授课过程
课堂小结
课堂练习
1.会求含参数的函数的最值.
2.掌握利用导数证明不等式的方法.
3.会利用导数解决不等式中的恒成立问题.
4.会用导数解决一些实际问题.
5.通过研究函数最值的应用,增强直观想象、逻辑推理与运算求解的数学素养.
学习目标:
【方法指导】:
(1)证明f(x)(2)证明f(x)>g(x),x∈(a,b),可以构造函数F(x)=f(x)-g(x),利用F(x)的单调性求最小值,证明F(x)min>0.
例1.证明不等式:ex≥1+x.
证明:设函数f(x)=ex-1-x,则f'(x)=ex-1.
令f'(x)=0,得x=0.
当x>0时,f'(x)>0,函数f(x)在区间(0,+∞)上单调递增;
当x<0时,f'(x)<0,函数f(x)在区间(-∞,0)上单调递减.
所以函数f(x)在x=0处取得极小值,也是最小值.
故f(x)≥f(0)=0,从而ex≥1+x.
主题1 利用导数证明不等式的方法础预习初探
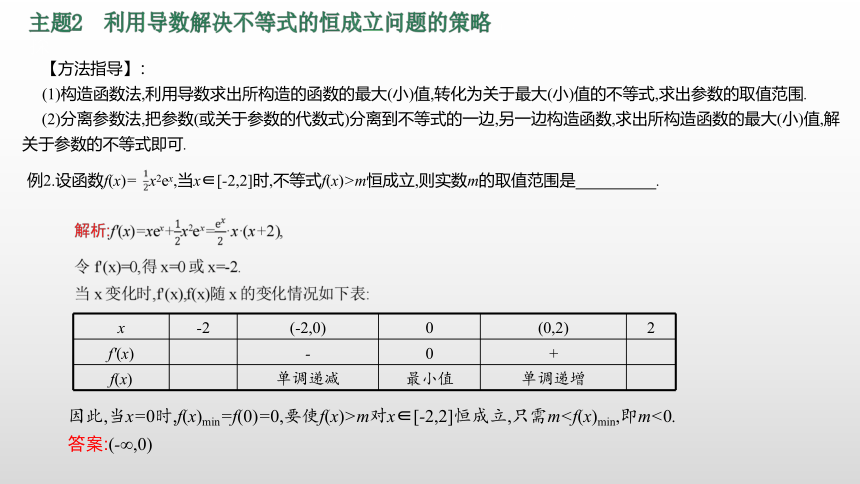
主题2 利用导数解决不等式的恒成立问题的策略础预习初探
【方法指导】:
(1)构造函数法,利用导数求出所构造的函数的最大(小)值,转化为关于最大(小)值的不等式,求出参数的取值范围.
(2)分离参数法,把参数(或关于参数的代数式)分离到不等式的一边,另一边构造函数,求出所构造函数的最大(小)值,解关于参数的不等式即可.
例2.设函数f(x)= x2ex,当x∈[-2,2]时,不等式f(x)>m恒成立,则实数m的取值范围是 .
x -2 (-2,0) 0 (0,2) 2
f'(x) - 0 +
f(x) 单调递减 最小值 单调递增
因此,当x=0时,f(x)min=f(0)=0,要使f(x)>m对x∈[-2,2]恒成立,只需m答案:(-∞,0)
主题3 解决实际问题础预习初探
例3.(1)要做一个圆锥形漏斗,其母线长为20 cm,若使其体积最大,则高应为( )
(2)用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2∶1,则该长方体的最大体积是 .
解析:(1)设高为h,0令V'=0,得x=0(舍去)或x=1.
根据V的单调性,可知V在x=1处取得极大值也是最大值.
故当该长方体的长、宽、高分别为2 m,1 m,1.5 m时,体积最大,最大体积 Vmax=3 m3.
答案:(1)A (2)3 m3
例4.某商场销售某种商品的经验表明,该商品每日的销售量y(单位:kg)与销售价格x(单位:元/kg)满足关系式y= +10(x-6)2.其中3(1)求a的值;
(2)若该商品的成本为3元/kg,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
从而f'(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6).
令f'(x)=0,得x=4或x=6(舍去).
当x变化时,f'(x),f(x)的变化情况如下表:
x (3,4) 4 (4,6)
f'(x) + 0 -
f(x) 单调递增 极大值42 单调递减
由上表可知,x=4是函数f(x)在区间(3,6)上的极大值点,也是最大值点.
所以当x=4时,函数f(x)取得最大值,且最大值等于42.
故当销售价格为4元/kg时,商场每日销售该商品所获得的利润最大.
例4.已知f(x)=x+ , g(x)=x+ln x,其中a>0.
(1)若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,求实数a的取值范围;
(2)若存在x1,x2∈[1,e],使得f(x1)分析:(1)“对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立”即为当x∈[1,e]时,函数f(x)的最小值不小于g(x)的最大值;
(2)“存在x1,x2∈[1,e],使得f(x1)主题4 两个函数中的存在性、任意性问题
础预习初探
解:(1)对 x1,x2∈[1,e],都有f(x1)≥g(x2),等价于当x∈[1,e]时,f(x)min≥g(x)max.
(2)存在x1,x2∈[1,e],使得f(x1)当x∈[1,e]时,g'(x)=1+ >0,
所以g(x)在区间[1,e]上单调递增,所以g(x)max=g(e)=e+1.
令f'(x)=0,解得x=a或x=-a(舍去),可得f(x)在区间(0,a)上单调递减,在区间(a,+∞)上单调递增.
当0当1≤a≤e时,f(x)在区间[1,a)上单调递减,在区间(a,e]上单调递增, f(x)min=f(a)=2a.
【变式训练】 已知函数f(x)=(x2-ax)ex,其函数图象在点(1,f(1))处的切线与x轴平行.
(1)讨论方程f(x)=m(m∈R)根的个数;
(2)设g(x)=b ,若对于任意的x1∈(0,2),总存在x2∈[1,e],使得f(x1)≥g(x2)成立,求实数b的取值范围.
解:(1)f'(x)=(2x-a)ex+(x2-ax)ex=[x2+(2-a)x-a]ex.
当x变化时,f'(x),f(x)的变化情况如下表:
且当x→-∞时,f(x)→0;当x→+∞时,f(x)→+∞.
作出函数f(x)的大致图象(图略),方程f(x)=m根的个数为函数y=f(x)的图象与直线y=m的交点个数.
(2)由题意知,只需f(x)min≥g(x)min,
当b>0时,g'(x)≥0,且不恒等于0,g(x)在区间[1,e]上单调递增,g(x)min=g(1)=b.
当b=0时,g(x)=0,无解.
当b<0时,g'(x)≤0,且不恒等于0,g(x)在区间[1,e]上单调递减,
因为a≤1,x∈[1,e],所以f'(x)≥0,所以函数f(x)在区间[1,e]上单调递增,从而f(x)min=f(1)=ln 1+a=a.故选B.
答案:B
课堂练习
解析:f'(x)=2x3-6x2=2x2(x-3),令f'(x)=0,解得x=0或x=3.
由函数f(x)的单调性,结合函数的图象可得x=3是函数的最小值点.
答案:A
课堂小结
1、证明不等式的策略.
2、恒成立问题的策略.
3、解决应用题的策略.
4、存在性和任意性的区别.
祝同学们学习进步!
谢谢同学们!同学们下课!
q期中复习选择性必修二第五章导数的应用
学习目标
主题一
主题二
主题三
主题四
授课过程
课堂小结
课堂练习
1.会求含参数的函数的最值.
2.掌握利用导数证明不等式的方法.
3.会利用导数解决不等式中的恒成立问题.
4.会用导数解决一些实际问题.
5.通过研究函数最值的应用,增强直观想象、逻辑推理与运算求解的数学素养.
学习目标:
【方法指导】:
(1)证明f(x)
例1.证明不等式:ex≥1+x.
证明:设函数f(x)=ex-1-x,则f'(x)=ex-1.
令f'(x)=0,得x=0.
当x>0时,f'(x)>0,函数f(x)在区间(0,+∞)上单调递增;
当x<0时,f'(x)<0,函数f(x)在区间(-∞,0)上单调递减.
所以函数f(x)在x=0处取得极小值,也是最小值.
故f(x)≥f(0)=0,从而ex≥1+x.
主题1 利用导数证明不等式的方法础预习初探
主题2 利用导数解决不等式的恒成立问题的策略础预习初探
【方法指导】:
(1)构造函数法,利用导数求出所构造的函数的最大(小)值,转化为关于最大(小)值的不等式,求出参数的取值范围.
(2)分离参数法,把参数(或关于参数的代数式)分离到不等式的一边,另一边构造函数,求出所构造函数的最大(小)值,解关于参数的不等式即可.
例2.设函数f(x)= x2ex,当x∈[-2,2]时,不等式f(x)>m恒成立,则实数m的取值范围是 .
x -2 (-2,0) 0 (0,2) 2
f'(x) - 0 +
f(x) 单调递减 最小值 单调递增
因此,当x=0时,f(x)min=f(0)=0,要使f(x)>m对x∈[-2,2]恒成立,只需m
主题3 解决实际问题础预习初探
例3.(1)要做一个圆锥形漏斗,其母线长为20 cm,若使其体积最大,则高应为( )
(2)用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2∶1,则该长方体的最大体积是 .
解析:(1)设高为h,0
根据V的单调性,可知V在x=1处取得极大值也是最大值.
故当该长方体的长、宽、高分别为2 m,1 m,1.5 m时,体积最大,最大体积 Vmax=3 m3.
答案:(1)A (2)3 m3
例4.某商场销售某种商品的经验表明,该商品每日的销售量y(单位:kg)与销售价格x(单位:元/kg)满足关系式y= +10(x-6)2.其中3
(2)若该商品的成本为3元/kg,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
从而f'(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6).
令f'(x)=0,得x=4或x=6(舍去).
当x变化时,f'(x),f(x)的变化情况如下表:
x (3,4) 4 (4,6)
f'(x) + 0 -
f(x) 单调递增 极大值42 单调递减
由上表可知,x=4是函数f(x)在区间(3,6)上的极大值点,也是最大值点.
所以当x=4时,函数f(x)取得最大值,且最大值等于42.
故当销售价格为4元/kg时,商场每日销售该商品所获得的利润最大.
例4.已知f(x)=x+ , g(x)=x+ln x,其中a>0.
(1)若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,求实数a的取值范围;
(2)若存在x1,x2∈[1,e],使得f(x1)
(2)“存在x1,x2∈[1,e],使得f(x1)
础预习初探
解:(1)对 x1,x2∈[1,e],都有f(x1)≥g(x2),等价于当x∈[1,e]时,f(x)min≥g(x)max.
(2)存在x1,x2∈[1,e],使得f(x1)
所以g(x)在区间[1,e]上单调递增,所以g(x)max=g(e)=e+1.
令f'(x)=0,解得x=a或x=-a(舍去),可得f(x)在区间(0,a)上单调递减,在区间(a,+∞)上单调递增.
当0
【变式训练】 已知函数f(x)=(x2-ax)ex,其函数图象在点(1,f(1))处的切线与x轴平行.
(1)讨论方程f(x)=m(m∈R)根的个数;
(2)设g(x)=b ,若对于任意的x1∈(0,2),总存在x2∈[1,e],使得f(x1)≥g(x2)成立,求实数b的取值范围.
解:(1)f'(x)=(2x-a)ex+(x2-ax)ex=[x2+(2-a)x-a]ex.
当x变化时,f'(x),f(x)的变化情况如下表:
且当x→-∞时,f(x)→0;当x→+∞时,f(x)→+∞.
作出函数f(x)的大致图象(图略),方程f(x)=m根的个数为函数y=f(x)的图象与直线y=m的交点个数.
(2)由题意知,只需f(x)min≥g(x)min,
当b>0时,g'(x)≥0,且不恒等于0,g(x)在区间[1,e]上单调递增,g(x)min=g(1)=b.
当b=0时,g(x)=0,无解.
当b<0时,g'(x)≤0,且不恒等于0,g(x)在区间[1,e]上单调递减,
因为a≤1,x∈[1,e],所以f'(x)≥0,所以函数f(x)在区间[1,e]上单调递增,从而f(x)min=f(1)=ln 1+a=a.故选B.
答案:B
课堂练习
解析:f'(x)=2x3-6x2=2x2(x-3),令f'(x)=0,解得x=0或x=3.
由函数f(x)的单调性,结合函数的图象可得x=3是函数的最小值点.
答案:A
课堂小结
1、证明不等式的策略.
2、恒成立问题的策略.
3、解决应用题的策略.
4、存在性和任意性的区别.
祝同学们学习进步!
谢谢同学们!同学们下课!
