第十八章 平行四边形单元测试题(含答案)
文档属性
| 名称 | 第十八章 平行四边形单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 300.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 14:09:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A.4.5 B.9 C.10 D.12
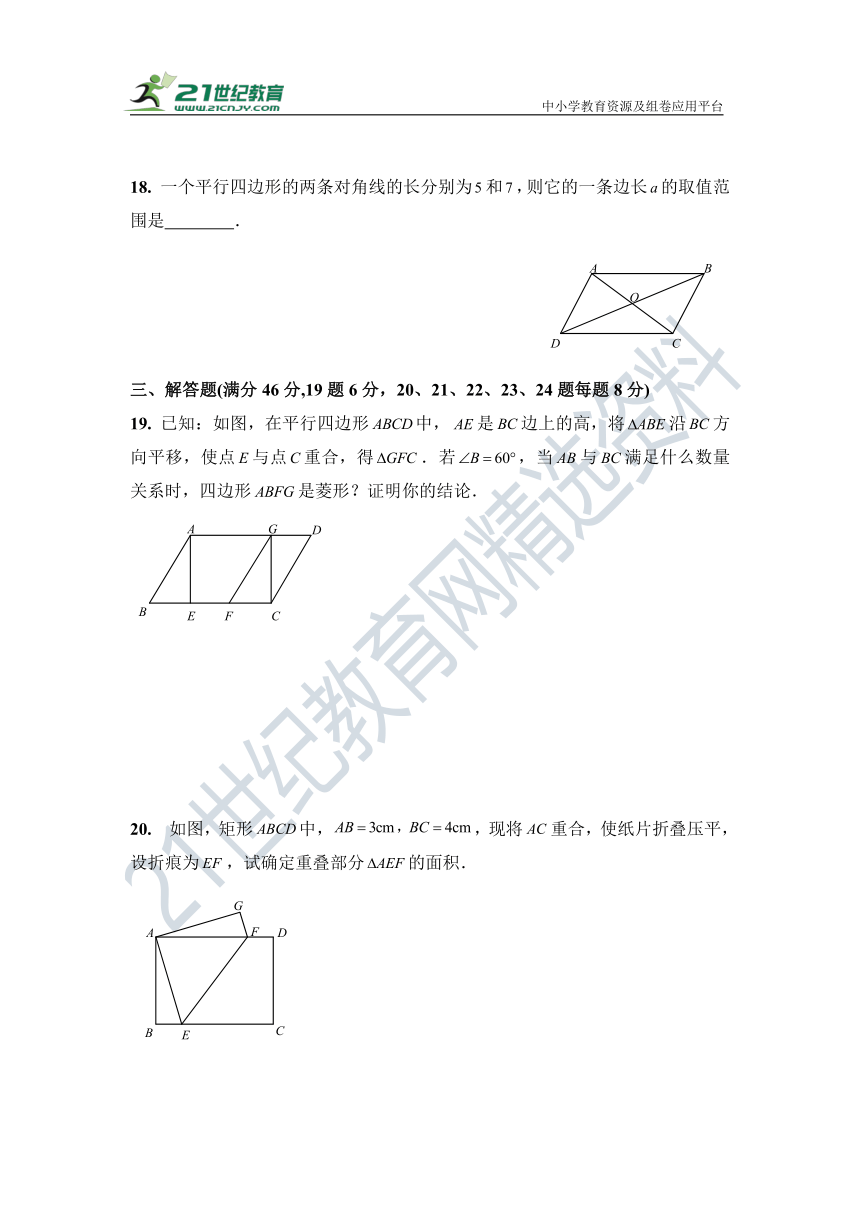
2.平行四边形ABCD中,对角线AC和BD相交于点O,若AC=3,AB=6,BD=m,那么m的取值范围是( )
A.9<m<15 B.2<m<14 C.6<m<8 D.4<m<20
3.如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360° B.540° C.630° D.720°
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8,如图4,菱形花坛 ABCD的边长为 6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )
A.12m B.20m C.22m D.24m
9.下列命题是假命题的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直且平分的四边形是正方形
10. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠2=40°,则图中∠1的度数为( )
A. 115° B. 120° C. 130° D. 140°
二、填空题(每题3分,共30分)
11.在平行四边形ABCD中,∠B+∠D=100°,则∠A等于________度.
12.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,OE=6cm,则AD的长是_____cm.
13.如图,直角三角形ABC中,AC=1,BC=2,P为斜边AB上一动点.PE⊥BC,PF⊥CA,则线段EF长的最小值为________.
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
18. 一个平行四边形的两条对角线的长分别为和,则它的一条边长的取值范围是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 已知:如图,在平行四边形中,是边上的高,将沿方向平移,使点与点重合,得.若,当与满足什么数量关系时,四边形是菱形?证明你的结论.
20. 如图,矩形中,,现将重合,使纸片折叠压平,设折痕为,试确定重叠部分的面积.
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
24.如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并延长交AB的延长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C D D D B D C
二、填空题(每题3分,共24分)
11.130;. 解析:∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,∴∠A+∠D=180°,
∵∠B+∠D=100°,∴∠B=∠D=50°,
∴∠A =180°-∠D=130°,故答案为:130.
12.12. 解析:∵四边形ABCD是平行四边形,∴BO=DO,
又∵点E是AB的中点,∴OE=AD,
∵OE=6cm,∴AD=12cm,故答案为12
13.. 解析:连接PC,
∵PE⊥BC, PF⊥CA, ∴∠PEC=∠PFC=∠C=90°,
∴四边形ECFP是矩形, ∴EF=PC, ∴当PC最小时, EF也最小,
∵垂线段最短, ∴当CP⊥AB时,PC最小,
∵AC=1, BC=2, ∴AB=,又∵当CP⊥AB时
,
PC===.
∴线段EF长的最小值为. 故答案为.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17. 【答案】4.8 【解析】∵S菱形=AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=4,BO=BD=3,∴在Rt△AOB中,AB==5,∴DH==4.8.
18. 【答案】
【解析】如图,不妨设,,,在中,
,,由三角形三边关系可得
,即.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 【答案】
当时,四边形是菱形.
∵,
∴四边形是平行四边形
∵中,
∴
∴
∵,
∴
∴
∴四边形是菱形.
20. 【答案】
【解析】
如图,连结,因折叠后重合,
所以,
∵,∴
∴
又
得,于是可得
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
【分析】(1)根据全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的性质得到:EH=GF,同理可得FE=HG,即可得四边形EFGH是平行四边形;
(3)由 轴对称﹣﹣最短路径问题得到:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
证明:(1)∵四边形ABCD是矩形,
∴∠A=∠C.
∴在△AEH与△CGF中,,
∴△AEH≌△CGF(SAS);
(2)四边形EFGH是平行四边形,理由如下:
∵由(1)知,△AEH≌△CGF,则EH=GF,同理证得△EBF≌△GDH,则EF=GH,
∴四边形EFGH是平行四边形;
(3)四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.
连接AC,
∵CG′=CG=AE,AB∥CG′,
∴四边形AEG′C为平行四边形,
∴EG′=AC.
在△EFG′中,∵EF+FG′>EG′=AC,
∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
24.如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并延长交AB的延长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
【分析】(1)根据作线段的垂直平分线的方法作图即可得出结论;
(2)先求出DE=CE=1,进而判断出△ADE≌△BCE,得出∠AED=∠BEC,再求出∠AED,即可得出结论;
(3)先判断出△AEP≌△FBP,即可得出结论.
解:(1)依题意作出图形如图①所示,
(2)EB是平分∠AEC,理由:
∵四边形ABCD是矩形,
∴∠C=∠D=90°,CD=AB=2,BC=AD=,
∵点E是CD的中点,
∴DE=CE=CD=1,
在△ADE和△BCE中,,
∴△ADE≌△BCE(SAS),
∴∠AED=∠BEC,
在Rt△ADE中,AD=,DE=1,
∴∠AED=60°,
∴∠BEC=∠AED=60°
∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,
∴BE平分∠AEC;
(3)∵BP=2CP,BC=,
∴CP=,BP=,
∴∠CEP=30°,
∴∠BEP=30°,
∴∠AEP=90°,
∵CD∥AB,
∴∠F=∠CEP=30°,
∴∠PAB=30°,
∴∠EAP=30°=∠F=∠PAB,
∵CB⊥AF,
∴AP=FP,
∴△AEP≌△FBP,
∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形,
变换的方法为:①将△BPF绕点P顺时针旋转120°和△EPA重合,再沿PE折叠,
②将△BPF以过点P垂直于BC的直线折叠,再绕点P逆时针旋转60°.
图4
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A.4.5 B.9 C.10 D.12
2.平行四边形ABCD中,对角线AC和BD相交于点O,若AC=3,AB=6,BD=m,那么m的取值范围是( )
A.9<m<15 B.2<m<14 C.6<m<8 D.4<m<20
3.如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360° B.540° C.630° D.720°
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8,如图4,菱形花坛 ABCD的边长为 6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )
A.12m B.20m C.22m D.24m
9.下列命题是假命题的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直且平分的四边形是正方形
10. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠2=40°,则图中∠1的度数为( )
A. 115° B. 120° C. 130° D. 140°
二、填空题(每题3分,共30分)
11.在平行四边形ABCD中,∠B+∠D=100°,则∠A等于________度.
12.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,OE=6cm,则AD的长是_____cm.
13.如图,直角三角形ABC中,AC=1,BC=2,P为斜边AB上一动点.PE⊥BC,PF⊥CA,则线段EF长的最小值为________.
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
18. 一个平行四边形的两条对角线的长分别为和,则它的一条边长的取值范围是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 已知:如图,在平行四边形中,是边上的高,将沿方向平移,使点与点重合,得.若,当与满足什么数量关系时,四边形是菱形?证明你的结论.
20. 如图,矩形中,,现将重合,使纸片折叠压平,设折痕为,试确定重叠部分的面积.
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
24.如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并延长交AB的延长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C D D D B D C
二、填空题(每题3分,共24分)
11.130;. 解析:∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,∴∠A+∠D=180°,
∵∠B+∠D=100°,∴∠B=∠D=50°,
∴∠A =180°-∠D=130°,故答案为:130.
12.12. 解析:∵四边形ABCD是平行四边形,∴BO=DO,
又∵点E是AB的中点,∴OE=AD,
∵OE=6cm,∴AD=12cm,故答案为12
13.. 解析:连接PC,
∵PE⊥BC, PF⊥CA, ∴∠PEC=∠PFC=∠C=90°,
∴四边形ECFP是矩形, ∴EF=PC, ∴当PC最小时, EF也最小,
∵垂线段最短, ∴当CP⊥AB时,PC最小,
∵AC=1, BC=2, ∴AB=,又∵当CP⊥AB时
,
PC===.
∴线段EF长的最小值为. 故答案为.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17. 【答案】4.8 【解析】∵S菱形=AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=4,BO=BD=3,∴在Rt△AOB中,AB==5,∴DH==4.8.
18. 【答案】
【解析】如图,不妨设,,,在中,
,,由三角形三边关系可得
,即.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 【答案】
当时,四边形是菱形.
∵,
∴四边形是平行四边形
∵中,
∴
∴
∵,
∴
∴
∴四边形是菱形.
20. 【答案】
【解析】
如图,连结,因折叠后重合,
所以,
∵,∴
∴
又
得,于是可得
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23.如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
【分析】(1)根据全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的性质得到:EH=GF,同理可得FE=HG,即可得四边形EFGH是平行四边形;
(3)由 轴对称﹣﹣最短路径问题得到:四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
证明:(1)∵四边形ABCD是矩形,
∴∠A=∠C.
∴在△AEH与△CGF中,,
∴△AEH≌△CGF(SAS);
(2)四边形EFGH是平行四边形,理由如下:
∵由(1)知,△AEH≌△CGF,则EH=GF,同理证得△EBF≌△GDH,则EF=GH,
∴四边形EFGH是平行四边形;
(3)四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
理由如下:作G关于BC的对称点G′,连接EG′,可得EG′的长度就是EF+FG的最小值.
连接AC,
∵CG′=CG=AE,AB∥CG′,
∴四边形AEG′C为平行四边形,
∴EG′=AC.
在△EFG′中,∵EF+FG′>EG′=AC,
∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度.
24.如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并延长交AB的延长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
【分析】(1)根据作线段的垂直平分线的方法作图即可得出结论;
(2)先求出DE=CE=1,进而判断出△ADE≌△BCE,得出∠AED=∠BEC,再求出∠AED,即可得出结论;
(3)先判断出△AEP≌△FBP,即可得出结论.
解:(1)依题意作出图形如图①所示,
(2)EB是平分∠AEC,理由:
∵四边形ABCD是矩形,
∴∠C=∠D=90°,CD=AB=2,BC=AD=,
∵点E是CD的中点,
∴DE=CE=CD=1,
在△ADE和△BCE中,,
∴△ADE≌△BCE(SAS),
∴∠AED=∠BEC,
在Rt△ADE中,AD=,DE=1,
∴∠AED=60°,
∴∠BEC=∠AED=60°
∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,
∴BE平分∠AEC;
(3)∵BP=2CP,BC=,
∴CP=,BP=,
∴∠CEP=30°,
∴∠BEP=30°,
∴∠AEP=90°,
∵CD∥AB,
∴∠F=∠CEP=30°,
∴∠PAB=30°,
∴∠EAP=30°=∠F=∠PAB,
∵CB⊥AF,
∴AP=FP,
∴△AEP≌△FBP,
∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形,
变换的方法为:①将△BPF绕点P顺时针旋转120°和△EPA重合,再沿PE折叠,
②将△BPF以过点P垂直于BC的直线折叠,再绕点P逆时针旋转60°.
图4
