1.3 探索三角形全等的条件(3) 导学案
文档属性
| 名称 | 1.3 探索三角形全等的条件(3) 导学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 369.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 19:02:38 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.3探索三角形全等的条件(3)
【学习目标】
1.经历探索判定三角形全等“边角边”条件的过程;
2.掌握并能应用“边角边”条件说明两个三角形全等.
【课前梳理】
预习课本24-25页,思考并完成下列问题.
1.想一想: 如果已知一个三角形的两边及一角,有 种可能的情况呢,每种情况下得到的三角形都全等吗?
2.本节课学到的判定三角形全等的方法为
【课堂练习】
知识点 用“SAS”判定三角形全等
1.已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,AB=CD.那么△ABE与△CDF全等吗?为什么?
2.下列条件,不能判定两个三角形全等的是( )
A.两边及一角对应相等 B.两角及其中一角的对边对应相等
C.三边对应相等 D.两边及其夹角对应相等
【当堂达标】
1.如图,已知AO=DO,BO=CO,说明:∠ABD=∠DCA.
2.已知AB=AC,AD=AE,∠1=∠2,BE与CD相等吗?为什么?
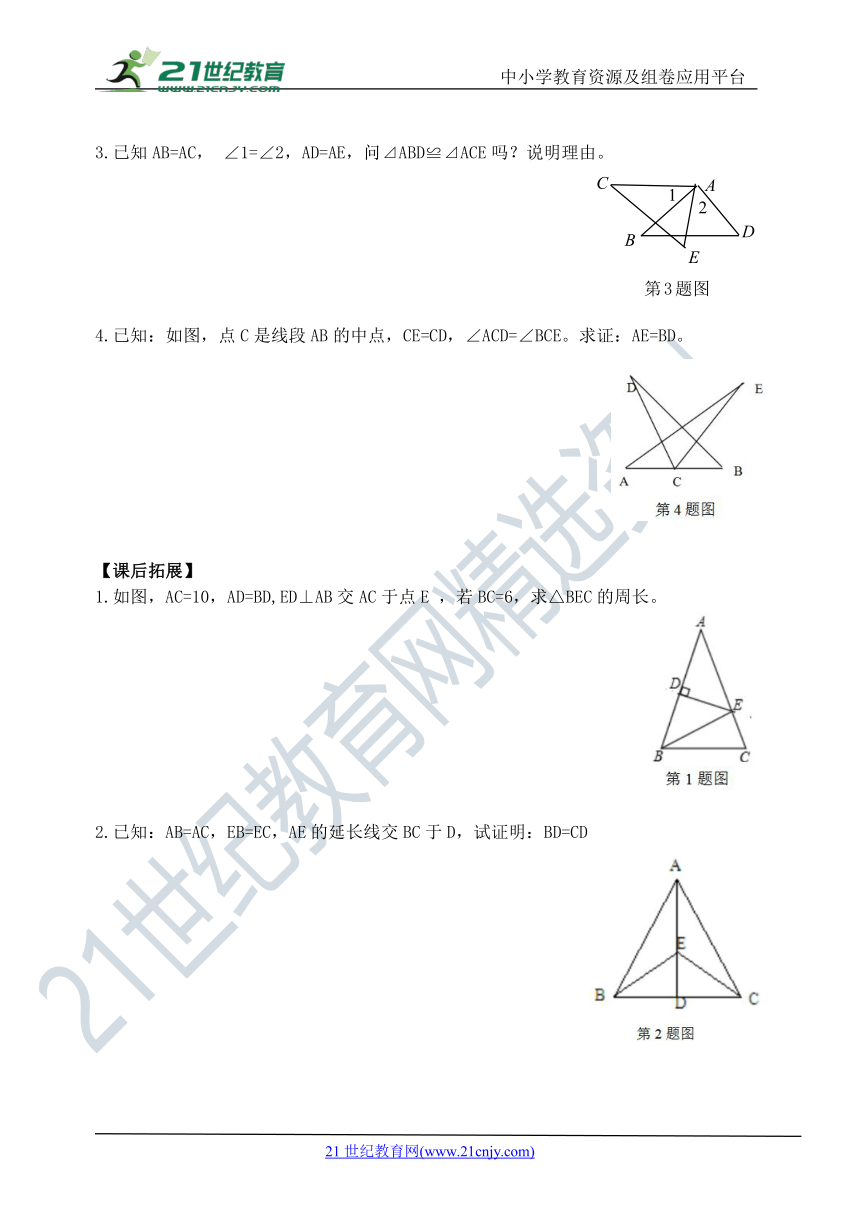
3.已知AB=AC, ∠1=∠2,AD=AE,问⊿ABD≌⊿ACE吗?说明理由。
4.已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE。求证:AE=BD。
【课后拓展】
1.如图,AC=10,AD=BD,ED⊥AB交AC于点E ,若BC=6,求△BEC的周长。
2.已知:AB=AC,EB=EC,AE的延长线交BC于D,试证明:BD=CD
1.3探索三角形全等的条件(3)
【课堂练习】
1. ∵AF=CE,
∴AF+EF=CE+EF,
∴AE=CF,
∵BE∥DF,
∴∠AEB=∠CFD
在△ABE和△CDF中
AB=CD
∠AEB=∠CFD
AE=CF,
∴△ABE≌△CDF (SAS).
2.A
【当堂达标】
略
2.解:因为∠1=∠2
所以∠1+∠BAC=∠BAC+∠2 即∠DAC=∠EAB.
∵在△ACD与△ABE中,AC=AB,∠DAC=∠EAB, AD=AE,
∴△ACD≌△ABE(SAS),
∴BE=CD.
4.解:∵点C是线段AB的中点,
∴AC=BC,
∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD,
在△ACE和△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD.
【课后拓展】
1. 16
2.解:在△ABE和△ACE中,
,
∴△ABE≌△ACE(SSS),
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD.
第1题图
O
第1题图
A
D
B
E
C
1
2
第3题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
1.3探索三角形全等的条件(3)
【学习目标】
1.经历探索判定三角形全等“边角边”条件的过程;
2.掌握并能应用“边角边”条件说明两个三角形全等.
【课前梳理】
预习课本24-25页,思考并完成下列问题.
1.想一想: 如果已知一个三角形的两边及一角,有 种可能的情况呢,每种情况下得到的三角形都全等吗?
2.本节课学到的判定三角形全等的方法为
【课堂练习】
知识点 用“SAS”判定三角形全等
1.已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,AB=CD.那么△ABE与△CDF全等吗?为什么?
2.下列条件,不能判定两个三角形全等的是( )
A.两边及一角对应相等 B.两角及其中一角的对边对应相等
C.三边对应相等 D.两边及其夹角对应相等
【当堂达标】
1.如图,已知AO=DO,BO=CO,说明:∠ABD=∠DCA.
2.已知AB=AC,AD=AE,∠1=∠2,BE与CD相等吗?为什么?
3.已知AB=AC, ∠1=∠2,AD=AE,问⊿ABD≌⊿ACE吗?说明理由。
4.已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE。求证:AE=BD。
【课后拓展】
1.如图,AC=10,AD=BD,ED⊥AB交AC于点E ,若BC=6,求△BEC的周长。
2.已知:AB=AC,EB=EC,AE的延长线交BC于D,试证明:BD=CD
1.3探索三角形全等的条件(3)
【课堂练习】
1. ∵AF=CE,
∴AF+EF=CE+EF,
∴AE=CF,
∵BE∥DF,
∴∠AEB=∠CFD
在△ABE和△CDF中
AB=CD
∠AEB=∠CFD
AE=CF,
∴△ABE≌△CDF (SAS).
2.A
【当堂达标】
略
2.解:因为∠1=∠2
所以∠1+∠BAC=∠BAC+∠2 即∠DAC=∠EAB.
∵在△ACD与△ABE中,AC=AB,∠DAC=∠EAB, AD=AE,
∴△ACD≌△ABE(SAS),
∴BE=CD.
4.解:∵点C是线段AB的中点,
∴AC=BC,
∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD,
在△ACE和△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD.
【课后拓展】
1. 16
2.解:在△ABE和△ACE中,
,
∴△ABE≌△ACE(SSS),
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD.
第1题图
O
第1题图
A
D
B
E
C
1
2
第3题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
