第二章 轴对称复习学案
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 轴对称复习学案
【本章目标】
1.掌握对称轴的画法及条数的确定,体会轴对称在生活中的应用及其丰富的文化价值;
2.认识轴对称图形和两个图形成轴对称的概念,并理解轴对称图形的性质;
3.探索并了解基本图形的轴对称性及其相关性质.
【知识梳理】
1. 叫做轴对称图形
叫做对称轴.
2.如果
那么称这两个图形成轴对称, 叫做这两个图形的对称轴.
3.轴对称的性质;在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴
对应线段 ,对应角 .
4.线段的轴对称性:线段是________图形,线段的__________是它的对称轴;线段的垂直平分线上的点到________________相等.
5.角的轴对称性:角是 图形,它的对称轴是 ;角平分线上的点到____________________相等.
6.等腰三角形的轴对称性:等腰三角形是 图形,等腰三角形的两个______相等,等腰三角形的 平分线、 上的高和 上的中线互相重合(简称“三线合一”) 等腰三角形的判定方法:(1)定义:有 相等的三角形,叫做等腰三角形.
(2)判定: .
7.等边三角形的轴对称性:等边三角形是____________图形,并且有____条对称轴.
等边三角形的每个内角都等于________.
等边三角形的判定方法:(1)定义:有 相等的三角形,叫做等边三角形.(2)判定方法1:三个角都相等的三角形是 三角形;判定方法2:有一个角等于600 的等腰三角形是 三角形.
应用:在直角三角形中,如果一个锐角 ,那么 的一半.
【典型例题】
考点一 轴对称图形
例1.下列图形中对称轴最多的是( )
A.等腰三角形 B.正方形 C.圆 D.线段
巩固训练1
下列图案是几种名车的标志,在这几个图案中不是轴对称图形的是( )
A. B. C. D.
考点二 轴对称的性质
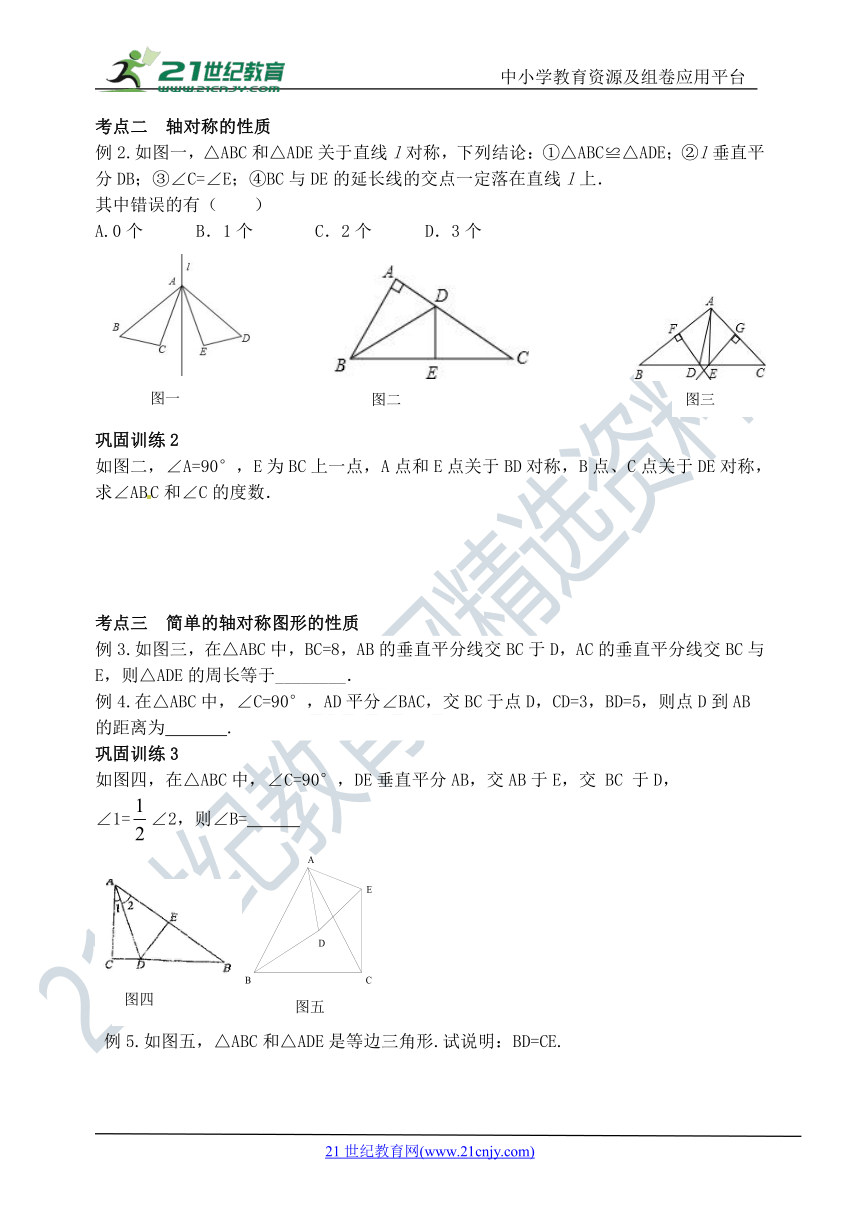
例2.如图一,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.
其中错误的有( )
A.0个 B.1个 C.2个 D.3个
巩固训练2
如图二,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
考点三 简单的轴对称图形的性质
例3.如图三,在△ABC中,BC=8,AB的垂直平分线交BC于D,AC的垂直平分线交BC与E,则△ADE的周长等于________.
例4.在△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=3,BD=5,则点D到AB的距离为 .
巩固训练3
如图四,在△ABC中,∠C=90°,DE垂直平分AB,交AB于E,交 BC 于D,
∠1=∠2,则∠B=
例5.如图五,△ABC和△ADE是等边三角形.试说明:BD=CE.
巩固训练4.
如图六,△ABC和△ADE是等边三角形,AD是BC边上的中线。求证:BE=BD。
【达标测试】
一.选择题
1.下列轴对称图形中,对称轴条数最少的是( )
A.等腰直角三角形 B.正方形 C.等边三角形 D.长方形
2.在下列说法中,正确的是( )
A.如果两个三角形全等,则它们必是关于直线成轴对称的图形
B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于底边中线成轴对称的图形
D.一条线段是关于经过该线段中点的直线成轴对称的图形
3.已知直角三角形中30°角所对的直角边为2㎝,则斜边的长为( )
A.2 ㎝ B.4 ㎝ C.6 ㎝ D.8㎝
4.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
A.11cm B.7.5cm C.11cm或7.5cm D.以上都不对
5.∠AOB的平分线上一点P到OA的距离为5,Q是OB上任一点,则 ( )
A.PQ>5 B.PQ≥5 C.PQ<5 D.PQ≤5
二.填空题
6.角是轴对称图形,其对称轴是________________________.
7.等腰三角形一个底角是30°,则它的顶角是__________度;
8.已知线段AB的端点B在直线 上(AB与 不垂直)请在直线 上另找一点C,使三角形ABC是等腰三角形,这样的点能找 个。
三.解答题
9.如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.
试说明:AB=AC.
10.△ABC中,∠B=90°,AC的垂直平分线交AC于D,交BC于E,又∠C=15°,EC=1求AB的长。
11.如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M, 试说明:(1)BD平分∠ABC (2)△BCD为等腰三角形.
12.如图所示,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、AC延长线于点F、E.试说明:DF∥AC
13.如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.试说明△BDE是等腰三角形.
14.如图,∠B=∠C=90°,AE平分∠BAD,DE平分∠CDA,且AE与DE交BC于E.试说明:(1)BE=CE (2)AE⊥DE
七年级数学第二章轴对称复习学案参考答案
【典型例题】
例1.C 巩固训练1.A 例2.A 巩固训练2. ∠ABC=60° ∠C=30°
例3. 8 例4. 3 巩固训练3 . 36°
【达标测试】
1-5 ABCCB 6.角平分线所在的直线 7.120° 8.四
9. 解:∵BD=CE,∠DBC=∠ECB,BC=CB,
∴△BCE≌△CBD.
∴∠ACB=∠ABC.
∴AB=AC.
10.0.5
12..解:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC.
13.∵DE∥AC,
∴∠1=∠3,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠2=∠3,
∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°,
∴∠B=∠BDE,
∴BE=DE,
∴△BDE是等腰三角形.
14.(1)过E作EF⊥AD,
∵∠B=∠C=90°,AE平分∠BAD,DE平分∠CDA,
∴EF=CE,EF=EB,
∴CE=EB;
(2)∵∠B=∠C=90°,AE平分∠BAD,DE平分∠CDA,
∴∠CDE=∠FDE,∠FAE=∠BAE,
在△EFD与△ECD中
,
∴△EFD≌△ECD(AAS),
∴∠CED=∠FED,
同理可得:∠FEA=∠BEA,
∵∠CED+∠FED+∠FEA+∠BEA=180°,
∴∠DEA=90°,
∴DE⊥AE.
图一
图二
图三
图四
图五
图六
A
B
l
第8题图
第9题图
第11题图
第12题图
第13题图
第14题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二章 轴对称复习学案
【本章目标】
1.掌握对称轴的画法及条数的确定,体会轴对称在生活中的应用及其丰富的文化价值;
2.认识轴对称图形和两个图形成轴对称的概念,并理解轴对称图形的性质;
3.探索并了解基本图形的轴对称性及其相关性质.
【知识梳理】
1. 叫做轴对称图形
叫做对称轴.
2.如果
那么称这两个图形成轴对称, 叫做这两个图形的对称轴.
3.轴对称的性质;在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴
对应线段 ,对应角 .
4.线段的轴对称性:线段是________图形,线段的__________是它的对称轴;线段的垂直平分线上的点到________________相等.
5.角的轴对称性:角是 图形,它的对称轴是 ;角平分线上的点到____________________相等.
6.等腰三角形的轴对称性:等腰三角形是 图形,等腰三角形的两个______相等,等腰三角形的 平分线、 上的高和 上的中线互相重合(简称“三线合一”) 等腰三角形的判定方法:(1)定义:有 相等的三角形,叫做等腰三角形.
(2)判定: .
7.等边三角形的轴对称性:等边三角形是____________图形,并且有____条对称轴.
等边三角形的每个内角都等于________.
等边三角形的判定方法:(1)定义:有 相等的三角形,叫做等边三角形.(2)判定方法1:三个角都相等的三角形是 三角形;判定方法2:有一个角等于600 的等腰三角形是 三角形.
应用:在直角三角形中,如果一个锐角 ,那么 的一半.
【典型例题】
考点一 轴对称图形
例1.下列图形中对称轴最多的是( )
A.等腰三角形 B.正方形 C.圆 D.线段
巩固训练1
下列图案是几种名车的标志,在这几个图案中不是轴对称图形的是( )
A. B. C. D.
考点二 轴对称的性质
例2.如图一,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.
其中错误的有( )
A.0个 B.1个 C.2个 D.3个
巩固训练2
如图二,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
考点三 简单的轴对称图形的性质
例3.如图三,在△ABC中,BC=8,AB的垂直平分线交BC于D,AC的垂直平分线交BC与E,则△ADE的周长等于________.
例4.在△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=3,BD=5,则点D到AB的距离为 .
巩固训练3
如图四,在△ABC中,∠C=90°,DE垂直平分AB,交AB于E,交 BC 于D,
∠1=∠2,则∠B=
例5.如图五,△ABC和△ADE是等边三角形.试说明:BD=CE.
巩固训练4.
如图六,△ABC和△ADE是等边三角形,AD是BC边上的中线。求证:BE=BD。
【达标测试】
一.选择题
1.下列轴对称图形中,对称轴条数最少的是( )
A.等腰直角三角形 B.正方形 C.等边三角形 D.长方形
2.在下列说法中,正确的是( )
A.如果两个三角形全等,则它们必是关于直线成轴对称的图形
B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于底边中线成轴对称的图形
D.一条线段是关于经过该线段中点的直线成轴对称的图形
3.已知直角三角形中30°角所对的直角边为2㎝,则斜边的长为( )
A.2 ㎝ B.4 ㎝ C.6 ㎝ D.8㎝
4.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
A.11cm B.7.5cm C.11cm或7.5cm D.以上都不对
5.∠AOB的平分线上一点P到OA的距离为5,Q是OB上任一点,则 ( )
A.PQ>5 B.PQ≥5 C.PQ<5 D.PQ≤5
二.填空题
6.角是轴对称图形,其对称轴是________________________.
7.等腰三角形一个底角是30°,则它的顶角是__________度;
8.已知线段AB的端点B在直线 上(AB与 不垂直)请在直线 上另找一点C,使三角形ABC是等腰三角形,这样的点能找 个。
三.解答题
9.如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.
试说明:AB=AC.
10.△ABC中,∠B=90°,AC的垂直平分线交AC于D,交BC于E,又∠C=15°,EC=1求AB的长。
11.如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M, 试说明:(1)BD平分∠ABC (2)△BCD为等腰三角形.
12.如图所示,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、AC延长线于点F、E.试说明:DF∥AC
13.如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.试说明△BDE是等腰三角形.
14.如图,∠B=∠C=90°,AE平分∠BAD,DE平分∠CDA,且AE与DE交BC于E.试说明:(1)BE=CE (2)AE⊥DE
七年级数学第二章轴对称复习学案参考答案
【典型例题】
例1.C 巩固训练1.A 例2.A 巩固训练2. ∠ABC=60° ∠C=30°
例3. 8 例4. 3 巩固训练3 . 36°
【达标测试】
1-5 ABCCB 6.角平分线所在的直线 7.120° 8.四
9. 解:∵BD=CE,∠DBC=∠ECB,BC=CB,
∴△BCE≌△CBD.
∴∠ACB=∠ABC.
∴AB=AC.
10.0.5
12..解:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC.
13.∵DE∥AC,
∴∠1=∠3,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠2=∠3,
∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°,
∴∠B=∠BDE,
∴BE=DE,
∴△BDE是等腰三角形.
14.(1)过E作EF⊥AD,
∵∠B=∠C=90°,AE平分∠BAD,DE平分∠CDA,
∴EF=CE,EF=EB,
∴CE=EB;
(2)∵∠B=∠C=90°,AE平分∠BAD,DE平分∠CDA,
∴∠CDE=∠FDE,∠FAE=∠BAE,
在△EFD与△ECD中
,
∴△EFD≌△ECD(AAS),
∴∠CED=∠FED,
同理可得:∠FEA=∠BEA,
∵∠CED+∠FED+∠FEA+∠BEA=180°,
∴∠DEA=90°,
∴DE⊥AE.
图一
图二
图三
图四
图五
图六
A
B
l
第8题图
第9题图
第11题图
第12题图
第13题图
第14题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
