吉林省长春市2022-2023学年九年级下学期第二次月考数学试题(无答案)
文档属性
| 名称 | 吉林省长春市2022-2023学年九年级下学期第二次月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 470.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 18:23:30 | ||
图片预览

文档简介
吉林省2022-2023学年度下学期九年级第二次月考
数学试题
本试卷包括三道大题,共24小题。共6页。全卷满分120分。考试时间为120分钟。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,考生务必将自己的姓名、校区、准考证号填写在答题卡上,并将条形码准确粘贴在条形码区域内。
2.答题时,考生务必按照考试要求在答题卡上的指定区域内作答,在草稿纸、试卷上答题无效。
一、选择题(本大题共8小题,每小题3分,共24分)
1.在,,0,2四个数中,最大的数是( )
A. B.0 C.2 D.
2.据《人民网》报道,在2022卡塔尔世界杯承担开、闭幕式等重要活动的卢塞尔球场是由中国铁建集团承建,其建筑面积为195000平方米.把数字“195000”用科学记数法表示为( )
A. B. C. D.
3.如图是由6个大小相同的小正方体拼成的几何体,当去掉某一个小正方体时,与原几何体比较,则下列说法正确的是( )
A.去掉①,主视图不变 B.去掉②,俯视图不变
C.去掉③,左视图不变 D.去掉④,俯视图不变
4.不等式的解集在数轴上表示,正确的是( )
A. B.
C. D.
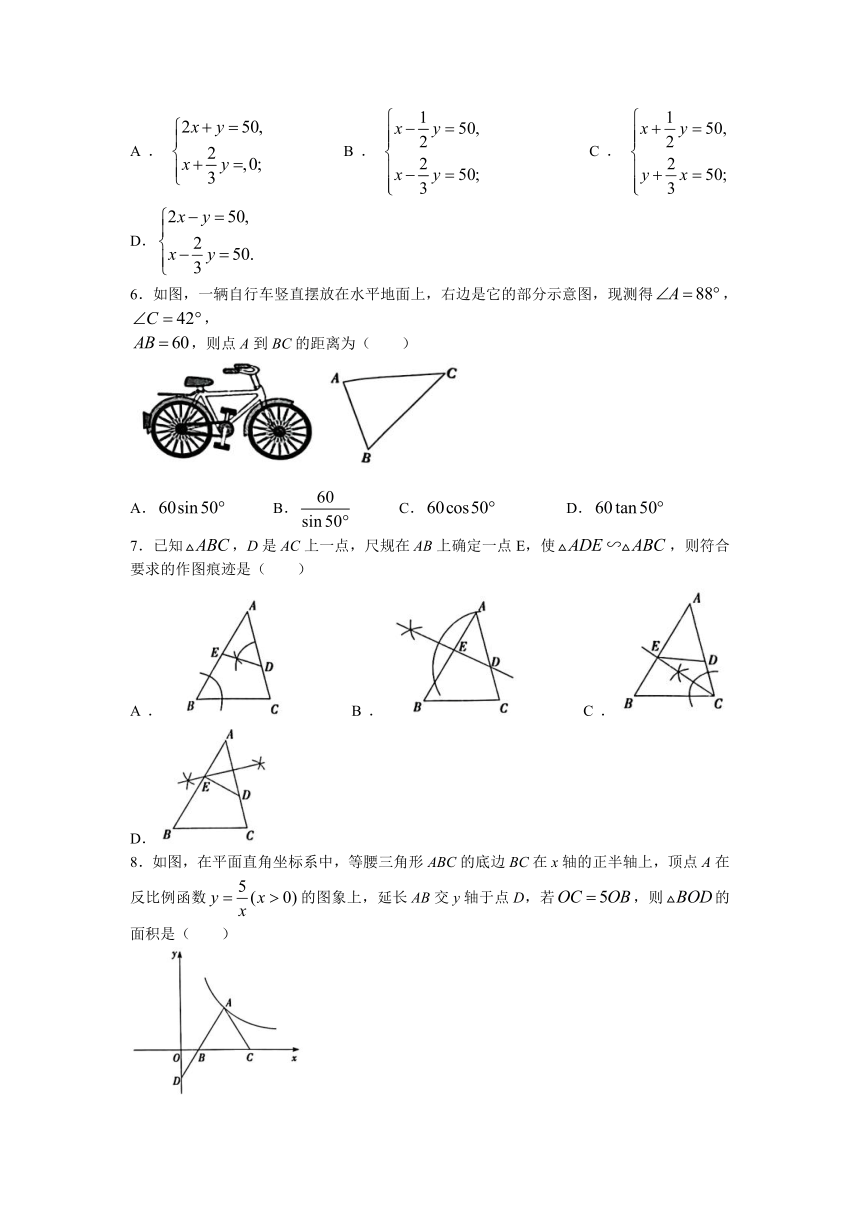
5.《九章算术》中记载了一个问题,大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的,那么乙也共有钱50.问:甲,乙两人各带了多少钱?设甲,乙两人持钱的数量分别为x,y,则可列方程组为( )
A. B. C. D.
6.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得,,
,则点A到BC的距离为( )
A. B. C. D.
7.已知,D是AC上一点,尺规在AB上确定一点E,使,则符合要求的作图痕迹是( )
A. B. C. D.
8.如图,在平面直角坐标系中,等腰三角形ABC的底边BC在x轴的正半轴上,顶点A在反比例函数的图象上,延长AB交y轴于点D,若,则的面积是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
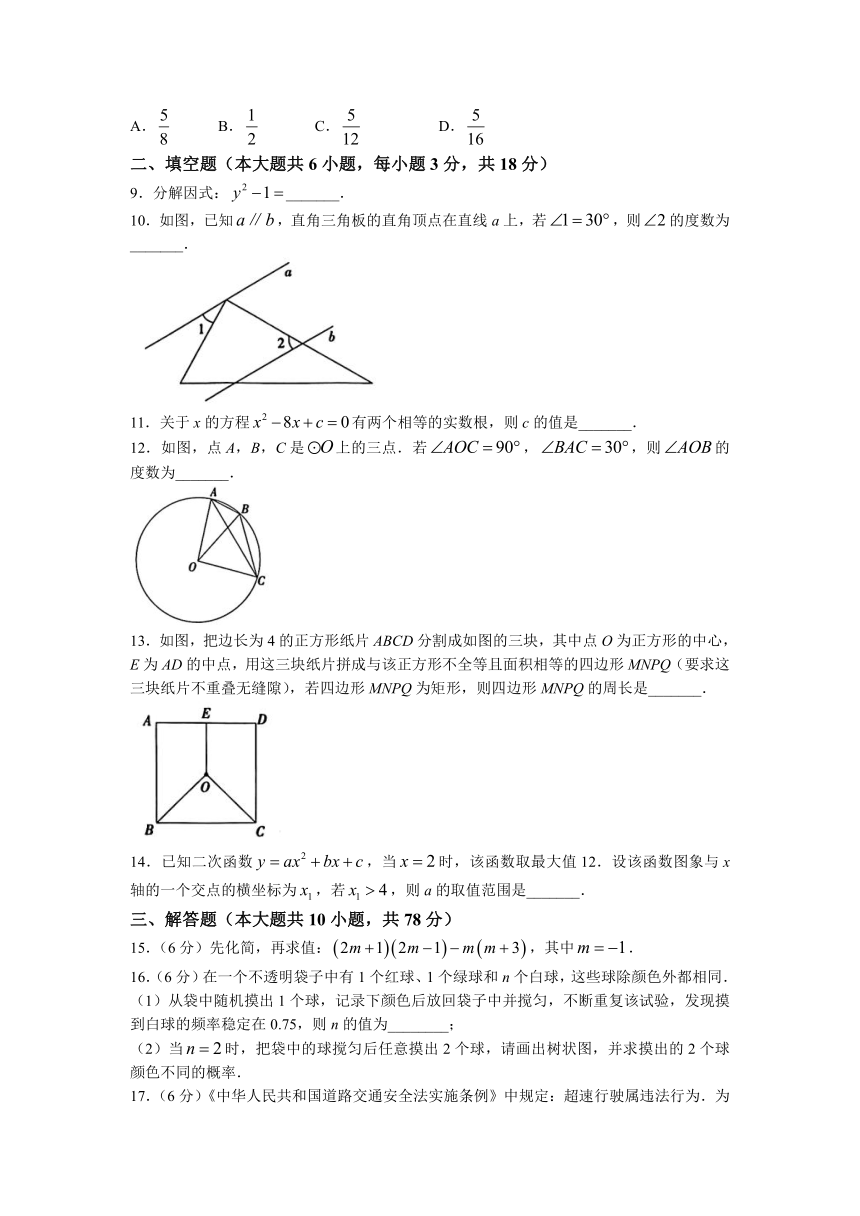
9.分解因式:_______.
10.如图,已知,直角三角板的直角顶点在直线a上,若,则的度数为_______.
11.关于x的方程有两个相等的实数根,则c的值是_______.
12.如图,点A,B,C是上的三点.若,,则的度数为_______.
13.如图,把边长为4的正方形纸片ABCD分割成如图的三块,其中点O为正方形的中心,E为AD的中点,用这三块纸片拼成与该正方形不全等且面积相等的四边形MNPQ(要求这三块纸片不重叠无缝隙),若四边形MNPQ为矩形,则四边形MNPQ的周长是_______.
14.已知二次函数,当时,该函数取最大值12.设该函数图象与x轴的一个交点的横坐标为,若,则a的取值范围是_______.
三、解答题(本大题共10小题,共78分)
15.(6分)先化简,再求值:,其中.
16.(6分)在一个不透明袋子中有1个红球、1个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验,发现摸到白球的频率稳定在0.75,则n的值为________;
(2)当时,把袋中的球搅匀后任意摸出2个球,请画出树状图,并求摸出的2个球颜色不同的概率.
17.(6分)《中华人民共和国道路交通安全法实施条例》中规定:超速行驶属违法行为.为确保行车安全,某一段总路程为270千米的高速公路全程限速120千米时(即行驶过程中任意时刻的车速都不能超过120千米时).以下是王师傅和李师傅全程行驶完这段高速公路后的对话片断.
王师傅:“李师傅,你的平均车速比我的快20%,行驶完全程比我少用了半个小时.”
李师傅:“虽然我的平均车速比你的快,但是我在行驶过程中的最快车速只比我的平均车速快15%,并没有超速啊!”
根据以上对话,你认为李师傅在行驶过程中是否有超速?请说明理由.
18.(7分)在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若,,则菱形ADCF的面积=________.
19.(7分)如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.点A、B均在格点上,仅用无刻度的直尺在给定网格中画图,按步骤完成下列问题:
(1)在图1中,画出格点C,使得.
(2)在图2中,在AB上找点E,使得.
(3)在图3中,在线段MN上找一点F,使得.
20.(7分)在一次社会调查活动中,小亮收集到某公司“健步走运动”团队中20名成员某一天行走的步数,并进行统计,绘制了如下统计表:
组别 步数分组 频数 组内成员的平均步数
A 2 6200
B 10 7150
C 4 7900
D 2 9250
E 2 10050
根据上述信息,解答下列问题:
(1)这20名“健步走运动”团队成员这一天行走的步数的中位数落在________组;
(2)求这20名“健步走运动”团队成员这一天行走的平均步数;
(3)若该团队共有120人,请估计在该团队所有成员中,这一天行走步数不少于7500步的人数.
21.(8分)某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程(千米)、(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
(1)乙组在行驶过程中的速度是________千米/小时.
(2)甲组的汽车排除故障后,立即提速赶往灾区.求甲组提速后与x的函数关系式.
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定.
22.(9分)【方法探索】已知如图①,梯形ABCD中,,,点F、E分别为AC、BD的中点,
求证:
在证明过程中,小明发现连结BF并延长交CD于点K,利用点F为AC中点构造全等三角形,可以实现证明,请按小明的思路完成证明过程.
【方法应用】已知如图②,在等边中,,点A、B分别为ED、EC边上靠近点E的三等分点,连结AC,BD,点P、Q分别为AC,BD的中点,连结PQ,则________.
【解决问题】将图②中的绕点E旋转一周,当A、E、C三点共线时,直接写出PQ的长.
23.(10分)如图,矩形ABCD中,,,点P以每秒2个单位的速度从点A沿AD向终点D运动,将沿PB翻折到处,设运动时间为.
(1)AC长为________.
(2)当点Q落在BC边上时,求t的值.
(3)当点Q落在矩形ABCD的对角线上时,求t的值.
(4)当点Q在矩形ABCD内部、且点P不与A、D重合时,若射线PQ、BQ与矩形两邻边围成的封闭图形存在轴对称图形时(四边形ABQP除外),直接写出t的值.
24.(12分)已知二次函数经过点,对称轴为直线,A、E两点在函数图象上,其横坐标分别为,(n为常数),抛物线在A、E两点之间的部分记为图象G(包括边界).
(1)求二次函数的解析式.
(2)当图象G中,y随x的增大而减小时,求n的取值范围.
(3)若图象G中最大值与最小值的差为1,求n的值.
(4)点B与点A关于原点对称,以AB为对角线作矩形ACBD,且边垂直于坐标轴,当,图象G在矩形内部(包括边界)的最高点为P,右侧的最低点为Q,当P到直线的距离等于Q到y轴的距离时,直接写出n的值.
数学试题
本试卷包括三道大题,共24小题。共6页。全卷满分120分。考试时间为120分钟。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,考生务必将自己的姓名、校区、准考证号填写在答题卡上,并将条形码准确粘贴在条形码区域内。
2.答题时,考生务必按照考试要求在答题卡上的指定区域内作答,在草稿纸、试卷上答题无效。
一、选择题(本大题共8小题,每小题3分,共24分)
1.在,,0,2四个数中,最大的数是( )
A. B.0 C.2 D.
2.据《人民网》报道,在2022卡塔尔世界杯承担开、闭幕式等重要活动的卢塞尔球场是由中国铁建集团承建,其建筑面积为195000平方米.把数字“195000”用科学记数法表示为( )
A. B. C. D.
3.如图是由6个大小相同的小正方体拼成的几何体,当去掉某一个小正方体时,与原几何体比较,则下列说法正确的是( )
A.去掉①,主视图不变 B.去掉②,俯视图不变
C.去掉③,左视图不变 D.去掉④,俯视图不变
4.不等式的解集在数轴上表示,正确的是( )
A. B.
C. D.
5.《九章算术》中记载了一个问题,大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的,那么乙也共有钱50.问:甲,乙两人各带了多少钱?设甲,乙两人持钱的数量分别为x,y,则可列方程组为( )
A. B. C. D.
6.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得,,
,则点A到BC的距离为( )
A. B. C. D.
7.已知,D是AC上一点,尺规在AB上确定一点E,使,则符合要求的作图痕迹是( )
A. B. C. D.
8.如图,在平面直角坐标系中,等腰三角形ABC的底边BC在x轴的正半轴上,顶点A在反比例函数的图象上,延长AB交y轴于点D,若,则的面积是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.分解因式:_______.
10.如图,已知,直角三角板的直角顶点在直线a上,若,则的度数为_______.
11.关于x的方程有两个相等的实数根,则c的值是_______.
12.如图,点A,B,C是上的三点.若,,则的度数为_______.
13.如图,把边长为4的正方形纸片ABCD分割成如图的三块,其中点O为正方形的中心,E为AD的中点,用这三块纸片拼成与该正方形不全等且面积相等的四边形MNPQ(要求这三块纸片不重叠无缝隙),若四边形MNPQ为矩形,则四边形MNPQ的周长是_______.
14.已知二次函数,当时,该函数取最大值12.设该函数图象与x轴的一个交点的横坐标为,若,则a的取值范围是_______.
三、解答题(本大题共10小题,共78分)
15.(6分)先化简,再求值:,其中.
16.(6分)在一个不透明袋子中有1个红球、1个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验,发现摸到白球的频率稳定在0.75,则n的值为________;
(2)当时,把袋中的球搅匀后任意摸出2个球,请画出树状图,并求摸出的2个球颜色不同的概率.
17.(6分)《中华人民共和国道路交通安全法实施条例》中规定:超速行驶属违法行为.为确保行车安全,某一段总路程为270千米的高速公路全程限速120千米时(即行驶过程中任意时刻的车速都不能超过120千米时).以下是王师傅和李师傅全程行驶完这段高速公路后的对话片断.
王师傅:“李师傅,你的平均车速比我的快20%,行驶完全程比我少用了半个小时.”
李师傅:“虽然我的平均车速比你的快,但是我在行驶过程中的最快车速只比我的平均车速快15%,并没有超速啊!”
根据以上对话,你认为李师傅在行驶过程中是否有超速?请说明理由.
18.(7分)在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若,,则菱形ADCF的面积=________.
19.(7分)如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.点A、B均在格点上,仅用无刻度的直尺在给定网格中画图,按步骤完成下列问题:
(1)在图1中,画出格点C,使得.
(2)在图2中,在AB上找点E,使得.
(3)在图3中,在线段MN上找一点F,使得.
20.(7分)在一次社会调查活动中,小亮收集到某公司“健步走运动”团队中20名成员某一天行走的步数,并进行统计,绘制了如下统计表:
组别 步数分组 频数 组内成员的平均步数
A 2 6200
B 10 7150
C 4 7900
D 2 9250
E 2 10050
根据上述信息,解答下列问题:
(1)这20名“健步走运动”团队成员这一天行走的步数的中位数落在________组;
(2)求这20名“健步走运动”团队成员这一天行走的平均步数;
(3)若该团队共有120人,请估计在该团队所有成员中,这一天行走步数不少于7500步的人数.
21.(8分)某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程(千米)、(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
(1)乙组在行驶过程中的速度是________千米/小时.
(2)甲组的汽车排除故障后,立即提速赶往灾区.求甲组提速后与x的函数关系式.
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定.
22.(9分)【方法探索】已知如图①,梯形ABCD中,,,点F、E分别为AC、BD的中点,
求证:
在证明过程中,小明发现连结BF并延长交CD于点K,利用点F为AC中点构造全等三角形,可以实现证明,请按小明的思路完成证明过程.
【方法应用】已知如图②,在等边中,,点A、B分别为ED、EC边上靠近点E的三等分点,连结AC,BD,点P、Q分别为AC,BD的中点,连结PQ,则________.
【解决问题】将图②中的绕点E旋转一周,当A、E、C三点共线时,直接写出PQ的长.
23.(10分)如图,矩形ABCD中,,,点P以每秒2个单位的速度从点A沿AD向终点D运动,将沿PB翻折到处,设运动时间为.
(1)AC长为________.
(2)当点Q落在BC边上时,求t的值.
(3)当点Q落在矩形ABCD的对角线上时,求t的值.
(4)当点Q在矩形ABCD内部、且点P不与A、D重合时,若射线PQ、BQ与矩形两邻边围成的封闭图形存在轴对称图形时(四边形ABQP除外),直接写出t的值.
24.(12分)已知二次函数经过点,对称轴为直线,A、E两点在函数图象上,其横坐标分别为,(n为常数),抛物线在A、E两点之间的部分记为图象G(包括边界).
(1)求二次函数的解析式.
(2)当图象G中,y随x的增大而减小时,求n的取值范围.
(3)若图象G中最大值与最小值的差为1,求n的值.
(4)点B与点A关于原点对称,以AB为对角线作矩形ACBD,且边垂直于坐标轴,当,图象G在矩形内部(包括边界)的最高点为P,右侧的最低点为Q,当P到直线的距离等于Q到y轴的距离时,直接写出n的值.
同课章节目录
