2022-2023学年北师大版数学八年级下册第一章 三角形的证明 同步训练(含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学八年级下册第一章 三角形的证明 同步训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 00:00:00 | ||
图片预览


文档简介
第一章 三角形的证明
一、选择题
1. 一个等腰三角形的顶角是,则它的底角是( )
A. B. C. D.
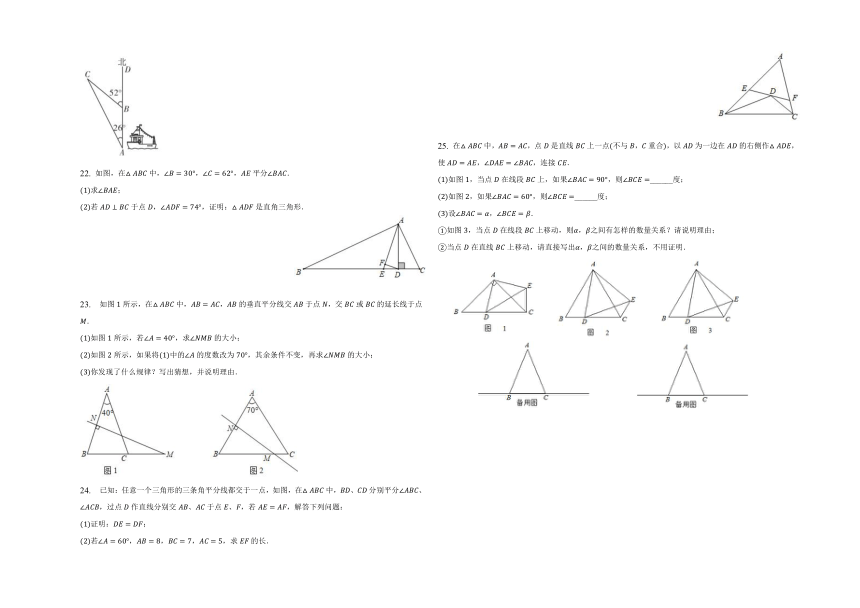
2. 如图,在中,,,是斜边上的高,,那么等于( )
A. B. C. D.
3. 如图,中,边的垂直平分线分别交、于点、,,的周长为,则的周长是( )
A.
B.
C.
D.
4. 如图,在中,,以点为圆心,适当长为半径画弧,分别交、于点,,再分别以点、为圆心,大于为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是( )
A.
B.
C.
D.
5. 将一个有角的三角尺的直角顶点放在一张宽为的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角尺的一边与纸带的一边所在的直线成角,如图,则三角尺的最长边的长为( )
A. B. C. D.
6. 如图,在中,,延长至点,连接,,点为边上一动点,于,于,连接,则的最小值为( )
A. B. C. D.
7. 如图,在中,,线段的垂直平分线交于点,的周长是,则的长为( )
A. B. C. D.
8. 如图,在中,,以顶点为圆心,适当长为半径画弧,分别交边、于点、,现分别以、为圆心,以大于的长为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是( )
A. B. C. D.
9. 如图,在中,,垂直平分斜边交于,是垂足,连接,若,则的长是 ( )
A. B. C. D.
10. 如图,已知,点、分别在、上且,连接,,交于点,连接,过点分别作,,垂足分别为、,下列结论:≌;;平分;如果,则是的中点;其中正确结论的个数为( )
A. 个 B. 个 C. 个 D. 个
二、填空题
11. 等腰三角形一腰上的高与另一腰的夹角为,它的底角为______.
12. 如图,在中,,,,垂足为,若,则的长为______.
13. 如图,在中,的垂直平分线交于点,交于点.
若,,则的长度的取值范围为______;
若,的度数为,则的度数为______用含的式子表示
14. 在中,,作的平分线交于点若,,则的长为______.
15. 如图,在中,,由图中的尺规作图痕迹得到的射线与交于点,点为的中点,连接,若,则的周长为______.
16. 如图,已知,是平分线上一点,,交于点,,垂足为点,且,则等于______.
17. 如图,中,,,,的垂直平分线分别交,于点和,则的周长是____.
18. 如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺成的大正方形,若勾为,弦为,则图中四边形的周长为______.
19. 如图,已知等腰中,,、分别为、上的点,且,则的度数为_______
20. 如图,是边长的等边三角形,动点、同时从、两点出发,分别在、边上匀速移动,它们的速度分别为,,当点到达点时,、两点停止运动,设点的运动时间为,则当_____时,为直角三角形.
三、解答题
21. 如图,上午时,一艘渔船从点处出发,以海里时的速度向正北方向航行,时到达点处从点处测得灯塔在北偏西方向,从点处测得灯塔在北偏西方向,求点处到灯塔的距离.
22. 如图,在中,,,平分.
求;
若于点,,证明:是直角三角形.
23. 如图所示,在中,,的垂直平分线交于点,交或的延长线于点.
如图所示,若,求的大小;
如图所示,如果将中的的度数改为,其余条件不变,再求的大小;
你发现了什么规律?写出猜想,并说明理由.
24. 已知:任意一个三角形的三条角平分线都交于一点,如图,在中,、分别平分、,过点作直线分别交、于点、,若,解答下列问题:
证明:;
若,,,,求的长.
25. 在中,,点是直线上一点不与,重合,以为一边在的右侧作,使,,连接.
如图,当点在线段上,如果,则______度;
如图,如果,则______度;
设,.
如图,当点在线段上移动,则,之间有怎样的数量关系?请说明理由;
当点在直线上移动,请直接写出,之间的数量关系,不用证明.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ; 7、 ; 8、 ; 9、 ; 10、 ;
11、或 ; 12、 ; 13、; ; 14、 ; 15、 ; 16、 ;
17、 ; 18、 ; 19、 ; 20、或
21、解:据题意得,,,
,
,
,
海里,
海里.
处到达塔的距离是海里.
22、解:,,
,
平分,
;
证明:;
,
,
,
,
,
是直角三角形.
23、解:,,
,
是的垂直平分线,
,
.
,,
,
是的垂直平分线,
,
.
,
理由是:,
,
是的垂直平分线,
,
.
24、证明:如图,连接,
、分别平分、,
平分,
又,
;
在上截取,,连接,,
,,
是等边三角形,
,,
,
、分别平分、,
,,
在和中,
,
≌,
,,
,
同理可求,,
是等边三角形,
,
,,,
,,,
.
25、
,
理由:,
.
即.
在与中,,
≌,
.
.
,
,
,
.
或
一、选择题
1. 一个等腰三角形的顶角是,则它的底角是( )
A. B. C. D.
2. 如图,在中,,,是斜边上的高,,那么等于( )
A. B. C. D.
3. 如图,中,边的垂直平分线分别交、于点、,,的周长为,则的周长是( )
A.
B.
C.
D.
4. 如图,在中,,以点为圆心,适当长为半径画弧,分别交、于点,,再分别以点、为圆心,大于为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是( )
A.
B.
C.
D.
5. 将一个有角的三角尺的直角顶点放在一张宽为的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角尺的一边与纸带的一边所在的直线成角,如图,则三角尺的最长边的长为( )
A. B. C. D.
6. 如图,在中,,延长至点,连接,,点为边上一动点,于,于,连接,则的最小值为( )
A. B. C. D.
7. 如图,在中,,线段的垂直平分线交于点,的周长是,则的长为( )
A. B. C. D.
8. 如图,在中,,以顶点为圆心,适当长为半径画弧,分别交边、于点、,现分别以、为圆心,以大于的长为半径画弧,两弧交于点,作射线交边于点,若,,则的面积是( )
A. B. C. D.
9. 如图,在中,,垂直平分斜边交于,是垂足,连接,若,则的长是 ( )
A. B. C. D.
10. 如图,已知,点、分别在、上且,连接,,交于点,连接,过点分别作,,垂足分别为、,下列结论:≌;;平分;如果,则是的中点;其中正确结论的个数为( )
A. 个 B. 个 C. 个 D. 个
二、填空题
11. 等腰三角形一腰上的高与另一腰的夹角为,它的底角为______.
12. 如图,在中,,,,垂足为,若,则的长为______.
13. 如图,在中,的垂直平分线交于点,交于点.
若,,则的长度的取值范围为______;
若,的度数为,则的度数为______用含的式子表示
14. 在中,,作的平分线交于点若,,则的长为______.
15. 如图,在中,,由图中的尺规作图痕迹得到的射线与交于点,点为的中点,连接,若,则的周长为______.
16. 如图,已知,是平分线上一点,,交于点,,垂足为点,且,则等于______.
17. 如图,中,,,,的垂直平分线分别交,于点和,则的周长是____.
18. 如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺成的大正方形,若勾为,弦为,则图中四边形的周长为______.
19. 如图,已知等腰中,,、分别为、上的点,且,则的度数为_______
20. 如图,是边长的等边三角形,动点、同时从、两点出发,分别在、边上匀速移动,它们的速度分别为,,当点到达点时,、两点停止运动,设点的运动时间为,则当_____时,为直角三角形.
三、解答题
21. 如图,上午时,一艘渔船从点处出发,以海里时的速度向正北方向航行,时到达点处从点处测得灯塔在北偏西方向,从点处测得灯塔在北偏西方向,求点处到灯塔的距离.
22. 如图,在中,,,平分.
求;
若于点,,证明:是直角三角形.
23. 如图所示,在中,,的垂直平分线交于点,交或的延长线于点.
如图所示,若,求的大小;
如图所示,如果将中的的度数改为,其余条件不变,再求的大小;
你发现了什么规律?写出猜想,并说明理由.
24. 已知:任意一个三角形的三条角平分线都交于一点,如图,在中,、分别平分、,过点作直线分别交、于点、,若,解答下列问题:
证明:;
若,,,,求的长.
25. 在中,,点是直线上一点不与,重合,以为一边在的右侧作,使,,连接.
如图,当点在线段上,如果,则______度;
如图,如果,则______度;
设,.
如图,当点在线段上移动,则,之间有怎样的数量关系?请说明理由;
当点在直线上移动,请直接写出,之间的数量关系,不用证明.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ; 7、 ; 8、 ; 9、 ; 10、 ;
11、或 ; 12、 ; 13、; ; 14、 ; 15、 ; 16、 ;
17、 ; 18、 ; 19、 ; 20、或
21、解:据题意得,,,
,
,
,
海里,
海里.
处到达塔的距离是海里.
22、解:,,
,
平分,
;
证明:;
,
,
,
,
,
是直角三角形.
23、解:,,
,
是的垂直平分线,
,
.
,,
,
是的垂直平分线,
,
.
,
理由是:,
,
是的垂直平分线,
,
.
24、证明:如图,连接,
、分别平分、,
平分,
又,
;
在上截取,,连接,,
,,
是等边三角形,
,,
,
、分别平分、,
,,
在和中,
,
≌,
,,
,
同理可求,,
是等边三角形,
,
,,,
,,,
.
25、
,
理由:,
.
即.
在与中,,
≌,
.
.
,
,
,
.
或
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
