第三章 勾股定理复习学案
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理复习学案
【本章目标】
经历勾股定理及直角三角形判别条件的探索过程,并能利用它们解决简单问题。
【知识梳理】
1.勾股定理: ,几何语言表述为:
.在Rt△ABC中,,则
勾股数:能够构成直角三角形的三边长的三个 称为勾股数,即中,,,为正整数时,称,,为一组勾股数
2.如果三角形的三边长a、b、c有关系: ,
那么这个三角形是直角三角形.
3.勾股定理的应用:最短路程、构造直角三角形
【典型例题】
考点一 勾股定理
例1.在直角三角形中,一条直角边长为5,另一条直角边边长为12,则第三条边的平方为( )
A.169 B. 119 C. 169或119 D. 以上都不对
例2.如图一,∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长为
巩固训练1
等腰三角形的底边长为6,底边上的中线长为4,它的腰长为 .
考点二 直角三角形的判别条件
例3.如图二,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13 求四边形ABCD的面积。
例4.三角形的三边长为,则这个三角形是( ) 三角形
A等边 B钝角 C 直角 D锐角
巩固训练2
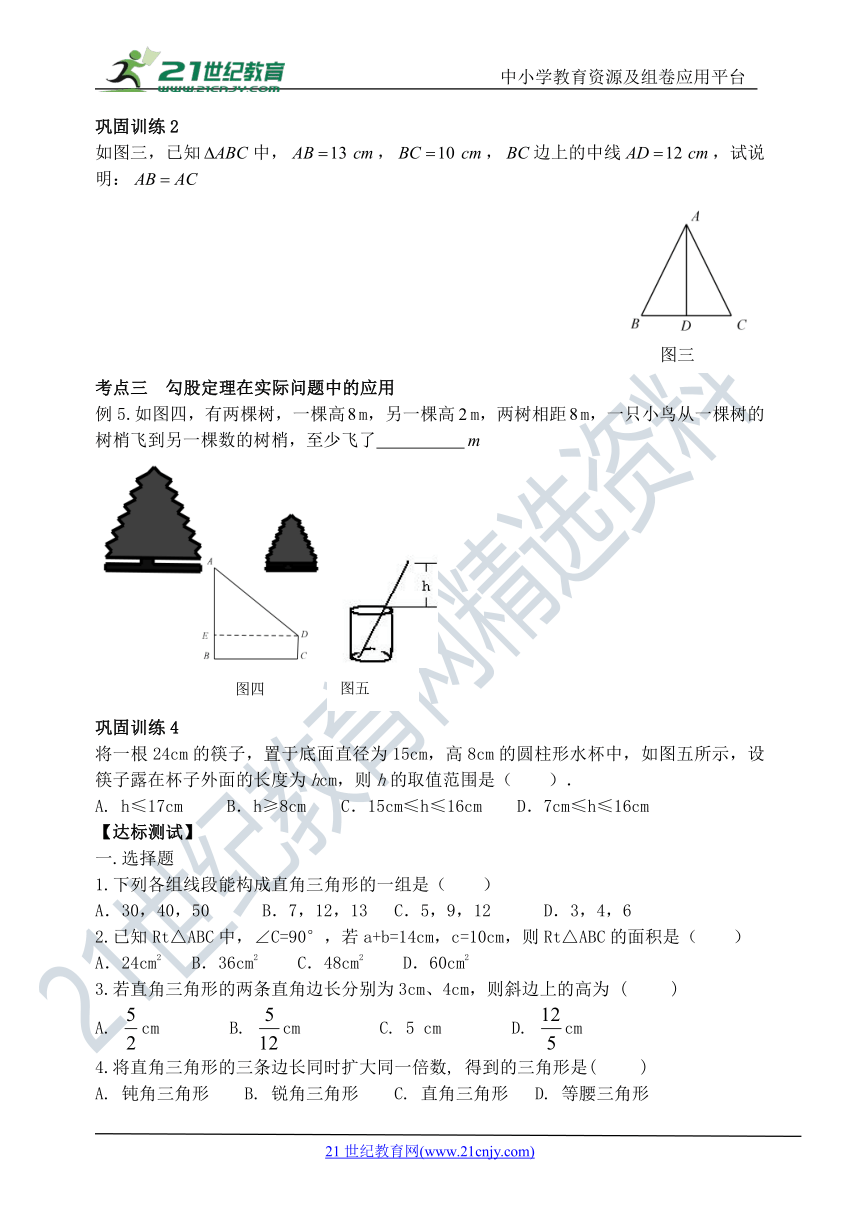
如图三,已知中,,,边上的中线,试说明:
考点三 勾股定理在实际问题中的应用
例5.如图四,有两棵树,一棵高m,另一棵高m,两树相距m,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了
巩固训练4
将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图五所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是( ).
h≤17cm B.h≥8cm C.15cm≤h≤16cm D.7cm≤h≤16cm
【达标测试】
一.选择题
1.下列各组线段能构成直角三角形的一组是( )
A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6
2.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
3.若直角三角形的两条直角边长分别为3cm、4cm,则斜边上的高为 ( )
A. cm B. cm C. 5 cm D. cm
4.将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等腰三角形
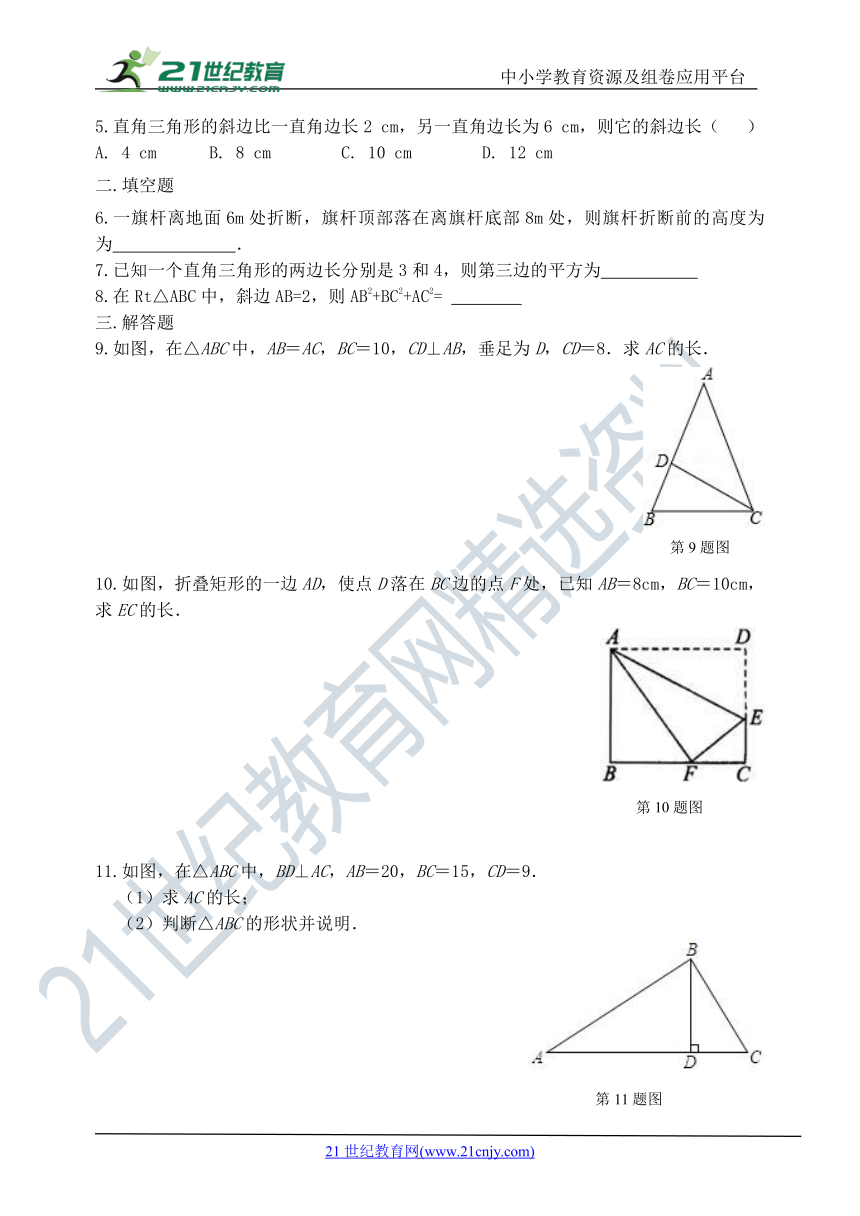
5.直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( )
A. 4 cm B. 8 cm C. 10 cm D. 12 cm
二.填空题
6.一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,则旗杆折断前的高度为为 .
7.已知一个直角三角形的两边长分别是3和4,则第三边的平方为
8.在Rt△ABC中,斜边AB=2,则AB2+BC2+AC2=
三.解答题
9.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=8.求AC的长.
10.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
11.如图,在△ABC中,BD⊥AC,AB=20,BC=15,CD=9.
(1)求AC的长;
(2)判断△ABC的形状并说明.
12.如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求△BCD的面积.
13.已知:如图,在△ABC中,AC=9,AB=12,BC=15,AD是BC边上的高.
(1)试说明:△ABC是直角三角形;
(2)求AD的长.
七年级数学(上)第三章勾股定理复习学案参考答案
【典型例题】
C 例2. 4 巩固训练1. 5 例3. 36 例4. C 例5. 10
巩固训练4. D
【达标测试】
1-5 AADCC 6. 16m 7.25或7 8.8
9.解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△BCD中,BD2=BC2—CD2,BD=6,
设AC=AB=x,则AD=x﹣6,
在Rt△ACD中,AC2=AD2+CD2,即x2=(x﹣6)2+82,
解得,x=,即AC=.
10.解:∵四边形ABCD为矩形,
∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,
∵折叠矩形的一边AD,使点D落在BC边的点F处
∴AF=AD=10,DE=EF,
在Rt△ABF中,BF2=AF2-AB2=36,BF=6
∴FC=BC﹣BF=4,
设EC=x,则DE=8﹣x,EF=8﹣x,
在Rt△EFC中,
∵EC2+FC2=EF2,
∴x2+42=(8﹣x)2,解得x=3,
∴EC的长为3cm.
11.解:(1)∵在△ABC中,CD⊥AB于D,AB=20,BC=15,DC=9,
∴BD=,
AD=,
∴AC=AD+BC=16+9=25;
(2)∵AC=25,BC=15,AB=20,202+152=252,
∴△ABC是直角三角形.
12,解:(1)∵∠A=90°,AB=9,AC=12
∴BC==15,
(2)∵BC=15,BD=8,CD=17
∴BC2+BD2=CD2
∴△BCD是直角三角形
∴S△BCD=×15×8=60.
13.解:(1)∵AC=9 AB=12 BC=15,
∴AC2=81,AB2=144,BC2=225,
∴AC2+AB2=BC2,
∴∠BAC=90°,
∴△ABC是直角三角形;
(2)∵S△ABC=AB AC=BC AD,
∴AD==.
B
a
c
C
A
b
图一
图二
图三
图四
图五
第9题图
第10题图
第11题图
第12题图
第13题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第三章 勾股定理复习学案
【本章目标】
经历勾股定理及直角三角形判别条件的探索过程,并能利用它们解决简单问题。
【知识梳理】
1.勾股定理: ,几何语言表述为:
.在Rt△ABC中,,则
勾股数:能够构成直角三角形的三边长的三个 称为勾股数,即中,,,为正整数时,称,,为一组勾股数
2.如果三角形的三边长a、b、c有关系: ,
那么这个三角形是直角三角形.
3.勾股定理的应用:最短路程、构造直角三角形
【典型例题】
考点一 勾股定理
例1.在直角三角形中,一条直角边长为5,另一条直角边边长为12,则第三条边的平方为( )
A.169 B. 119 C. 169或119 D. 以上都不对
例2.如图一,∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长为
巩固训练1
等腰三角形的底边长为6,底边上的中线长为4,它的腰长为 .
考点二 直角三角形的判别条件
例3.如图二,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13 求四边形ABCD的面积。
例4.三角形的三边长为,则这个三角形是( ) 三角形
A等边 B钝角 C 直角 D锐角
巩固训练2
如图三,已知中,,,边上的中线,试说明:
考点三 勾股定理在实际问题中的应用
例5.如图四,有两棵树,一棵高m,另一棵高m,两树相距m,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了
巩固训练4
将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图五所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是( ).
h≤17cm B.h≥8cm C.15cm≤h≤16cm D.7cm≤h≤16cm
【达标测试】
一.选择题
1.下列各组线段能构成直角三角形的一组是( )
A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6
2.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
3.若直角三角形的两条直角边长分别为3cm、4cm,则斜边上的高为 ( )
A. cm B. cm C. 5 cm D. cm
4.将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等腰三角形
5.直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( )
A. 4 cm B. 8 cm C. 10 cm D. 12 cm
二.填空题
6.一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,则旗杆折断前的高度为为 .
7.已知一个直角三角形的两边长分别是3和4,则第三边的平方为
8.在Rt△ABC中,斜边AB=2,则AB2+BC2+AC2=
三.解答题
9.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=8.求AC的长.
10.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
11.如图,在△ABC中,BD⊥AC,AB=20,BC=15,CD=9.
(1)求AC的长;
(2)判断△ABC的形状并说明.
12.如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求△BCD的面积.
13.已知:如图,在△ABC中,AC=9,AB=12,BC=15,AD是BC边上的高.
(1)试说明:△ABC是直角三角形;
(2)求AD的长.
七年级数学(上)第三章勾股定理复习学案参考答案
【典型例题】
C 例2. 4 巩固训练1. 5 例3. 36 例4. C 例5. 10
巩固训练4. D
【达标测试】
1-5 AADCC 6. 16m 7.25或7 8.8
9.解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△BCD中,BD2=BC2—CD2,BD=6,
设AC=AB=x,则AD=x﹣6,
在Rt△ACD中,AC2=AD2+CD2,即x2=(x﹣6)2+82,
解得,x=,即AC=.
10.解:∵四边形ABCD为矩形,
∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,
∵折叠矩形的一边AD,使点D落在BC边的点F处
∴AF=AD=10,DE=EF,
在Rt△ABF中,BF2=AF2-AB2=36,BF=6
∴FC=BC﹣BF=4,
设EC=x,则DE=8﹣x,EF=8﹣x,
在Rt△EFC中,
∵EC2+FC2=EF2,
∴x2+42=(8﹣x)2,解得x=3,
∴EC的长为3cm.
11.解:(1)∵在△ABC中,CD⊥AB于D,AB=20,BC=15,DC=9,
∴BD=,
AD=,
∴AC=AD+BC=16+9=25;
(2)∵AC=25,BC=15,AB=20,202+152=252,
∴△ABC是直角三角形.
12,解:(1)∵∠A=90°,AB=9,AC=12
∴BC==15,
(2)∵BC=15,BD=8,CD=17
∴BC2+BD2=CD2
∴△BCD是直角三角形
∴S△BCD=×15×8=60.
13.解:(1)∵AC=9 AB=12 BC=15,
∴AC2=81,AB2=144,BC2=225,
∴AC2+AB2=BC2,
∴∠BAC=90°,
∴△ABC是直角三角形;
(2)∵S△ABC=AB AC=BC AD,
∴AD==.
B
a
c
C
A
b
图一
图二
图三
图四
图五
第9题图
第10题图
第11题图
第12题图
第13题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
