2.3 简单的轴对称图形(1) 课件(共24张PPT)
文档属性
| 名称 | 2.3 简单的轴对称图形(1) 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
线段是轴对称图形吗?
问题:你对线段有哪些认识
学习目标
1.探索并掌握线段的垂直平分线的性质;
2.掌握线段的垂直平分线的尺规作图。
3.在“操作--探究---归纳---说理”的过程中学会有条理地思考和表达,提高演绎推理能力。
线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?这条对称轴与线段存在着什么关系?
A
B
按照下面的步骤做一做:
1)在纸片上画一条线段AB,
A
B
对折AB使点A,B重合,
折痕与AB的交点为O;
O
2)在折痕上任取一点C,
C
沿CA将纸折叠;
3)把纸展,
A
O
得到折痕CA和CB。
B
C
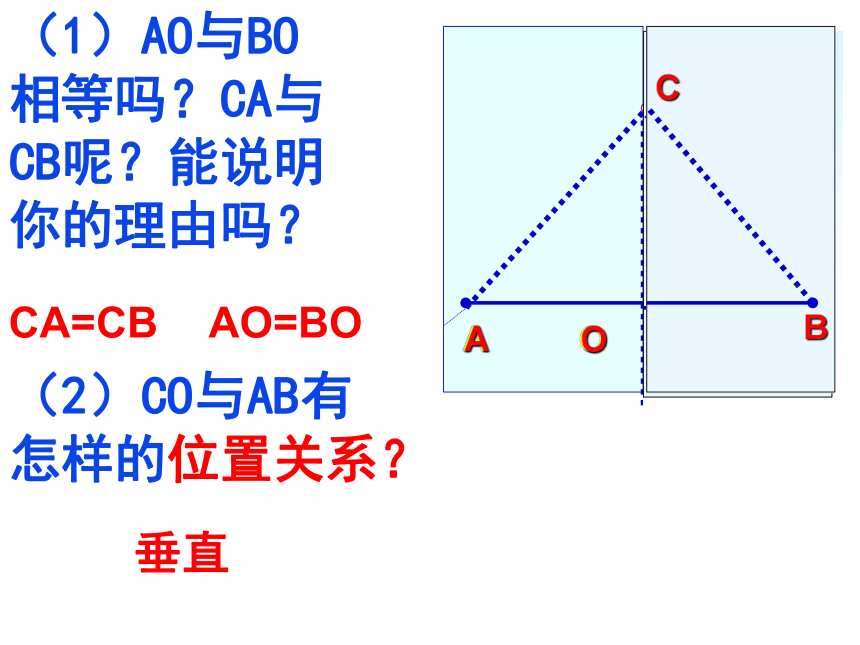
(2)CO与AB有怎样的位置关系?
(1)AO与BO相等吗?CA与CB呢?能说明你的理由吗?
垂直
AO=BO
CA=CB
C
A
O
B
C
A
O
B
C
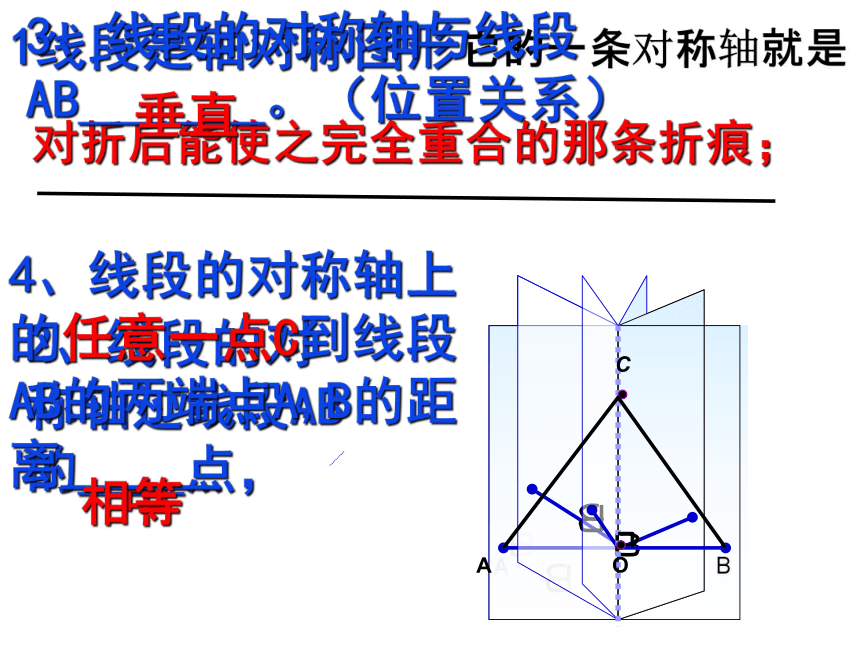
1线段是轴对称图形
A
B
A
B
它的一条对称轴就是
对折后能使之完全重合的那条折痕;
2、线段的对称轴过线段AB的 点,
中
O
C
3、线段的对称轴与线段AB 。(位置关系)
垂直
4、线段的对称轴上的任意一点C到线段AB的两端点A,B的距离______
相等
A
B
O
1 垂直且平分一条线段的直线叫做这条线段的垂直平分线。
线段的垂直平分线
2 线段的对称轴是这条线段的 垂直平分线
A
B
O
线段的垂直平分线
性质:线段垂直平分线上的任意点到这条线段两个端点的距离相等。
用几何语言表达
∵
AO=BO,MO⊥AB
M
(已知)
∴
MA=MB
(线段的垂直平分线上的点到这条线段两个端点的距离相等)
2.如图,△ABC中,AD垂直平分边BC,AB=5,那么AC= .
A
B
D
C
5
1.线段的对称轴是它的 。
垂直平分线
练习题
1.在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E,D,BE=6,求△BCE的周长.
解:因为DE是线段BC的
垂直平分线
所以EC=EB=6
所以△BCE的周长=
如图,已知线段AB,画出它的垂直平分线.
尺规作图做垂直平分线
观察领悟作法,探索思考证明方法:
A
B
C
D
尺规作线段的中垂线
作法:(1)以点A为圆心,以大于AB一半的长为半径画弧;
(2)以点B为圆心,以同样的长为半径画弧,两弧的交点记为C、D;
(3)经过点C、D作直线CD.
直线CD即为所求.
在直线AB上找一点P,使点P到M、N两点的距离相等。
M
A
B
N
P
解:
作线段MN的垂直平分线,
交直线AB于点P,
点P即为所求点。
如图:
在△ABC中用刻度尺和量角器画出线段AB、BC、CA的垂直平分线,看看三条垂直平分线的位置有什么关系
A
B
C
∟
∟
∟
P
解答:
三条垂直平分线交于一点
思考:若设交点为P,连接PA、PB、PC,那么PA、PB、PC有什么关系?
结论:三角形三条边垂直平分线的交点到三个顶点的距离相等。
锐角三角形三边的垂直平分线的交点在它的内部
钝角三角形三边的垂直平分线的交点在它的外部
直角三角形三边的垂直平分线的交点在它的一条边上
总结
A
B
C
A、B、C三点表示三个镇,随着乡镇外资、集体、个体工业的发展需要,现三镇联合建造一个变电所,要求变电所到三镇的距离相等,请你作出变电所的位置(用点P表示)
1、分别连接AB、BC
2、分别作线段AB、BC的垂直平分线
两直线交于点P
则点P为所求的变电所的位置
P
如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
4
6
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
26
如图,已知点D在AB的垂直平分线上,如果AC=5cm,BC=4cm,那么△BDC的周长是( )cm。
∟
A
D
E
B
C
M
N
A. 6
B. 7
C. 8
D. 9
D
1、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
街道
C
D
A
B
街道
C
2、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
D
A
B
P
小结
1. 垂直于一条线段并且平分它的直线叫这条线段的垂直平分线。
2. 线段是轴对称图形,它的垂直平分线是它的一条对称轴 .
3. 线段垂直平分线上的点到这条线段两个端点的距离相等 .
当堂达标
见导学案
线段是轴对称图形吗?
问题:你对线段有哪些认识
学习目标
1.探索并掌握线段的垂直平分线的性质;
2.掌握线段的垂直平分线的尺规作图。
3.在“操作--探究---归纳---说理”的过程中学会有条理地思考和表达,提高演绎推理能力。
线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?这条对称轴与线段存在着什么关系?
A
B
按照下面的步骤做一做:
1)在纸片上画一条线段AB,
A
B
对折AB使点A,B重合,
折痕与AB的交点为O;
O
2)在折痕上任取一点C,
C
沿CA将纸折叠;
3)把纸展,
A
O
得到折痕CA和CB。
B
C
(2)CO与AB有怎样的位置关系?
(1)AO与BO相等吗?CA与CB呢?能说明你的理由吗?
垂直
AO=BO
CA=CB
C
A
O
B
C
A
O
B
C
1线段是轴对称图形
A
B
A
B
它的一条对称轴就是
对折后能使之完全重合的那条折痕;
2、线段的对称轴过线段AB的 点,
中
O
C
3、线段的对称轴与线段AB 。(位置关系)
垂直
4、线段的对称轴上的任意一点C到线段AB的两端点A,B的距离______
相等
A
B
O
1 垂直且平分一条线段的直线叫做这条线段的垂直平分线。
线段的垂直平分线
2 线段的对称轴是这条线段的 垂直平分线
A
B
O
线段的垂直平分线
性质:线段垂直平分线上的任意点到这条线段两个端点的距离相等。
用几何语言表达
∵
AO=BO,MO⊥AB
M
(已知)
∴
MA=MB
(线段的垂直平分线上的点到这条线段两个端点的距离相等)
2.如图,△ABC中,AD垂直平分边BC,AB=5,那么AC= .
A
B
D
C
5
1.线段的对称轴是它的 。
垂直平分线
练习题
1.在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E,D,BE=6,求△BCE的周长.
解:因为DE是线段BC的
垂直平分线
所以EC=EB=6
所以△BCE的周长=
如图,已知线段AB,画出它的垂直平分线.
尺规作图做垂直平分线
观察领悟作法,探索思考证明方法:
A
B
C
D
尺规作线段的中垂线
作法:(1)以点A为圆心,以大于AB一半的长为半径画弧;
(2)以点B为圆心,以同样的长为半径画弧,两弧的交点记为C、D;
(3)经过点C、D作直线CD.
直线CD即为所求.
在直线AB上找一点P,使点P到M、N两点的距离相等。
M
A
B
N
P
解:
作线段MN的垂直平分线,
交直线AB于点P,
点P即为所求点。
如图:
在△ABC中用刻度尺和量角器画出线段AB、BC、CA的垂直平分线,看看三条垂直平分线的位置有什么关系
A
B
C
∟
∟
∟
P
解答:
三条垂直平分线交于一点
思考:若设交点为P,连接PA、PB、PC,那么PA、PB、PC有什么关系?
结论:三角形三条边垂直平分线的交点到三个顶点的距离相等。
锐角三角形三边的垂直平分线的交点在它的内部
钝角三角形三边的垂直平分线的交点在它的外部
直角三角形三边的垂直平分线的交点在它的一条边上
总结
A
B
C
A、B、C三点表示三个镇,随着乡镇外资、集体、个体工业的发展需要,现三镇联合建造一个变电所,要求变电所到三镇的距离相等,请你作出变电所的位置(用点P表示)
1、分别连接AB、BC
2、分别作线段AB、BC的垂直平分线
两直线交于点P
则点P为所求的变电所的位置
P
如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
4
6
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
26
如图,已知点D在AB的垂直平分线上,如果AC=5cm,BC=4cm,那么△BDC的周长是( )cm。
∟
A
D
E
B
C
M
N
A. 6
B. 7
C. 8
D. 9
D
1、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
街道
C
D
A
B
街道
C
2、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
D
A
B
P
小结
1. 垂直于一条线段并且平分它的直线叫这条线段的垂直平分线。
2. 线段是轴对称图形,它的垂直平分线是它的一条对称轴 .
3. 线段垂直平分线上的点到这条线段两个端点的距离相等 .
当堂达标
见导学案
