勾股定理(2)的证明及应用[上学期]
图片预览




文档简介
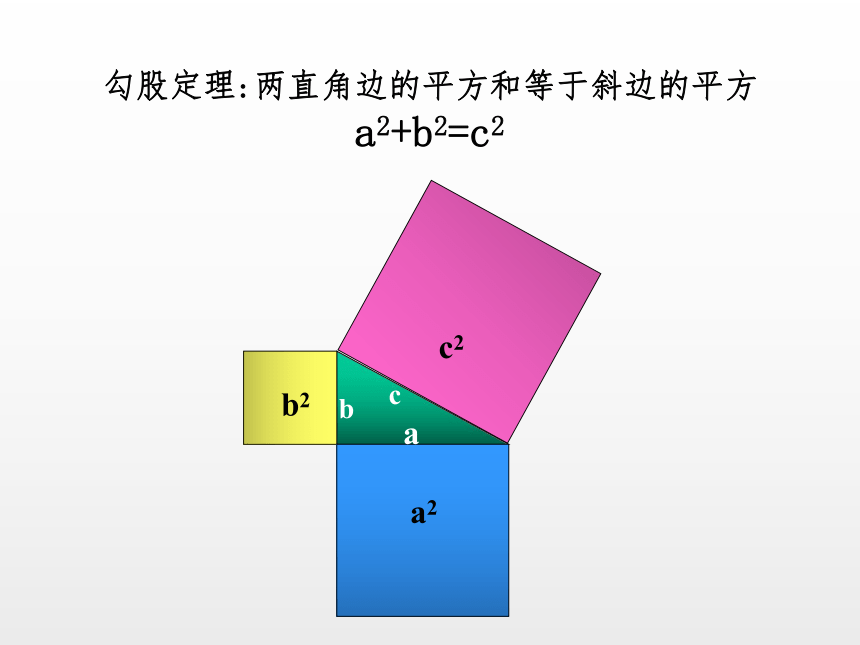
课件15张PPT。勾股定理(2)勾股定理的证明及应用勾股定理:两直角边的平方和等于斜边的平方
a2+b2=c2
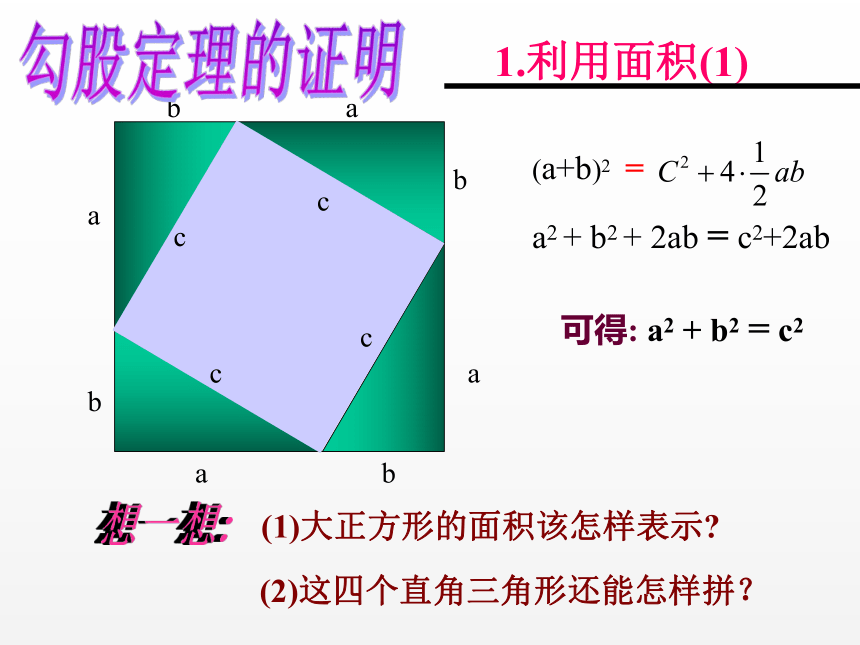
abc右图有四个全等的直角三角形,用这四个三角形拼一拼、摆一摆,看看是否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?并与同伴交流。拼一拼(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2(2)这四个直角三角形还能怎样拼?勾股定理的证明(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2ab勾股定理的证明 读一读
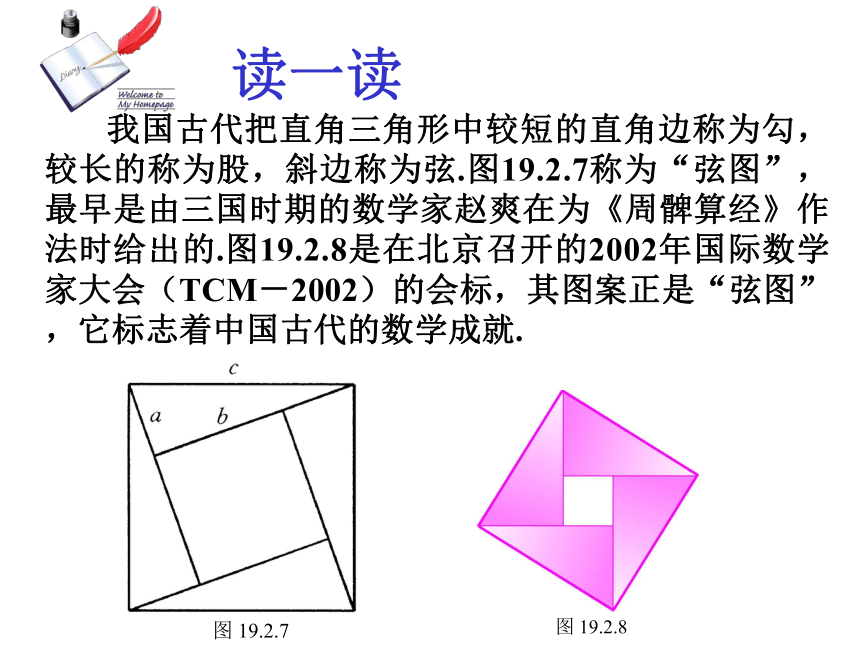
我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.图19.2.7称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图19.2.8是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
已知:在直角△ABC中,∠ACB=90°CD⊥AB,垂足为D。 想一想:图中有哪些三角形是相似的?下列线段有 怎样的关系? 解: △ACD∽△ABC∽△CBD可得: (1) CD2=AD·BD
(2) AC2=AD·AB
(3) BC2=BD·AB则有: AC2+BC2=(AD+BD) ·AB即: AC2+BC2=AB2勾股定理的证明2.利用相似三角形基础练习1、下列各组数据能判断三角形是直角三角形的是
A、三边长都是2; B、三边长分别是3、4、3;
C、三边长分别是12、5、13;D、三边长分别是7、4、54、菱形的两条对角线长分别是6和8,它的高为____2、三角形的三边长分别为4、5、3,
则三角形的面积为_________5、等边三角形的边长为6,则它的面积为_______3、若直角三角形的两边长分别为5, 12,
则第三边长为_________问题(1): 如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
解 在直角三角形ABC中,
AC=160米,BC=128米,
根据勾股定理可得
= 96(米)
答:从点A穿过湖到点B有96米.问题(2):如图,两艘军同时从某军港口出发执行任务,甲舰以30海里/时的速度向西北方向航行,乙舰以40海里/时的速度向西南方向航行,1.5小时后两舰相距多远?问题(3): 有一架3米长的梯子搭在墙上,刚好与墙 头对齐,此时梯脚与墙的距离是1米, (1)求墙的高度? (精确到0.1)解:∴AC=∵AB=3,BC=1==≈2.8(米)2.3米(2)若梯子的顶端下滑50厘米,
底端将水平动多少米?练 习 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?ABC 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米? 练 习CD解:过点B作BC⊥AD于C,得Rt⊿ABC
由题意,有AC=8-3+1=6千米,
BC=2+6=8千米
∴AB=
=10(千米)
答:点A到点B的直线距离是10千米你学会了吗?(1)掌握勾股定理及利用拼图来证明的方法。
(2)勾股定理来自于实践,注意在实践中的应用。
(3)多动手、动脑,
很多知识是在做的过程中发现的。美丽的勾股树
你可能去过森林公园,看到过许许多多千姿百态的植物.可是你是否见过如下的勾股树呢?
你知道这是如何画出来的吗?仔细看看,你就会发现那一个个细小的部分正是我们学过的勾股图,一个一个连接在一起,构成了多么奇妙美丽的勾股树!动手画画看,相信你也能画出其他形态的勾股树.
美丽的勾股树拓展
abc右图有四个全等的直角三角形,用这四个三角形拼一拼、摆一摆,看看是否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?并与同伴交流。拼一拼(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2(2)这四个直角三角形还能怎样拼?勾股定理的证明(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2ab勾股定理的证明 读一读
我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.图19.2.7称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图19.2.8是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
已知:在直角△ABC中,∠ACB=90°CD⊥AB,垂足为D。 想一想:图中有哪些三角形是相似的?下列线段有 怎样的关系? 解: △ACD∽△ABC∽△CBD可得: (1) CD2=AD·BD
(2) AC2=AD·AB
(3) BC2=BD·AB则有: AC2+BC2=(AD+BD) ·AB即: AC2+BC2=AB2勾股定理的证明2.利用相似三角形基础练习1、下列各组数据能判断三角形是直角三角形的是
A、三边长都是2; B、三边长分别是3、4、3;
C、三边长分别是12、5、13;D、三边长分别是7、4、54、菱形的两条对角线长分别是6和8,它的高为____2、三角形的三边长分别为4、5、3,
则三角形的面积为_________5、等边三角形的边长为6,则它的面积为_______3、若直角三角形的两边长分别为5, 12,
则第三边长为_________问题(1): 如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
解 在直角三角形ABC中,
AC=160米,BC=128米,
根据勾股定理可得
= 96(米)
答:从点A穿过湖到点B有96米.问题(2):如图,两艘军同时从某军港口出发执行任务,甲舰以30海里/时的速度向西北方向航行,乙舰以40海里/时的速度向西南方向航行,1.5小时后两舰相距多远?问题(3): 有一架3米长的梯子搭在墙上,刚好与墙 头对齐,此时梯脚与墙的距离是1米, (1)求墙的高度? (精确到0.1)解:∴AC=∵AB=3,BC=1==≈2.8(米)2.3米(2)若梯子的顶端下滑50厘米,
底端将水平动多少米?练 习 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?ABC 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏点B的直线距离是多少千米? 练 习CD解:过点B作BC⊥AD于C,得Rt⊿ABC
由题意,有AC=8-3+1=6千米,
BC=2+6=8千米
∴AB=
=10(千米)
答:点A到点B的直线距离是10千米你学会了吗?(1)掌握勾股定理及利用拼图来证明的方法。
(2)勾股定理来自于实践,注意在实践中的应用。
(3)多动手、动脑,
很多知识是在做的过程中发现的。美丽的勾股树
你可能去过森林公园,看到过许许多多千姿百态的植物.可是你是否见过如下的勾股树呢?
你知道这是如何画出来的吗?仔细看看,你就会发现那一个个细小的部分正是我们学过的勾股图,一个一个连接在一起,构成了多么奇妙美丽的勾股树!动手画画看,相信你也能画出其他形态的勾股树.
美丽的勾股树拓展
