简单线性规划[上学期]
图片预览



文档简介
课件13张PPT。简单线性规划徐青问题1:以二元一次方程x+y-1=0的解为坐标点的集合
表示什么图形?问题2:以二元一次不等式x+y-1>0的解为坐标点的集合
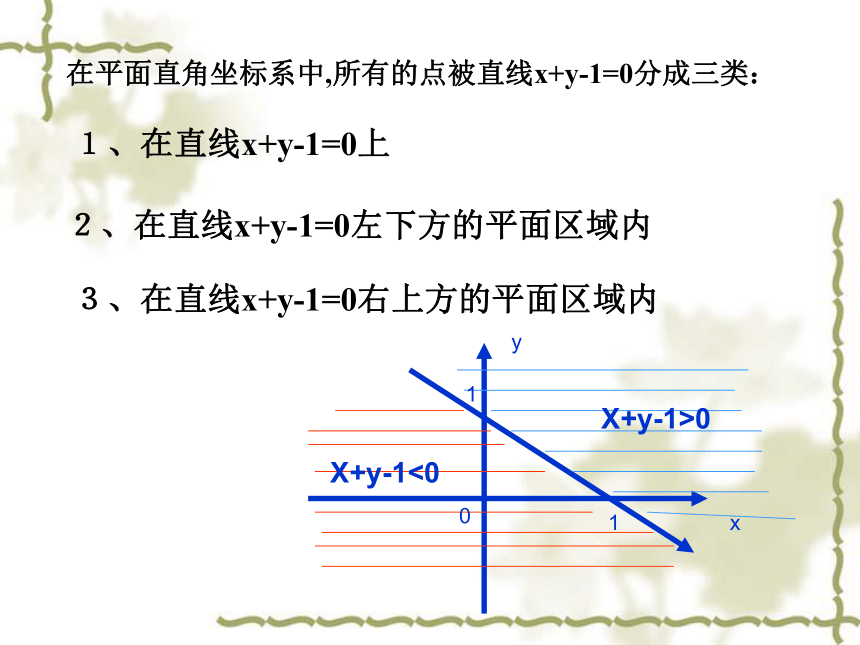
表示什么图形?1、用二元一次不等式(组)表示平面区域在平面直角坐标系中,所有的点被直线x+y-1=0分成三类:1、在直线x+y-1=0上2、在直线x+y-1=0左下方的平面区域内3、在直线x+y-1=0右上方的平面区域内0xyX+y-1>0X+y-1<011小结一:一般的,二元一次不等式Ax+By+C>0在平面坐标系中表示直线Ax+By+C=0某一侧所有点组成的区域。⒈⒉把直线画成虚线以表示区域不包括边界直线;把直线画成实线以表示区域包括边界直线;小技巧:在直线的某一侧取一个特殊点(x0,y0),代入Ax+By+C(A>0)中,
若结果为正,则这个点所在的区域表示Ax+By+C>0
若结果为负,则这个点所在的区域表示Ax+By+C<0
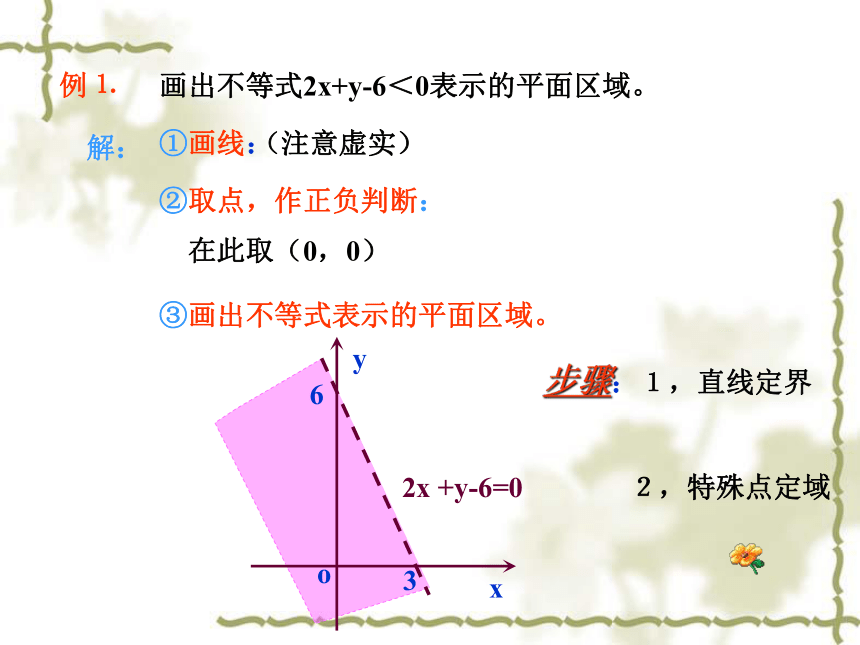
特殊的,当C≠0时,可以取(0,0)作为特殊点。例⒈画出不等式2x+y-6<0表示的平面区域。解:①画线:(注意虚实)②取点,作正负判断:在此取(0,0)③画出不等式表示的平面区域。36步骤:1,直线定界
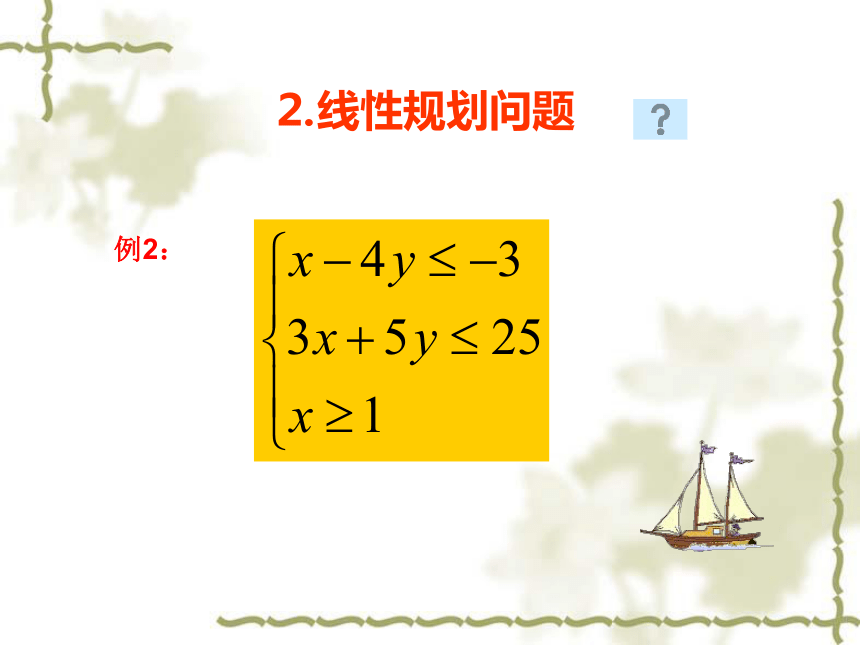
2,特殊点定域⒉线性规划问题例2:基本概念:⒈z=2x+y⒊象此问题一样,求线性目标函数在线性约束条件下的最值
的问题统称为线性规划问题。小结二:对于线性目标函数z=Ax+By1、当B>0时,当直线过可行域且
在y轴上截距最大时,z的值最大,
在y轴上截距最小时,z的值最小。2、当B<0时,当直线过可行域且
在y轴上截距最大时,z的值最小,
在y轴上截距最小时,z的值最大。解线性规划问题的步骤: (2)移:设z=0,画出直线,利用平移的方法找
出与可行域有公共点且纵截距最大
或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;例3:在上题的约束条件下,的最大值和最小值是什么?解:当x=1,y=1时,有最小值为2;当x=5,y=2时,有最大值为29.例4:若P(x,y)的坐标满足上约束条件,点O为坐
标原点,则的最小值是例5:若P(x,y)的坐标满足上约束条件,的最大值是4.43、可行域上的最优解
应用例6:某人有一楼房,室内面积共180 ,
分隔两类房间作为客房。
大房间每间面积为18 ,可住5人,每人每天40元; 小房间每间面积为15 ,可住3人,住宿费每人每天50元。
装修大房间每间要1000元,装修小房间每间要600元。如果他只能筹款8000元用于装修,且游客能住满客房,
他应隔出大房间和小房间各多少间,才能获得最大收益?小结三:解答实际问题的一般步骤
(1)将已知数据列成表格形式,设出自变量x,y和目标函数z;
(2)找出约束条件及目标函数;
(3)作图,找出可行域,结合图像找出最优解,检验考虑最优解是否符合题意。特别地,对于实际问题的正整数解用网格坐标法。
表示什么图形?问题2:以二元一次不等式x+y-1>0的解为坐标点的集合
表示什么图形?1、用二元一次不等式(组)表示平面区域在平面直角坐标系中,所有的点被直线x+y-1=0分成三类:1、在直线x+y-1=0上2、在直线x+y-1=0左下方的平面区域内3、在直线x+y-1=0右上方的平面区域内0xyX+y-1>0X+y-1<011小结一:一般的,二元一次不等式Ax+By+C>0在平面坐标系中表示直线Ax+By+C=0某一侧所有点组成的区域。⒈⒉把直线画成虚线以表示区域不包括边界直线;把直线画成实线以表示区域包括边界直线;小技巧:在直线的某一侧取一个特殊点(x0,y0),代入Ax+By+C(A>0)中,
若结果为正,则这个点所在的区域表示Ax+By+C>0
若结果为负,则这个点所在的区域表示Ax+By+C<0
特殊的,当C≠0时,可以取(0,0)作为特殊点。例⒈画出不等式2x+y-6<0表示的平面区域。解:①画线:(注意虚实)②取点,作正负判断:在此取(0,0)③画出不等式表示的平面区域。36步骤:1,直线定界
2,特殊点定域⒉线性规划问题例2:基本概念:⒈z=2x+y⒊象此问题一样,求线性目标函数在线性约束条件下的最值
的问题统称为线性规划问题。小结二:对于线性目标函数z=Ax+By1、当B>0时,当直线过可行域且
在y轴上截距最大时,z的值最大,
在y轴上截距最小时,z的值最小。2、当B<0时,当直线过可行域且
在y轴上截距最大时,z的值最小,
在y轴上截距最小时,z的值最大。解线性规划问题的步骤: (2)移:设z=0,画出直线,利用平移的方法找
出与可行域有公共点且纵截距最大
或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;例3:在上题的约束条件下,的最大值和最小值是什么?解:当x=1,y=1时,有最小值为2;当x=5,y=2时,有最大值为29.例4:若P(x,y)的坐标满足上约束条件,点O为坐
标原点,则的最小值是例5:若P(x,y)的坐标满足上约束条件,的最大值是4.43、可行域上的最优解
应用例6:某人有一楼房,室内面积共180 ,
分隔两类房间作为客房。
大房间每间面积为18 ,可住5人,每人每天40元; 小房间每间面积为15 ,可住3人,住宿费每人每天50元。
装修大房间每间要1000元,装修小房间每间要600元。如果他只能筹款8000元用于装修,且游客能住满客房,
他应隔出大房间和小房间各多少间,才能获得最大收益?小结三:解答实际问题的一般步骤
(1)将已知数据列成表格形式,设出自变量x,y和目标函数z;
(2)找出约束条件及目标函数;
(3)作图,找出可行域,结合图像找出最优解,检验考虑最优解是否符合题意。特别地,对于实际问题的正整数解用网格坐标法。
