简单线性规划[上学期]
图片预览




文档简介
课件19张PPT。简单线性规划(2)遂宁高级实验中学主讲人:吴凯 深圳某搬运公司经招标承担了每天搬运至少280t水
泥的任务,已知该公司有6辆A型卡车和4辆B型卡车,
已知A型卡车每天每辆的运载量为30t,成本费为0.9
千元,B型卡车每天每辆的运载量为40t,成本费为1
千元。
如果你是公司的经理,为使公司每天所花的成本费
最少,每天应派出A型卡车、B型卡车各为多少辆?
一、创设情景,激趣诱思提出问题:
设z=2x+y, 式中的变量x、y满足下列条件
,求z的最大值和最小值
我们先对条件进行分析,再分析结论,然后再思考如何解这个题。
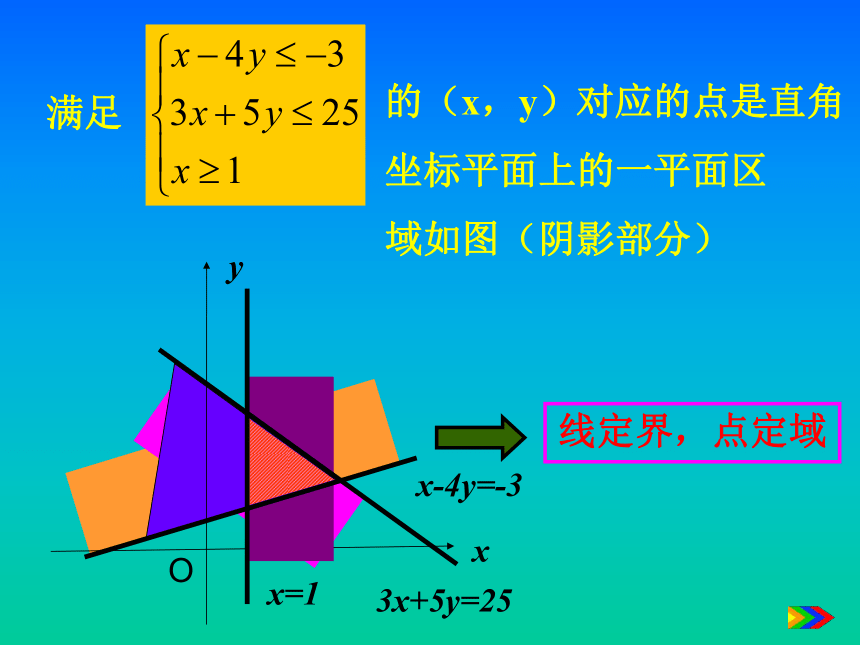
二、尝试探究,生疑释疑yxOx-4y=-33x+5y=25x=1满足的(x,y)对应的点是直角
坐标平面上的一平面区
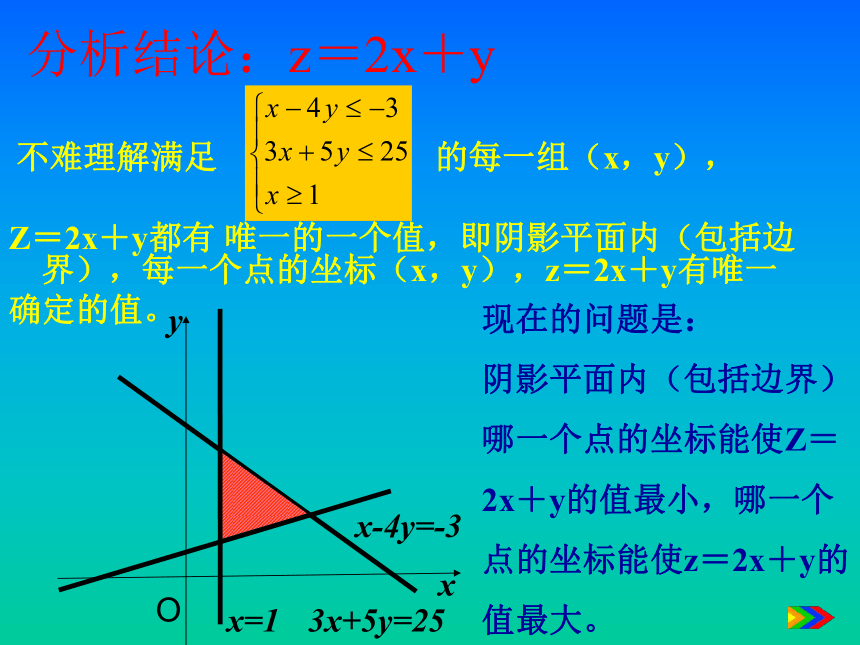
域如图(阴影部分)线定界,点定域分析结论:z=2x+y 不难理解满足 的每一组(x,y),
Z=2x+y都有 唯一的一个值,即阴影平面内(包括边界),每一个点的坐标(x,y),z=2x+y有唯一
确定的值。 y现在的问题是:
阴影平面内(包括边界)
哪一个点的坐标能使Z=
2x+y的值最小,哪一个
点的坐标能使z=2x+y的
值最大。为了便于解决好这个问题: 我们换个角度来看z=2x+y可以看出z就是直线
y=-2x+z在y轴上
的截距(z的几何意义)
因为z的不同,y=-2x
+z是一组平行线。
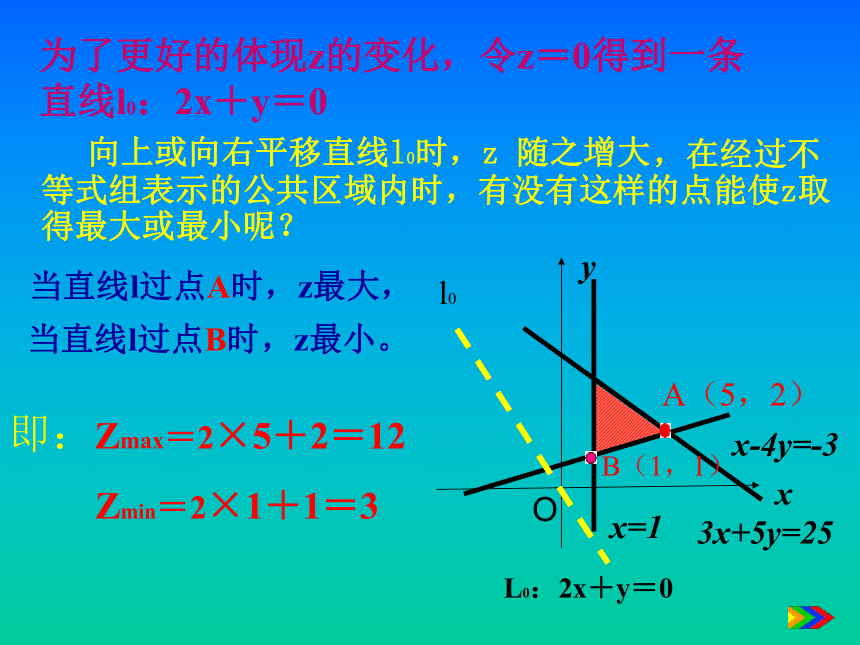
(如右图)为了更好的体现z的变化,令z=0得到一条直线l0:2x+y=0 ,在经过不等式组表示的公共区域内时,有没有这样的点能使z取得最大或最小呢?
当直线l过点B时,z最小。即:Zmax=2×5+2=12Zmin=2×1+1=3向上或向右平移直线l0时,z 随之增大L0:2x+y=0当直线l过点A时,z最大,
A(5,2)B(1,1)l0问题:设z=2x+y,式中变量满足下列条件:
求z的最大值与最小值。 目标函数
(线性目标函数)提炼概念
约束条件
( 线性约束条件)
线性规划问题 求线性目标函数在线性约束条
件下的最大值或最小值的问题
满足线性约束条件的解(x,y)
使目标函数取到最大值或最小值的可行解
可行解最优解
可行域
最优解
最优解
约束条件线性约束条件目标函数线性目标函数线性规划问题可行解可行域最优解2、有关概念请大家看书P61,勾画出相应的概念1、解线性规划问题的一般步骤:(1)画:(2)移:
(3)求:(4)答:画出线性约束条件所表示的可行域利用平移的方法在线性目标函数所表示的一组平行线 中,找出与可行域有公共点且纵截距最大或最小的直线通过解方程组求出最优解作出答案三、归纳总结、纳入系统 深圳某搬运公司经招标承担了每天搬运至少280t水
泥的任务,已知该公司有6辆A型卡车和4辆B型车,
已知A型卡车每天每辆的运载量为30t,成本费为0.9
千元,B型卡车每天每辆的运载量为40t,成本费为1
千元。
如果你是公司的经理,为使公司每天所花的成本费
最少,每天应派出A型卡车、B型卡车各为多少辆?解决问题Z =0.9x + yx=630x+40y=280答案:A型卡车4辆,
B型卡车4辆y=-0.9xA(4,4)y=4(即3x+4y=28)(y=-0.9x+z)
1、基础训练:
x、y满足约束条件:四、变式训练、形成技能求z=2x+y的最大值y=xx+y=1y=-1A(2,-1)在点A(2,-1)处z=2x+y最大
zmax=2×2+(-1)=3y=-2x求z=2x-y的最大值。
已知x、y满足如图所示2、变式训练L0:y=2x答案:在点A(5,2)处取得最大值
Zmax=2×5-2=8思考:这里z的几何意义是什么?也代表直线的众截距吗?发散:如改求
(1) 或
(2)的最大值呢? 如果z=ax+y取到最大
值的最优解有无数个,
求a的值3、创新训练已知x、y满足如下图所示y=-ax+z讨论:(1)a<0(2) a=0(3) a>0答案:1、解线性规划问题的一般步骤:(1)画(2)移(3)求(4)答2、解决线性规划问题的思想方法数形结合、化归五、总结升华、启迪创新感谢光临指导再见
泥的任务,已知该公司有6辆A型卡车和4辆B型卡车,
已知A型卡车每天每辆的运载量为30t,成本费为0.9
千元,B型卡车每天每辆的运载量为40t,成本费为1
千元。
如果你是公司的经理,为使公司每天所花的成本费
最少,每天应派出A型卡车、B型卡车各为多少辆?
一、创设情景,激趣诱思提出问题:
设z=2x+y, 式中的变量x、y满足下列条件
,求z的最大值和最小值
我们先对条件进行分析,再分析结论,然后再思考如何解这个题。
二、尝试探究,生疑释疑yxOx-4y=-33x+5y=25x=1满足的(x,y)对应的点是直角
坐标平面上的一平面区
域如图(阴影部分)线定界,点定域分析结论:z=2x+y 不难理解满足 的每一组(x,y),
Z=2x+y都有 唯一的一个值,即阴影平面内(包括边界),每一个点的坐标(x,y),z=2x+y有唯一
确定的值。 y现在的问题是:
阴影平面内(包括边界)
哪一个点的坐标能使Z=
2x+y的值最小,哪一个
点的坐标能使z=2x+y的
值最大。为了便于解决好这个问题: 我们换个角度来看z=2x+y可以看出z就是直线
y=-2x+z在y轴上
的截距(z的几何意义)
因为z的不同,y=-2x
+z是一组平行线。
(如右图)为了更好的体现z的变化,令z=0得到一条直线l0:2x+y=0 ,在经过不等式组表示的公共区域内时,有没有这样的点能使z取得最大或最小呢?
当直线l过点B时,z最小。即:Zmax=2×5+2=12Zmin=2×1+1=3向上或向右平移直线l0时,z 随之增大L0:2x+y=0当直线l过点A时,z最大,
A(5,2)B(1,1)l0问题:设z=2x+y,式中变量满足下列条件:
求z的最大值与最小值。 目标函数
(线性目标函数)提炼概念
约束条件
( 线性约束条件)
线性规划问题 求线性目标函数在线性约束条
件下的最大值或最小值的问题
满足线性约束条件的解(x,y)
使目标函数取到最大值或最小值的可行解
可行解最优解
可行域
最优解
最优解
约束条件线性约束条件目标函数线性目标函数线性规划问题可行解可行域最优解2、有关概念请大家看书P61,勾画出相应的概念1、解线性规划问题的一般步骤:(1)画:(2)移:
(3)求:(4)答:画出线性约束条件所表示的可行域利用平移的方法在线性目标函数所表示的一组平行线 中,找出与可行域有公共点且纵截距最大或最小的直线通过解方程组求出最优解作出答案三、归纳总结、纳入系统 深圳某搬运公司经招标承担了每天搬运至少280t水
泥的任务,已知该公司有6辆A型卡车和4辆B型车,
已知A型卡车每天每辆的运载量为30t,成本费为0.9
千元,B型卡车每天每辆的运载量为40t,成本费为1
千元。
如果你是公司的经理,为使公司每天所花的成本费
最少,每天应派出A型卡车、B型卡车各为多少辆?解决问题Z =0.9x + yx=630x+40y=280答案:A型卡车4辆,
B型卡车4辆y=-0.9xA(4,4)y=4(即3x+4y=28)(y=-0.9x+z)
1、基础训练:
x、y满足约束条件:四、变式训练、形成技能求z=2x+y的最大值y=xx+y=1y=-1A(2,-1)在点A(2,-1)处z=2x+y最大
zmax=2×2+(-1)=3y=-2x求z=2x-y的最大值。
已知x、y满足如图所示2、变式训练L0:y=2x答案:在点A(5,2)处取得最大值
Zmax=2×5-2=8思考:这里z的几何意义是什么?也代表直线的众截距吗?发散:如改求
(1) 或
(2)的最大值呢? 如果z=ax+y取到最大
值的最优解有无数个,
求a的值3、创新训练已知x、y满足如下图所示y=-ax+z讨论:(1)a<0(2) a=0(3) a>0答案:1、解线性规划问题的一般步骤:(1)画(2)移(3)求(4)答2、解决线性规划问题的思想方法数形结合、化归五、总结升华、启迪创新感谢光临指导再见
