9.2.2 多边形的外角和 教案
图片预览


文档简介
中小学教育资源及组卷应用平台
9.2.2多边形的外角和 教学设计
课题 9.2.2多边形的外角和 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 了解多边形的内角、外角、对角线等概念.在熟悉和掌握多边形内角和定理的基础上,推理并掌握多边形的外角和定理.
核心素养分析 经历质疑、猜想、归纳等活动,发展学生的推理能力,积累数学活动的经验,在探索中学会与人合作,学会和别人交流自己的思想和方法.
学习目标 1、了解多边形的外角定义,并能准确找出多边形的外角 .2、掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题.
重点 多边形的外角和公式及其应用.
难点 多边形的外角和公式的应用.
教学过程
教学环节 教师活动 学生活动 设计意图
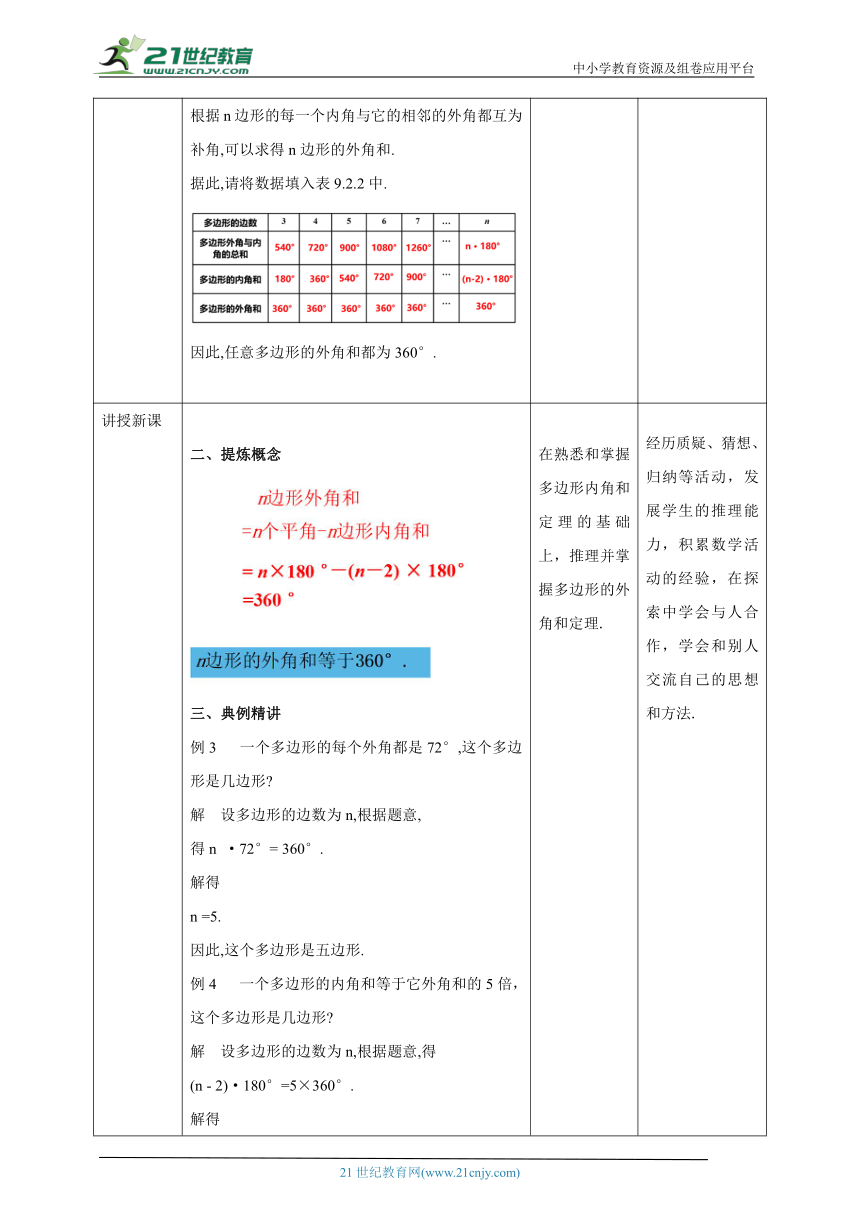
导入新课 一、创设情景,引出课题回顾:n边形的内角和公式是什么?n边形的内角和为(n -2) ·180°它有什么作用呢 1.知道多边形的边数,可以求出多边形的度数.2.知道多边形的度数,可以求出多边形的边数.探究一:问题1多边形有没有外角?有没有外角和?若有外角?有多少个外角?请以下图为例,说说看.思考1.什么样的角时多边形的外角?2.怎样的角的和才算是多边形的外角和呢?多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角,他们的和叫做这个多边形的外角和.与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.如图9.2.6,∠1+∠2+∠3+∠4就是四边形ABCD的外角和.从图中可以知道:(∠1 +∠5)+(∠2 +∠6) +(∠3+∠7)+(∠4 +∠8 ) = 4 x180°,所以∠1 +∠2+∠3 +∠4= 4 × 180°-(∠5+∠6 +∠7+∠8).四边形ABCD的内角和为∠5+∠6+∠7+∠8=360°.因此∠1+∠2+∠3+∠4= 360°.那么,n边形的外角和应该等于多少度呢 探究二:探索根据n边形的每一个内角与它的相邻的外角都互为补角,可以求得n边形的外角和.据此,请将数据填入表9.2.2中.因此,任意多边形的外角和都为360°. 思考自议以问题导入,吸引学生注意力,导入本节多边形的外角和. 引入新课,激发学生探究多边形的外角和的兴趣.
讲授新课 二、提炼概念三、典例精讲例3 一个多边形的每个外角都是72°,这个多边形是几边形 解 设多边形的边数为n,根据题意,得n ·72°= 360°.解得n =5.因此,这个多边形是五边形.例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形 解 设多边形的边数为n,根据题意,得(n - 2)·180°=5×360°.解得n=12.因此,这个多边形是十二边形. 在熟悉和掌握多边形内角和定理的基础上,推理并掌握多边形的外角和定理. 经历质疑、猜想、归纳等活动,发展学生的推理能力,积累数学活动的经验,在探索中学会与人合作,学会和别人交流自己的思想和方法.
课堂练习 四、巩固训练1. 一个多边形的外角和是360°,这个多边形是( )A. 四边形 B. 五边形 C. 六边形 D. 不确定 D2、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A. 8 B. 9 C. 10 D. 11A3.如图所示,小华从A点出发,沿直线前进10 m后左转24°,再沿直线前进10m,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是 .1504.一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.解:设该正多边形的内角是x°,外角是y°,则得到一个方程组 解得而任何多边形的外角和是360°,则该正多边形的边数为360÷120=3,故这个多边形的每个内角的度数是60°,边数是三条.5.已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.解:设这个多边形的内角为7x °,外角为2x°,根据题意得7x+2x=180,解得x=20.即每个内角是140 °,每个外角是40 °.360° ÷40 °=9.答:这个多边形是九边形.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
9.2.2多边形的外角和 教学设计
课题 9.2.2多边形的外角和 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 了解多边形的内角、外角、对角线等概念.在熟悉和掌握多边形内角和定理的基础上,推理并掌握多边形的外角和定理.
核心素养分析 经历质疑、猜想、归纳等活动,发展学生的推理能力,积累数学活动的经验,在探索中学会与人合作,学会和别人交流自己的思想和方法.
学习目标 1、了解多边形的外角定义,并能准确找出多边形的外角 .2、掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题.
重点 多边形的外角和公式及其应用.
难点 多边形的外角和公式的应用.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题回顾:n边形的内角和公式是什么?n边形的内角和为(n -2) ·180°它有什么作用呢 1.知道多边形的边数,可以求出多边形的度数.2.知道多边形的度数,可以求出多边形的边数.探究一:问题1多边形有没有外角?有没有外角和?若有外角?有多少个外角?请以下图为例,说说看.思考1.什么样的角时多边形的外角?2.怎样的角的和才算是多边形的外角和呢?多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角,他们的和叫做这个多边形的外角和.与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.如图9.2.6,∠1+∠2+∠3+∠4就是四边形ABCD的外角和.从图中可以知道:(∠1 +∠5)+(∠2 +∠6) +(∠3+∠7)+(∠4 +∠8 ) = 4 x180°,所以∠1 +∠2+∠3 +∠4= 4 × 180°-(∠5+∠6 +∠7+∠8).四边形ABCD的内角和为∠5+∠6+∠7+∠8=360°.因此∠1+∠2+∠3+∠4= 360°.那么,n边形的外角和应该等于多少度呢 探究二:探索根据n边形的每一个内角与它的相邻的外角都互为补角,可以求得n边形的外角和.据此,请将数据填入表9.2.2中.因此,任意多边形的外角和都为360°. 思考自议以问题导入,吸引学生注意力,导入本节多边形的外角和. 引入新课,激发学生探究多边形的外角和的兴趣.
讲授新课 二、提炼概念三、典例精讲例3 一个多边形的每个外角都是72°,这个多边形是几边形 解 设多边形的边数为n,根据题意,得n ·72°= 360°.解得n =5.因此,这个多边形是五边形.例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形 解 设多边形的边数为n,根据题意,得(n - 2)·180°=5×360°.解得n=12.因此,这个多边形是十二边形. 在熟悉和掌握多边形内角和定理的基础上,推理并掌握多边形的外角和定理. 经历质疑、猜想、归纳等活动,发展学生的推理能力,积累数学活动的经验,在探索中学会与人合作,学会和别人交流自己的思想和方法.
课堂练习 四、巩固训练1. 一个多边形的外角和是360°,这个多边形是( )A. 四边形 B. 五边形 C. 六边形 D. 不确定 D2、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A. 8 B. 9 C. 10 D. 11A3.如图所示,小华从A点出发,沿直线前进10 m后左转24°,再沿直线前进10m,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是 .1504.一个正多边形的一个外角比一个内角大60°,求这个多边形的每个内角的度数及边数.解:设该正多边形的内角是x°,外角是y°,则得到一个方程组 解得而任何多边形的外角和是360°,则该正多边形的边数为360÷120=3,故这个多边形的每个内角的度数是60°,边数是三条.5.已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.解:设这个多边形的内角为7x °,外角为2x°,根据题意得7x+2x=180,解得x=20.即每个内角是140 °,每个外角是40 °.360° ÷40 °=9.答:这个多边形是九边形.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
