人教版八年级下册18.2特殊的平行四边形培优练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2特殊的平行四边形培优练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 694.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 07:25:13 | ||
图片预览


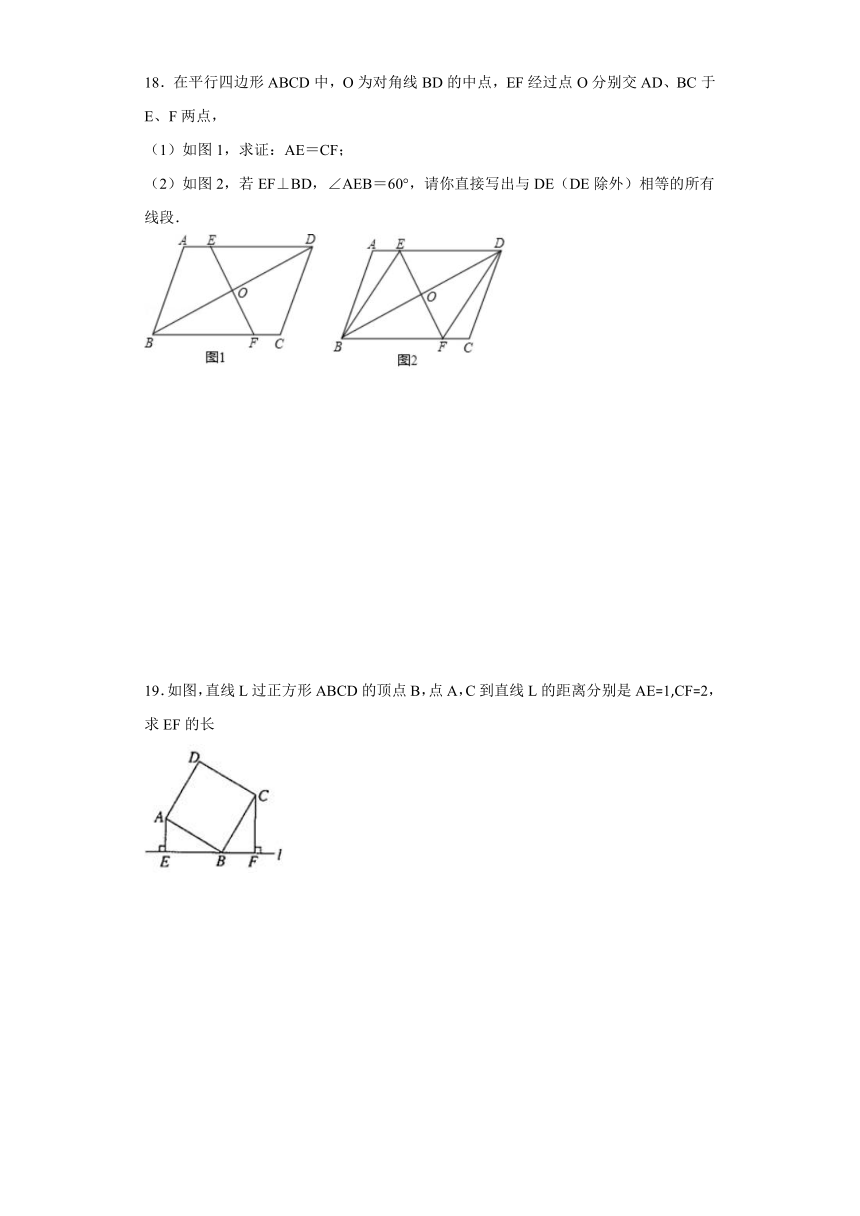
文档简介
18.2特殊的平行四边形 培优练习
一、单选题
1.已知矩形的对角线长为10,那么顺次连接矩形四边中点所得的四边形的周长为( )
A.40 B.10 C.20 D.5
2.若顺次连接四边形ABCD各边中点所得的四边形是菱形,则下列结论中正确的是( )
A.AB∥CD B.AB⊥BC C.AC⊥BD D.AC=BD
3.如图,把一个长方形纸片对折两次,然后沿图中虚线剪下一个角,为了得到一个内角为100°的菱形,剪切线与折痕所成的角的大小等于( )
A.80° B.60° C.40° D.20°
4.下列命题中,真命题的是( )
A.两组对角相等的四边形是平行四边形 B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.对角线互相垂直平分的四边形是正方形
5.如图,四边形中,,,.若,则的最大值是( )
A. B. C. D.
6.如图,,,点在边上与、不重合,四边形为正方形,过点作,交的延长线于点,连接,交于点.给出以下结论:①≌;②;③:2;④其中正确结论的个数是( )
A. B. C. D.
7.如图,在△ABC中,∠ACB=90°,D为AB边的中点,连接CD并延长至点E,使DE=CD.连接AE,过点B作BF∥DE交AE的延长线于点F,若BF=7,则AB的长为( )
A.3.5 B.7 C.10 D.14
8.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.六边形内角和为
C.的平方根是
D.对角线相等的平行四边形是矩形
9.已知:如图,中,,点是射线上一动点,以为一边向左画正方形.连接,取中点,则的最小值为( )
A.2 B. C.4 D.
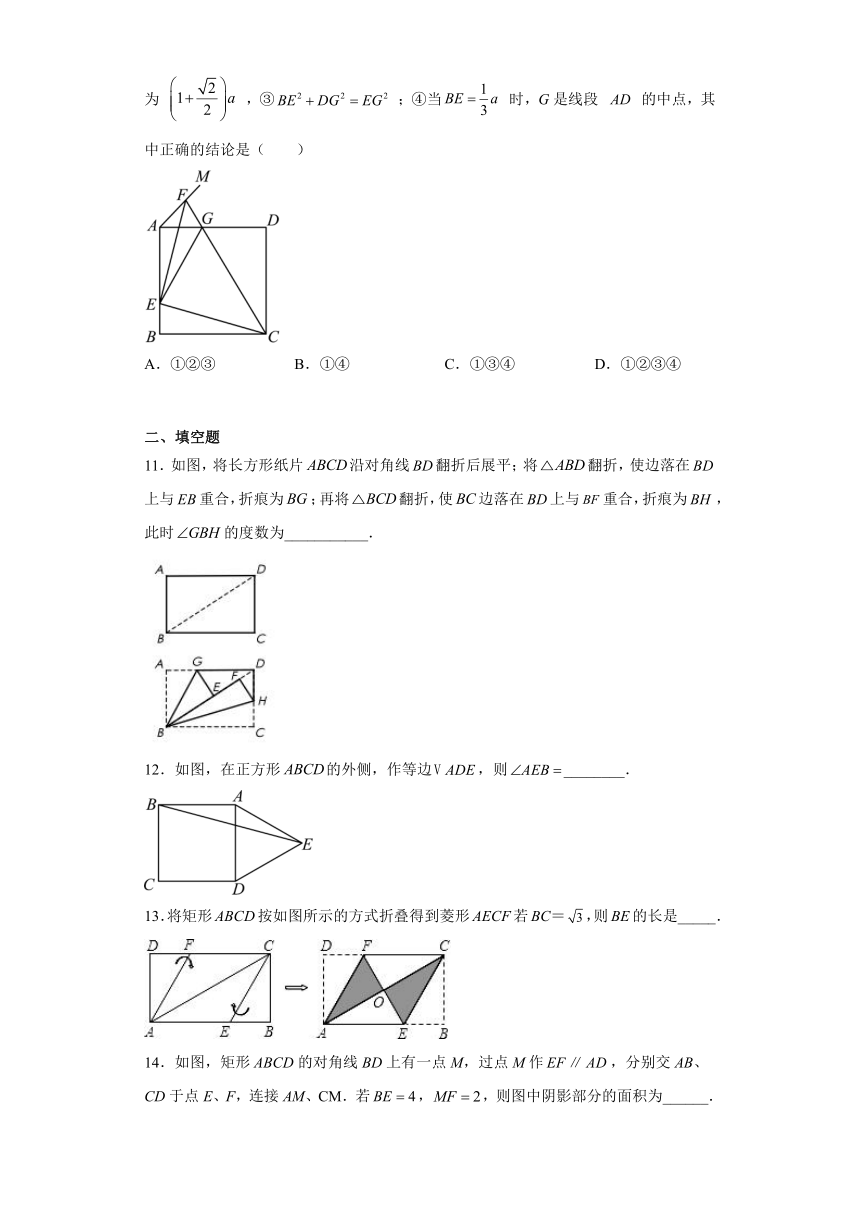
10.如图,正方形 的边长为a,点E在边 上运动(不与点A,B重合), ,点F在射线 上,且 与 相交于点G,连接 .则下列结论:① ,② 的周长为 ,③ ;④当 时,G是线段 的中点,其中正确的结论是( )
A.①②③ B.①④ C.①③④ D.①②③④
二、填空题
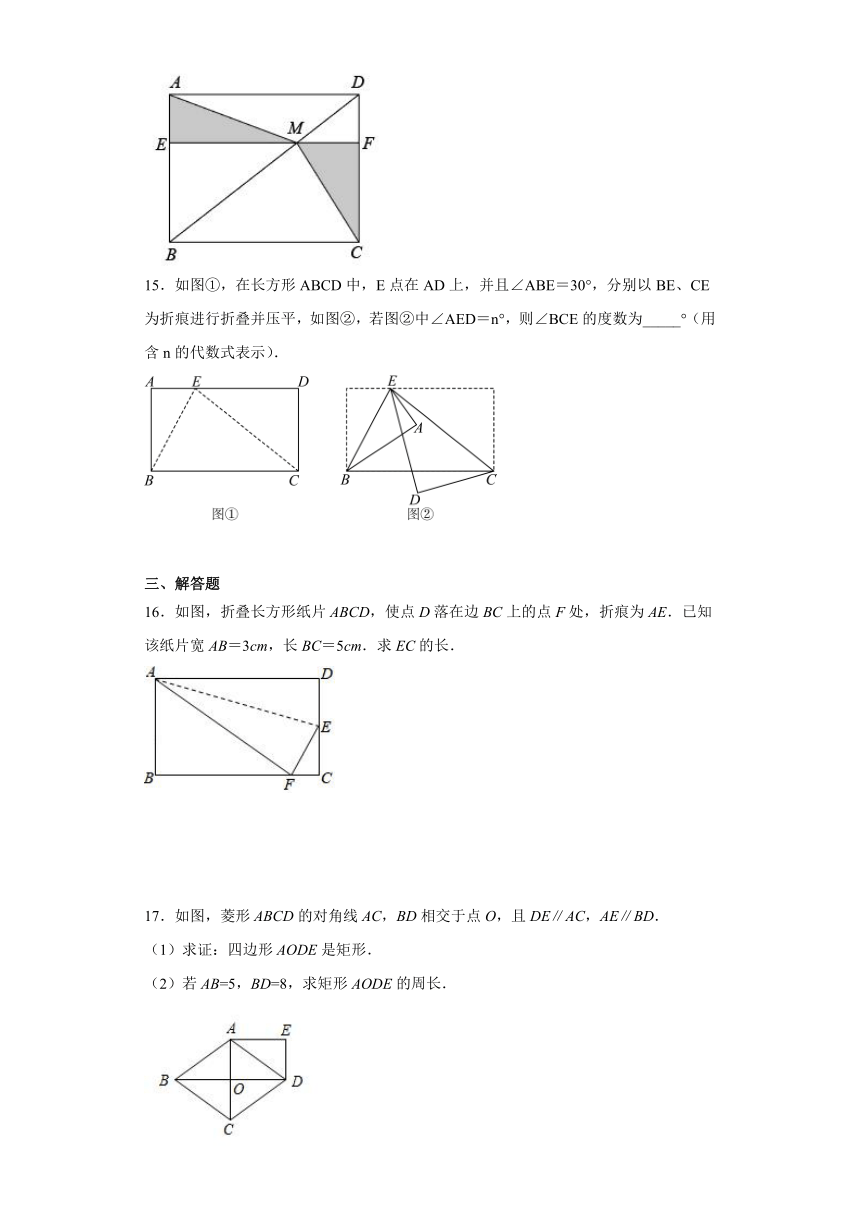
11.如图,将长方形纸片沿对角线翻折后展平;将翻折,使边落在上与重合,折痕为;再将翻折,使边落在上与重合,折痕为,此时的度数为___________.
12.如图,在正方形的外侧,作等边,则________.
13.将矩形ABCD按如图所示的方式折叠得到菱形AECF若BC=,则BE的长是_____.
14.如图,矩形ABCD的对角线BD上有一点M,过点M作,分别交AB、CD于点E、F,连接AM、CM.若,,则图中阴影部分的面积为______.
15.如图①,在长方形ABCD中,E点在AD上,并且∠ABE=30°,分别以BE、CE为折痕进行折叠并压平,如图②,若图②中∠AED=n°,则∠BCE的度数为_____°(用含n的代数式表示).
三、解答题
16.如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知该纸片宽AB=3cm,长BC=5cm.求EC的长.
17.如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.
18.在平行四边形ABCD中,O为对角线BD的中点,EF经过点O分别交AD、BC于E、F两点,
(1)如图1,求证:AE=CF;
(2)如图2,若EF⊥BD,∠AEB=60°,请你直接写出与DE(DE除外)相等的所有线段.
19.如图,直线L过正方形ABCD的顶点B,点A,C到直线L的距离分别是AE=1,CF=2,求EF的长
20.如图,四边形是正方形,点是线段的延长线上一点,点是线段上一点,连接,以点为直角顶点作交的角平分线于,过点作交于,连接,,.
(1)求证:.
(2)求证:.
(3)若,,求的长.
参考答案
1.C
2.D
3.C
4.A
5.A
6.D
7.B
8.D
9.B
10.B
11.45°
12.15°/15度
13.1
14.8
15.
16.解:由折叠可知AD=AF=5cm,DE=EF
∵∠B=90°
∴AB2+BF2=AF2,
∵AB=3cm,AF=5cm
∴BF=4cm,
∵BC=5cm,
∴FC=1cm
∵∠C=90°,
∴EC2+FC2=EF2
设EC=x,则DE=EF=3﹣x
∴(3﹣x)2=12+x2
∴x=
即EC=.
17.(1)证明:∵四边形ABCD是菱形,
∴∠AOD=90°.
又∵DE//AC,AE//BD,
∴四边形AODE是平行四边形.
∴四边形AODE是矩形.
(2)∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD=BD=×8=4.
在Rt△AOB中,.
在矩形AODE中,
DE=OA=3,AE=OD=4,
∴ OA+OD+DE+AE=14
即矩形AODE的周长为14.
18.(1)证明:四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
AD//BC,AD=BC,OB=OD.
∠OED=∠OFB, ∠EDO=∠FBO.
在△EOD与△FOB中,,
△EOD≌△FOB
ED=BF,
又 AD=BC
AE=CF.
(2)由(1)得△EOD≌△FOB
OE=OF,
由OB=OD,EF⊥BD
四边形BFDE为菱形,
∠AEB=60°,∠BED=120°,且四边形BFDE为菱形,
∠BEF=∠DEF=60°, △BEF与△BEF为等边三角形,
与DE相等的所有线段为:BE、BF、EF、DF.
19.解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥BE,CF⊥BF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
∴△ABE≌△BCF(ASA),
∴BE=CF=2,AE=BF=1,
∴EF=BE+BF=3.
20.(1)证明:在边上截取线段,使连.
∵四边形是正方形
;
∵BN平分
在中,,
在和中
∴
.
(2)如图,
设与CE的交点为H,
∵四边形是正方形
∴
∵
在和中,
∴.
又,
又.
四边形为平行四边形.
.
(3)解:如图所示,过作垂足为.
由(2)知,
,
又
∴即
平分所以,
∴三角形是等腰直角三角形,
在中,
设,则,即,
.
,,
在中,,
又在中,,,
.
一、单选题
1.已知矩形的对角线长为10,那么顺次连接矩形四边中点所得的四边形的周长为( )
A.40 B.10 C.20 D.5
2.若顺次连接四边形ABCD各边中点所得的四边形是菱形,则下列结论中正确的是( )
A.AB∥CD B.AB⊥BC C.AC⊥BD D.AC=BD
3.如图,把一个长方形纸片对折两次,然后沿图中虚线剪下一个角,为了得到一个内角为100°的菱形,剪切线与折痕所成的角的大小等于( )
A.80° B.60° C.40° D.20°
4.下列命题中,真命题的是( )
A.两组对角相等的四边形是平行四边形 B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.对角线互相垂直平分的四边形是正方形
5.如图,四边形中,,,.若,则的最大值是( )
A. B. C. D.
6.如图,,,点在边上与、不重合,四边形为正方形,过点作,交的延长线于点,连接,交于点.给出以下结论:①≌;②;③:2;④其中正确结论的个数是( )
A. B. C. D.
7.如图,在△ABC中,∠ACB=90°,D为AB边的中点,连接CD并延长至点E,使DE=CD.连接AE,过点B作BF∥DE交AE的延长线于点F,若BF=7,则AB的长为( )
A.3.5 B.7 C.10 D.14
8.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.六边形内角和为
C.的平方根是
D.对角线相等的平行四边形是矩形
9.已知:如图,中,,点是射线上一动点,以为一边向左画正方形.连接,取中点,则的最小值为( )
A.2 B. C.4 D.
10.如图,正方形 的边长为a,点E在边 上运动(不与点A,B重合), ,点F在射线 上,且 与 相交于点G,连接 .则下列结论:① ,② 的周长为 ,③ ;④当 时,G是线段 的中点,其中正确的结论是( )
A.①②③ B.①④ C.①③④ D.①②③④
二、填空题
11.如图,将长方形纸片沿对角线翻折后展平;将翻折,使边落在上与重合,折痕为;再将翻折,使边落在上与重合,折痕为,此时的度数为___________.
12.如图,在正方形的外侧,作等边,则________.
13.将矩形ABCD按如图所示的方式折叠得到菱形AECF若BC=,则BE的长是_____.
14.如图,矩形ABCD的对角线BD上有一点M,过点M作,分别交AB、CD于点E、F,连接AM、CM.若,,则图中阴影部分的面积为______.
15.如图①,在长方形ABCD中,E点在AD上,并且∠ABE=30°,分别以BE、CE为折痕进行折叠并压平,如图②,若图②中∠AED=n°,则∠BCE的度数为_____°(用含n的代数式表示).
三、解答题
16.如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知该纸片宽AB=3cm,长BC=5cm.求EC的长.
17.如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.
18.在平行四边形ABCD中,O为对角线BD的中点,EF经过点O分别交AD、BC于E、F两点,
(1)如图1,求证:AE=CF;
(2)如图2,若EF⊥BD,∠AEB=60°,请你直接写出与DE(DE除外)相等的所有线段.
19.如图,直线L过正方形ABCD的顶点B,点A,C到直线L的距离分别是AE=1,CF=2,求EF的长
20.如图,四边形是正方形,点是线段的延长线上一点,点是线段上一点,连接,以点为直角顶点作交的角平分线于,过点作交于,连接,,.
(1)求证:.
(2)求证:.
(3)若,,求的长.
参考答案
1.C
2.D
3.C
4.A
5.A
6.D
7.B
8.D
9.B
10.B
11.45°
12.15°/15度
13.1
14.8
15.
16.解:由折叠可知AD=AF=5cm,DE=EF
∵∠B=90°
∴AB2+BF2=AF2,
∵AB=3cm,AF=5cm
∴BF=4cm,
∵BC=5cm,
∴FC=1cm
∵∠C=90°,
∴EC2+FC2=EF2
设EC=x,则DE=EF=3﹣x
∴(3﹣x)2=12+x2
∴x=
即EC=.
17.(1)证明:∵四边形ABCD是菱形,
∴∠AOD=90°.
又∵DE//AC,AE//BD,
∴四边形AODE是平行四边形.
∴四边形AODE是矩形.
(2)∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD=BD=×8=4.
在Rt△AOB中,.
在矩形AODE中,
DE=OA=3,AE=OD=4,
∴ OA+OD+DE+AE=14
即矩形AODE的周长为14.
18.(1)证明:四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
AD//BC,AD=BC,OB=OD.
∠OED=∠OFB, ∠EDO=∠FBO.
在△EOD与△FOB中,,
△EOD≌△FOB
ED=BF,
又 AD=BC
AE=CF.
(2)由(1)得△EOD≌△FOB
OE=OF,
由OB=OD,EF⊥BD
四边形BFDE为菱形,
∠AEB=60°,∠BED=120°,且四边形BFDE为菱形,
∠BEF=∠DEF=60°, △BEF与△BEF为等边三角形,
与DE相等的所有线段为:BE、BF、EF、DF.
19.解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥BE,CF⊥BF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
∴△ABE≌△BCF(ASA),
∴BE=CF=2,AE=BF=1,
∴EF=BE+BF=3.
20.(1)证明:在边上截取线段,使连.
∵四边形是正方形
;
∵BN平分
在中,,
在和中
∴
.
(2)如图,
设与CE的交点为H,
∵四边形是正方形
∴
∵
在和中,
∴.
又,
又.
四边形为平行四边形.
.
(3)解:如图所示,过作垂足为.
由(2)知,
,
又
∴即
平分所以,
∴三角形是等腰直角三角形,
在中,
设,则,即,
.
,,
在中,,
又在中,,,
.
