18章平行四边形小结与复习 课件(共27张PPT)
文档属性
| 名称 | 18章平行四边形小结与复习 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 18:12:48 | ||
图片预览






文档简介
(共27张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
小结与复习
建立平行四边形及特殊平行四边形的知识框架,掌握平行四边形及特殊平行四边形的判定,并能熟练应用.
核心素养目标:
通过对几种平行四边形的回顾和思考,使学生梳理所学的知识,系统地复习平行四边形与各种特殊平行四边形的定义,性质,判定方法,正确理解平行四边形与各种特殊平行四边形的联系与区别.
本章我们主要学行四边形的性质定理、判定定理;探索并证明了三角形的中位线定理,介绍了平行线问距离的概念;通过平行四边形边、角的特殊化,获得了特殊的平行四边形——矩形、菱形和正方形,了解了它们之间的关系;根据它们的特殊性,得到了这些特殊的平行四边形的性质定理和判定定理.
在学习这些知识的过程中,我们采用了从一般到特殊的研究方法:利用图形的性质定理与判定定理之间的关系,通过证明性质定理的逆命题,得到了图形的判定定理,这些方法在今后的学习中都是很有用的.
回顾与思考:
1,你能概述一下研究平行四边形的思路和方法吗
2.平行四边形有哪些性质 如何判定一个四边形是平行四边形
3.矩形、菱形、正方形除了具有平行四边形的性质外,分别还具有哪些性质 如何判定一个四边形是矩形、菱形、正方形 你能总结一下研究这些性质和判定的方法吗
4.本章我们利用平行四边形的性质,得出了三角形的中位线定理,你能仿照这一过程,再得出一些其他几何结论吗
回顾与思考:
请你带着下面的问题,复习一下全章的内容吧。
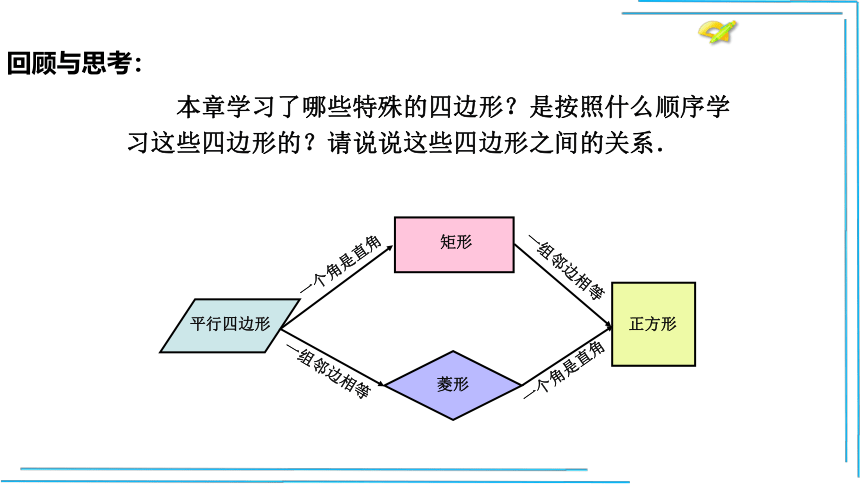
本章学习了哪些特殊的四边形?是按照什么顺序学
习这些四边形的?请说说这些四边形之间的关系.
一个角是直角
一组邻边相等
平行四边形
矩形
菱形
一组邻边相等
一个角是直角
正方形
回顾与思考:
研究内容
研究步骤
研究方法
平行四
边形
矩形
菱形
正方形
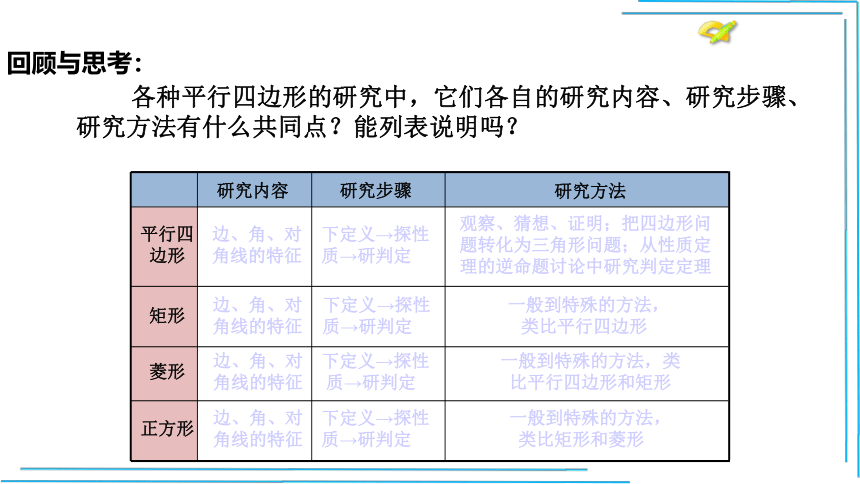
各种平行四边形的研究中,它们各自的研究内容、研究步骤、研究方法有什么共同点?能列表说明吗?
边、角、对
角线的特征
下定义→探性 质→研判定
观察、猜想、证明;把四边形问
题转化为三角形问题;从性质定
理的逆命题讨论中研究判定定理
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比平行四边形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,类
比平行四边形和矩形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比矩形和菱形
回顾与思考:
这是研究图形的基本思路.
(1)本章研究内容:各种平行四边形的边、角、对角
线的特征;
(2)研究步骤:下定义→探性质→研判定;
(3)研究方法:观察、猜想、证明;建立当前图形
(平行四边形)与三角形的联系;从性质定理的
逆命题的讨论中研究判定定理;类比、一般到特
殊.
回顾与思考:
一、几种特殊四边形的性质
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
知识梳理:
四边形 条件
平行 四边形
矩形
菱形
正方形
二、几种特殊四边形的常用判定方法:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形
2.对角线互相垂直的平行四边形
3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
知识梳理:
矩形
菱形
正方形
平行四边形
四边形
知识梳理:
三、平行四边形、矩形、菱形、正方形之间的关系
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
三、平行四边形、矩形、菱形、正方形之间的关系
知识梳理:
1.两条平行线之间的距离:
2.三角形的中位线定理:
两条平行线中,一条直线上任意一点到另一条直线的距
离叫做两条平行线之间的距离.
三角形的中位线平行于第三边,并且等于第三边的一半
3.直角三角形斜边上的中线:
直角三角形斜边上的中线等于斜边的一半.
四、其他重要概念
知识梳理:
考题分类:
[考点一]:平行四边形的性质与判定
例1 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)求证:四边形DEGF是平行四边形;
(2)如果点G是BC的中点,且BC=12,CD=10,求四边形AGCD的面积.
(1)证明:∵ AG∥CD,AD∥BC
∴ 四边形AGCD是平行四边形 ∴ AG=CD
∵ E、F分别为AG、CD的中点∴ EG=AG,DF=CD
∴ EG=DF且EG∥DF∴ 四边形DEGF是平行四边形
(2)解:∵ 点G是BC的中点,BC=12∴ BG=CG=BC=6
∵ 四边形AGCD是平行四边形∴ AG=CD=10
在Rt△ABG中,根据勾股定理AB===8∴ S四边形AGCD=6×8=48
考题分类:
[考点一]:平行四边形的性质与判定
例2 如图,在□ABCD中,点E在边BC上,点F在边DA的延长线上,且AF=CE,EF与AB交于点G.
(1)求证:AC∥EF;
(2)若点G是AB的中点,BE=6,求边AD的长.
(1)证明:∵ 四边形ABCD是平行四边形
∴ AD∥BC ∴ AF∥CE
又∵ AF=CE
∴ 四边形AFEC是平行四边形∴ AC∥EF
(2)解:∵ AD∥BC,∴ ∠F=∠BEG,∠FAG=∠B
∵ 点G是AB的中点,∴ AG=BG
∴ △AGF≌△BGE (AAS)∴ AF=BE=6
∴ CE=AF=6 ∴ BC=BE+CE=12
∵ 四边形ABCD是平行四边形∴ AD=BC=12
考题分类:
[考点二]:三角形的中位线与Rt△斜边上的中线
例3 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
证明:(1)∵ 点D,E,F分别是AB,BC,CA的中点
∴ DE、EF都是△ABC的中位线∴ DE∥AC,EF∥AB
∴ 四边形ADEF是平行四边形
(2)∵ 四边形ADEF是平行四边形
∴ ∠DEF=∠BAC
∵ D,F分别是AB,CA的中点,AH是边BC上的高
∴ DH、FH分别是Rt△ABH和Rt△ACH斜边上的中线
∴ DH=AD,FH=AF∴ ∠DAH=∠DHA,∠FAH=∠FHA
∵ ∠DAH+∠FAH=∠BAC ;∠DHA+∠FHA=∠DHF
∴ ∠DHF=∠BAC∴ ∠DHF=∠DEF
考题分类:
[考点三]:特殊平行四边形的性质与判定
例4 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作DE∥AC,两线相交于点E.
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥DE于点E,求∠AOD的度数.
(1)证明:∵ AE∥BD,DE∥AC∴ 四边形AODE是平行四边形
∵ 四边形ABCD是矩形∴ AC=BD,OA=AC,OD=BD
∴ OA=OD∴ 四边形AODE是菱形
(2)解:连接OE.
由(1)得,四边形AODE是菱形,∴ AE=AO=BO
∵ AE∥BO,∴ 四边形AEOB是平行四边形
∵ BE⊥DE,DE∥AC,∴ BE⊥AO
∴ 四边形AEOB是菱形∴ AE=AB=BO
∴ AB=BO=AO∴ △AOB是等边三角形
∴ ∠AOB=60°∴ ∠AOD=180°-60°=120°
考题分类:
[考点三]:特殊平行四边形的性质与判定
例5 如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.理由如下:
∵ EF垂直平分BC,∴ BF=CF,BE=CE
∴ ∠3=∠1
∵ ∠ACB=90°,∴ ∠3+∠A=90°,∠1+∠2=90°
∴ ∠2=∠A,∴ CE=AE
∴ BE=AE
∵ CF=AE
∴ BE=CE=CF=BF
∴ 四边形BECF是菱形
考题分类:
[考点三]:特殊平行四边形的性质与判定
例5 如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(2)当∠A=45°时,四边形BECF是正方形.
证明:∵ ∠A=45°,∠ACB=90°
∴ ∠CBA=45°
∵ 四边形BECF是菱形
∴ ∠EBF=2∠CBA=90°
∴ 菱形BECF是正方形
方法总结
正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个菱形有一个角为直角;
③还可以先判定四边形是平行四边形,再用①或②进行判定.
例6 在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少.
解:如图,∵在平行四边形ABCD中,AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE.
又∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE.
(1)当AE=2时,则平行四边形的周长=2×(2+5)=14.
(2)当AE=3时,则平行四边形的周长=2×(3+5)=16.
本章思想方法:
一、分类讨论思想
例7 如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:
(1)FC的长;
(2)EF的长.
解:(1)由题意得AF=AD=10cm,
在Rt△ABF中,∵AB=8,
∴BF=6cm,
∴FC=BC-BF=10-6=4(cm).
(2)由题意可得EF=DE,可设DE的长为x,
在Rt△EFC中,(8-x)2+42=x2,
解得x=5,
即EF的长为5cm.
本章思想方法:
二、方程思想
例8 如图,平行四边形ABCD中,AC、BD为对角线,其交点为O,若BC=6,BC边上的高为4,试求阴影部分的面积.
解:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵AB∥CD,
∴∠EAO=∠HCO.
又∵ ∠AOE=∠COH,
∴△AEO≌△CHO(ASA),
同理可得△OAQ≌△OCG,△OPD≌△OFB,
∴S阴影=S△BCD= S平行四边形ABCD= ×6×4=12.
Q
G
E
H
F
P
本章思想方法:
三、转化思想
四边形
两组对边
分别平行
平行四边形
矩形
菱形
正方形
一个角是直角
一组邻
边相等
一组邻边相等
一个角
是直角
课堂小结:
课后作业:
必做题:教科书第67页复习题18第1,2,4,6,7,9,12题;
选做题:教科书第69页复习题18第14题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
小结与复习
建立平行四边形及特殊平行四边形的知识框架,掌握平行四边形及特殊平行四边形的判定,并能熟练应用.
核心素养目标:
通过对几种平行四边形的回顾和思考,使学生梳理所学的知识,系统地复习平行四边形与各种特殊平行四边形的定义,性质,判定方法,正确理解平行四边形与各种特殊平行四边形的联系与区别.
本章我们主要学行四边形的性质定理、判定定理;探索并证明了三角形的中位线定理,介绍了平行线问距离的概念;通过平行四边形边、角的特殊化,获得了特殊的平行四边形——矩形、菱形和正方形,了解了它们之间的关系;根据它们的特殊性,得到了这些特殊的平行四边形的性质定理和判定定理.
在学习这些知识的过程中,我们采用了从一般到特殊的研究方法:利用图形的性质定理与判定定理之间的关系,通过证明性质定理的逆命题,得到了图形的判定定理,这些方法在今后的学习中都是很有用的.
回顾与思考:
1,你能概述一下研究平行四边形的思路和方法吗
2.平行四边形有哪些性质 如何判定一个四边形是平行四边形
3.矩形、菱形、正方形除了具有平行四边形的性质外,分别还具有哪些性质 如何判定一个四边形是矩形、菱形、正方形 你能总结一下研究这些性质和判定的方法吗
4.本章我们利用平行四边形的性质,得出了三角形的中位线定理,你能仿照这一过程,再得出一些其他几何结论吗
回顾与思考:
请你带着下面的问题,复习一下全章的内容吧。
本章学习了哪些特殊的四边形?是按照什么顺序学
习这些四边形的?请说说这些四边形之间的关系.
一个角是直角
一组邻边相等
平行四边形
矩形
菱形
一组邻边相等
一个角是直角
正方形
回顾与思考:
研究内容
研究步骤
研究方法
平行四
边形
矩形
菱形
正方形
各种平行四边形的研究中,它们各自的研究内容、研究步骤、研究方法有什么共同点?能列表说明吗?
边、角、对
角线的特征
下定义→探性 质→研判定
观察、猜想、证明;把四边形问
题转化为三角形问题;从性质定
理的逆命题讨论中研究判定定理
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比平行四边形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,类
比平行四边形和矩形
边、角、对
角线的特征
下定义→探性
质→研判定
一般到特殊的方法,
类比矩形和菱形
回顾与思考:
这是研究图形的基本思路.
(1)本章研究内容:各种平行四边形的边、角、对角
线的特征;
(2)研究步骤:下定义→探性质→研判定;
(3)研究方法:观察、猜想、证明;建立当前图形
(平行四边形)与三角形的联系;从性质定理的
逆命题的讨论中研究判定定理;类比、一般到特
殊.
回顾与思考:
一、几种特殊四边形的性质
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
知识梳理:
四边形 条件
平行 四边形
矩形
菱形
正方形
二、几种特殊四边形的常用判定方法:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形
2.对角线互相垂直的平行四边形
3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
知识梳理:
矩形
菱形
正方形
平行四边形
四边形
知识梳理:
三、平行四边形、矩形、菱形、正方形之间的关系
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
三、平行四边形、矩形、菱形、正方形之间的关系
知识梳理:
1.两条平行线之间的距离:
2.三角形的中位线定理:
两条平行线中,一条直线上任意一点到另一条直线的距
离叫做两条平行线之间的距离.
三角形的中位线平行于第三边,并且等于第三边的一半
3.直角三角形斜边上的中线:
直角三角形斜边上的中线等于斜边的一半.
四、其他重要概念
知识梳理:
考题分类:
[考点一]:平行四边形的性质与判定
例1 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
(1)求证:四边形DEGF是平行四边形;
(2)如果点G是BC的中点,且BC=12,CD=10,求四边形AGCD的面积.
(1)证明:∵ AG∥CD,AD∥BC
∴ 四边形AGCD是平行四边形 ∴ AG=CD
∵ E、F分别为AG、CD的中点∴ EG=AG,DF=CD
∴ EG=DF且EG∥DF∴ 四边形DEGF是平行四边形
(2)解:∵ 点G是BC的中点,BC=12∴ BG=CG=BC=6
∵ 四边形AGCD是平行四边形∴ AG=CD=10
在Rt△ABG中,根据勾股定理AB===8∴ S四边形AGCD=6×8=48
考题分类:
[考点一]:平行四边形的性质与判定
例2 如图,在□ABCD中,点E在边BC上,点F在边DA的延长线上,且AF=CE,EF与AB交于点G.
(1)求证:AC∥EF;
(2)若点G是AB的中点,BE=6,求边AD的长.
(1)证明:∵ 四边形ABCD是平行四边形
∴ AD∥BC ∴ AF∥CE
又∵ AF=CE
∴ 四边形AFEC是平行四边形∴ AC∥EF
(2)解:∵ AD∥BC,∴ ∠F=∠BEG,∠FAG=∠B
∵ 点G是AB的中点,∴ AG=BG
∴ △AGF≌△BGE (AAS)∴ AF=BE=6
∴ CE=AF=6 ∴ BC=BE+CE=12
∵ 四边形ABCD是平行四边形∴ AD=BC=12
考题分类:
[考点二]:三角形的中位线与Rt△斜边上的中线
例3 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
证明:(1)∵ 点D,E,F分别是AB,BC,CA的中点
∴ DE、EF都是△ABC的中位线∴ DE∥AC,EF∥AB
∴ 四边形ADEF是平行四边形
(2)∵ 四边形ADEF是平行四边形
∴ ∠DEF=∠BAC
∵ D,F分别是AB,CA的中点,AH是边BC上的高
∴ DH、FH分别是Rt△ABH和Rt△ACH斜边上的中线
∴ DH=AD,FH=AF∴ ∠DAH=∠DHA,∠FAH=∠FHA
∵ ∠DAH+∠FAH=∠BAC ;∠DHA+∠FHA=∠DHF
∴ ∠DHF=∠BAC∴ ∠DHF=∠DEF
考题分类:
[考点三]:特殊平行四边形的性质与判定
例4 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作DE∥AC,两线相交于点E.
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥DE于点E,求∠AOD的度数.
(1)证明:∵ AE∥BD,DE∥AC∴ 四边形AODE是平行四边形
∵ 四边形ABCD是矩形∴ AC=BD,OA=AC,OD=BD
∴ OA=OD∴ 四边形AODE是菱形
(2)解:连接OE.
由(1)得,四边形AODE是菱形,∴ AE=AO=BO
∵ AE∥BO,∴ 四边形AEOB是平行四边形
∵ BE⊥DE,DE∥AC,∴ BE⊥AO
∴ 四边形AEOB是菱形∴ AE=AB=BO
∴ AB=BO=AO∴ △AOB是等边三角形
∴ ∠AOB=60°∴ ∠AOD=180°-60°=120°
考题分类:
[考点三]:特殊平行四边形的性质与判定
例5 如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.理由如下:
∵ EF垂直平分BC,∴ BF=CF,BE=CE
∴ ∠3=∠1
∵ ∠ACB=90°,∴ ∠3+∠A=90°,∠1+∠2=90°
∴ ∠2=∠A,∴ CE=AE
∴ BE=AE
∵ CF=AE
∴ BE=CE=CF=BF
∴ 四边形BECF是菱形
考题分类:
[考点三]:特殊平行四边形的性质与判定
例5 如图,已知在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(2)当∠A=45°时,四边形BECF是正方形.
证明:∵ ∠A=45°,∠ACB=90°
∴ ∠CBA=45°
∵ 四边形BECF是菱形
∴ ∠EBF=2∠CBA=90°
∴ 菱形BECF是正方形
方法总结
正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个菱形有一个角为直角;
③还可以先判定四边形是平行四边形,再用①或②进行判定.
例6 在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少.
解:如图,∵在平行四边形ABCD中,AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE.
又∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE.
(1)当AE=2时,则平行四边形的周长=2×(2+5)=14.
(2)当AE=3时,则平行四边形的周长=2×(3+5)=16.
本章思想方法:
一、分类讨论思想
例7 如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:
(1)FC的长;
(2)EF的长.
解:(1)由题意得AF=AD=10cm,
在Rt△ABF中,∵AB=8,
∴BF=6cm,
∴FC=BC-BF=10-6=4(cm).
(2)由题意可得EF=DE,可设DE的长为x,
在Rt△EFC中,(8-x)2+42=x2,
解得x=5,
即EF的长为5cm.
本章思想方法:
二、方程思想
例8 如图,平行四边形ABCD中,AC、BD为对角线,其交点为O,若BC=6,BC边上的高为4,试求阴影部分的面积.
解:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵AB∥CD,
∴∠EAO=∠HCO.
又∵ ∠AOE=∠COH,
∴△AEO≌△CHO(ASA),
同理可得△OAQ≌△OCG,△OPD≌△OFB,
∴S阴影=S△BCD= S平行四边形ABCD= ×6×4=12.
Q
G
E
H
F
P
本章思想方法:
三、转化思想
四边形
两组对边
分别平行
平行四边形
矩形
菱形
正方形
一个角是直角
一组邻
边相等
一组邻边相等
一个角
是直角
课堂小结:
课后作业:
必做题:教科书第67页复习题18第1,2,4,6,7,9,12题;
选做题:教科书第69页复习题18第14题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
