18_2_2 第2课时 菱形的判定 课件(共22张PPT)
文档属性
| 名称 | 18_2_2 第2课时 菱形的判定 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 18:29:07 | ||
图片预览




文档简介
(共22张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2特殊的平行四边形
第2课时 菱形的判定
18.2.2菱形
经历菱形的判定方法的探究过程,掌握菱形的三种判定方法.
核心素养目标:
经历利用菱形的定义探究菱形其它判定方法的过程,培养学生动手实验、观察、推理的意识,发展学生的逻辑思维能力和演绎能力;
在探究菱形判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
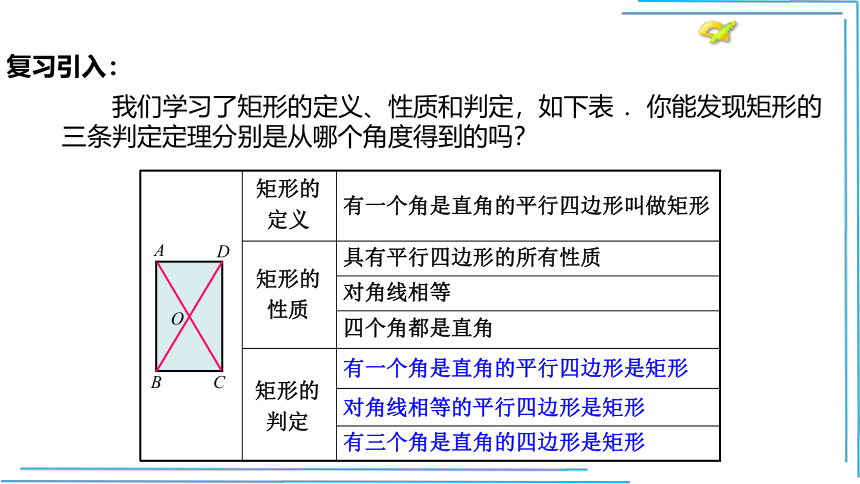
我们学习了矩形的定义、性质和判定,如下表 .你能发现矩形的三条判定定理分别是从哪个角度得到的吗?
矩形的
定义
有一个角是直角的平行四边形叫做矩形
矩形的
性质
具有平行四边形的所有性质
对角线相等
四个角都是直角
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
C
D
A
B
O
矩形的
判定
复习引入:
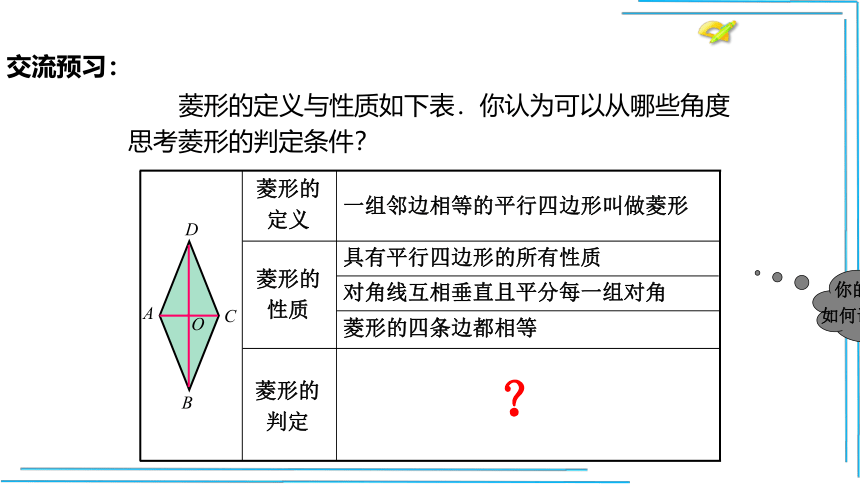
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
?
你的想法正确吗?
如何证明你的猜想?
交流预习:
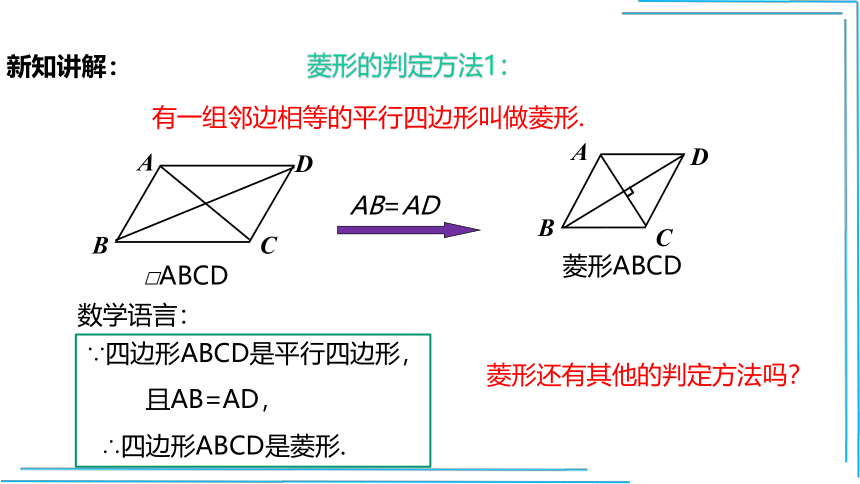
菱形的判定方法1:
有一组邻边相等的平行四边形叫做菱形.
数学语言:
∵四边形ABCD是平行四边形,
且AB=AD,
∴四边形ABCD是菱形.
菱形还有其他的判定方法吗?
新知讲解:
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
AB=AD
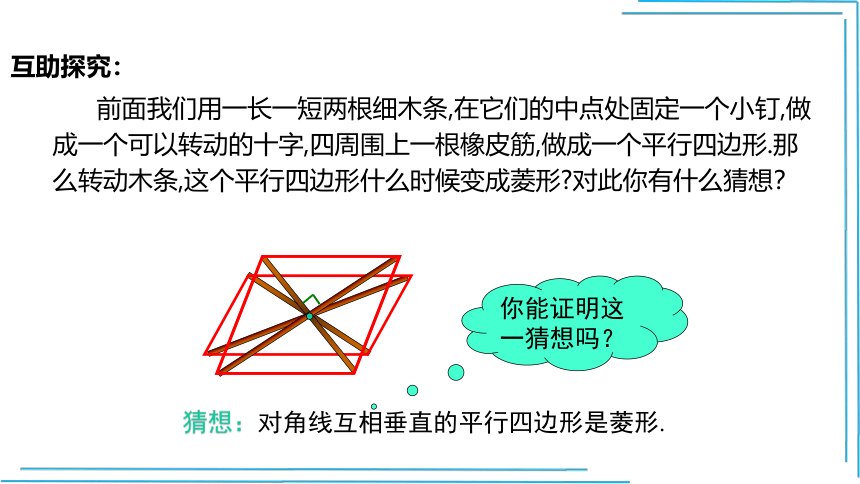
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想?
猜想:对角线互相垂直的平行四边形是菱形.
你能证明这一猜想吗?
互助探究:
A
B
C
O
D
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O,AC⊥BD.
求证:□ABCD是菱形.
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
验证猜想:
菱形的判定方法2:
对角线互相垂直的平行四边形是菱形.
数学语言:
∵在□ABCD中,AC⊥BD,
∴四边形ABCD是菱形.
新知讲解:
A
B
C
D
□ABCD
AC⊥BD
A
B
C
D
菱形ABCD
例1 如图, ABCD的两条对角线AC、BD相交于点O,AB=5, AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
又∵四边形ABCD是平行四边形,
∵ OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴四边形ABCD是菱形.
例题讲解:
分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
C
A
B
D
想一想:根据作法你有什么猜想?你能验证上面的作法吗?
猜想:四条边相等的四边形是菱形.
互助探究:
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
验证猜想:
菱形的判定方法3:
四条边都相等的四边形是菱形
数学语言:
∴四边形ABCD是菱形.
新知讲解:
AB=BC=CD=AD
四边形ABCD
A
B
C
D
A
B
C
D
菱形ABCD
∵在四边形ABCD中,AB=BC=CD=AD,
跟踪练习:
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和,这是一个特殊的平行四边形吗?为什么?求出它的面积.
解:四边形ABCD是菱形.理由如下:
∵ 四边形ABCD是平形四边形,AB=9,AC=12,BD=
∴ AO=AC=6,BO=BD=
∵ +=
即 +=
∴ AC⊥BD
∴ 四边形ABCD是菱形
∴ S菱形ABCD=×12×=
跟踪练习:
3.如图,两张等宽的纸条交叉叠放在一起,重合的四边形ABCD是一个菱形吗?为什么?
解:四边形ABCD是菱形.理由如下:
∵ AB∥CD,AD∥BC
∴ 四边形ABCD是平行四边形过点A分别作BC,CD边上
的高AE,AF,则AE=AF.
∵ S□ABCD=BC×AE=CD×AF
∴ BC=CD
∴ 四边形ABCD是菱形
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
课堂小结:
1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.
√
╳
╳
╳
2.一边长为5cm的平行四边形的两条对角线的长分别
为24cm和26cm,则平行四边形的面积是 .
312cm2
课堂检测:
A
B
C
D
O
E
3.如图,矩形ABCD的对角线相交于点O,DE∥AC,
CE ∥BD.求证:四边形OCED是菱形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形.
课堂检测:
课后作业:
必做题:教科书第58页练习第1,2,3题;
选做题:教科书第61页18.2第6,10题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2特殊的平行四边形
第2课时 菱形的判定
18.2.2菱形
经历菱形的判定方法的探究过程,掌握菱形的三种判定方法.
核心素养目标:
经历利用菱形的定义探究菱形其它判定方法的过程,培养学生动手实验、观察、推理的意识,发展学生的逻辑思维能力和演绎能力;
在探究菱形判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
我们学习了矩形的定义、性质和判定,如下表 .你能发现矩形的三条判定定理分别是从哪个角度得到的吗?
矩形的
定义
有一个角是直角的平行四边形叫做矩形
矩形的
性质
具有平行四边形的所有性质
对角线相等
四个角都是直角
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
C
D
A
B
O
矩形的
判定
复习引入:
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
?
你的想法正确吗?
如何证明你的猜想?
交流预习:
菱形的判定方法1:
有一组邻边相等的平行四边形叫做菱形.
数学语言:
∵四边形ABCD是平行四边形,
且AB=AD,
∴四边形ABCD是菱形.
菱形还有其他的判定方法吗?
新知讲解:
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
AB=AD
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想?
猜想:对角线互相垂直的平行四边形是菱形.
你能证明这一猜想吗?
互助探究:
A
B
C
O
D
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O,AC⊥BD.
求证:□ABCD是菱形.
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
验证猜想:
菱形的判定方法2:
对角线互相垂直的平行四边形是菱形.
数学语言:
∵在□ABCD中,AC⊥BD,
∴四边形ABCD是菱形.
新知讲解:
A
B
C
D
□ABCD
AC⊥BD
A
B
C
D
菱形ABCD
例1 如图, ABCD的两条对角线AC、BD相交于点O,AB=5, AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
又∵四边形ABCD是平行四边形,
∵ OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴四边形ABCD是菱形.
例题讲解:
分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
C
A
B
D
想一想:根据作法你有什么猜想?你能验证上面的作法吗?
猜想:四条边相等的四边形是菱形.
互助探究:
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
验证猜想:
菱形的判定方法3:
四条边都相等的四边形是菱形
数学语言:
∴四边形ABCD是菱形.
新知讲解:
AB=BC=CD=AD
四边形ABCD
A
B
C
D
A
B
C
D
菱形ABCD
∵在四边形ABCD中,AB=BC=CD=AD,
跟踪练习:
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和,这是一个特殊的平行四边形吗?为什么?求出它的面积.
解:四边形ABCD是菱形.理由如下:
∵ 四边形ABCD是平形四边形,AB=9,AC=12,BD=
∴ AO=AC=6,BO=BD=
∵ +=
即 +=
∴ AC⊥BD
∴ 四边形ABCD是菱形
∴ S菱形ABCD=×12×=
跟踪练习:
3.如图,两张等宽的纸条交叉叠放在一起,重合的四边形ABCD是一个菱形吗?为什么?
解:四边形ABCD是菱形.理由如下:
∵ AB∥CD,AD∥BC
∴ 四边形ABCD是平行四边形过点A分别作BC,CD边上
的高AE,AF,则AE=AF.
∵ S□ABCD=BC×AE=CD×AF
∴ BC=CD
∴ 四边形ABCD是菱形
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
课堂小结:
1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.
√
╳
╳
╳
2.一边长为5cm的平行四边形的两条对角线的长分别
为24cm和26cm,则平行四边形的面积是 .
312cm2
课堂检测:
A
B
C
D
O
E
3.如图,矩形ABCD的对角线相交于点O,DE∥AC,
CE ∥BD.求证:四边形OCED是菱形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形.
课堂检测:
课后作业:
必做题:教科书第58页练习第1,2,3题;
选做题:教科书第61页18.2第6,10题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
