18_2_1 第2课时 矩形的判定 课件(共22张PPT)
文档属性
| 名称 | 18_2_1 第2课时 矩形的判定 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 18:27:54 | ||
图片预览





文档简介
(共22张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2特殊的平行四边形
第2课时 矩形的判定
18.2.1矩形
理解并掌握矩形的判定方法;使学生能应用矩形的定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力;
核心素养目标:
让学生经历探索矩形判定定理的过程理解并掌握矩形的判定方法积累几何学习的经验,发展合情推理和演绎推理的能力;
在课堂活动中,通过观察、思考、猜想、证明,培养学生主动参与、乐于探究、勤于动手的学习习惯
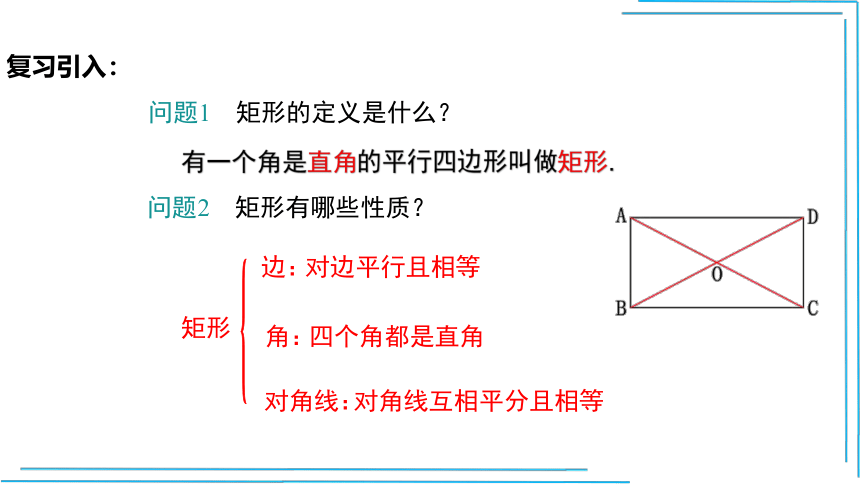
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
复习引入:
交流预习:
工人师傅做铝合金窗框,分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD,EF=GH; (2)摆放成如图②所示的四边形,则这时窗框的形状是___________,根据的数学道理是______________________________________;
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图④,说明窗框合格,这时窗框是_____,根据的数学道理是____________
平行四边形
两组对边分别相等的四边形是平行四边形
矩形
有一个角是直角的平行四边形叫做矩形
互助探究:
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形. 你知道其中的道理吗?
思考 我们知道,矩形的对角线相等.反过来,对角线相等的平行四边 形是矩形吗?
猜想:对角线相等的平行四边形是矩形.
互助探究:
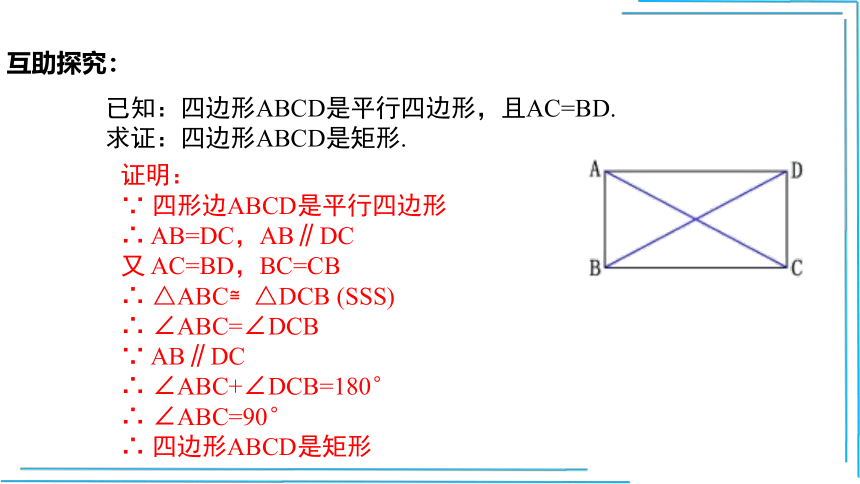
已知:四边形ABCD是平行四边形,且AC=BD.求证:四边形ABCD是矩形.
证明:
∵ 四形边ABCD是平行四边形
∴ AB=DC,AB∥DC
又 AC=BD,BC=CB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
∵ AB∥DC
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=90°
∴ 四边形ABCD是矩形
对角线相等的平行四边形是矩形.
几何语言描述:
在平行四边形ABCD中,
∵AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
新知讲解:
矩形的判定定理1
问题:对角线互相平分且相等的四边形是矩形吗?为什么?
问题1 上节课我们研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
互助探究:
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
A
B
C
D
互助探究:
有三个角是直角的四边形是矩形.
几何语言描述:
在四边形ABCD中,∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
A
B
C
D
新知讲解:
矩形的判定定理2
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
例2 如图,在□ABCD中,对角线AC,BD相 交于点O,且OA=OD,∠OAD=50°. 求∠OAB的度数.
例题精讲:
跟踪练习:
1.八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线.如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
解:由于矩形对角线互相平分且相等,所以如果一条对角线用了38盆红花,那么还需要从花房运来38盆红花;如果一条对角线用了49盆红花,那么在对角线的交点处一盆,两边各24盆,所以还需要从花房运来48盆红花.
跟踪练习:
2.如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,求□ABCD的面积.
解:∵ 四边形ABCD是平行四边形
∴ AC=2AO,BD=2BO
∵ △OAB是等边三角形
∴ AO=BO=AB=4
∴ AC=BD=8
∴ 四边形ABCD是矩形
∴ ∠ABC=90°
∴ 在Rt△ABC中,BC===4
∴ S□ABCD=AB×BC=4×4=
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
课堂小结:
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(4)有三个角都相等的四边形是矩形;
×
×
×
×
√
√
√
√
(8)一组对角互补的平行四边形是矩形;
课堂检测:
2.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、 ∠MCA、 ∠ ACN、∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定
D
E
F
M
N
Q
P
A
B
C
C
课堂检测:
3.如图 ABCD中, ∠1= ∠2中.此时四边形ABCD是矩形吗?为什么?
A
B
C
D
O
1
2
解:四边形ABCD是矩形.理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
又∵ ∠1= ∠2
∴AO=BO
∴AC=BD
∴四边形ABCD是矩形.
课堂检测:
课后作业:
必做题:60页习题18.2第1、2题
选做题:60页习题18.2第3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2特殊的平行四边形
第2课时 矩形的判定
18.2.1矩形
理解并掌握矩形的判定方法;使学生能应用矩形的定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力;
核心素养目标:
让学生经历探索矩形判定定理的过程理解并掌握矩形的判定方法积累几何学习的经验,发展合情推理和演绎推理的能力;
在课堂活动中,通过观察、思考、猜想、证明,培养学生主动参与、乐于探究、勤于动手的学习习惯
问题1 矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2 矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
复习引入:
交流预习:
工人师傅做铝合金窗框,分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD,EF=GH; (2)摆放成如图②所示的四边形,则这时窗框的形状是___________,根据的数学道理是______________________________________;
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图④,说明窗框合格,这时窗框是_____,根据的数学道理是____________
平行四边形
两组对边分别相等的四边形是平行四边形
矩形
有一个角是直角的平行四边形叫做矩形
互助探究:
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形. 你知道其中的道理吗?
思考 我们知道,矩形的对角线相等.反过来,对角线相等的平行四边 形是矩形吗?
猜想:对角线相等的平行四边形是矩形.
互助探究:
已知:四边形ABCD是平行四边形,且AC=BD.求证:四边形ABCD是矩形.
证明:
∵ 四形边ABCD是平行四边形
∴ AB=DC,AB∥DC
又 AC=BD,BC=CB
∴ △ABC≌△DCB (SSS)
∴ ∠ABC=∠DCB
∵ AB∥DC
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=90°
∴ 四边形ABCD是矩形
对角线相等的平行四边形是矩形.
几何语言描述:
在平行四边形ABCD中,
∵AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
新知讲解:
矩形的判定定理1
问题:对角线互相平分且相等的四边形是矩形吗?为什么?
问题1 上节课我们研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
互助探究:
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
A
B
C
D
互助探究:
有三个角是直角的四边形是矩形.
几何语言描述:
在四边形ABCD中,∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
A
B
C
D
新知讲解:
矩形的判定定理2
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
例2 如图,在□ABCD中,对角线AC,BD相 交于点O,且OA=OD,∠OAD=50°. 求∠OAB的度数.
例题精讲:
跟踪练习:
1.八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线.如果一条对角线用了38盆红花,还需要从花房运来多少盆红花?为什么?如果一条对角线用了49盆呢?
解:由于矩形对角线互相平分且相等,所以如果一条对角线用了38盆红花,那么还需要从花房运来38盆红花;如果一条对角线用了49盆红花,那么在对角线的交点处一盆,两边各24盆,所以还需要从花房运来48盆红花.
跟踪练习:
2.如图,□ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,求□ABCD的面积.
解:∵ 四边形ABCD是平行四边形
∴ AC=2AO,BD=2BO
∵ △OAB是等边三角形
∴ AO=BO=AB=4
∴ AC=BD=8
∴ 四边形ABCD是矩形
∴ ∠ABC=90°
∴ 在Rt△ABC中,BC===4
∴ S□ABCD=AB×BC=4×4=
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
课堂小结:
1.下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(4)有三个角都相等的四边形是矩形;
×
×
×
×
√
√
√
√
(8)一组对角互补的平行四边形是矩形;
课堂检测:
2.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、 ∠MCA、 ∠ ACN、∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定
D
E
F
M
N
Q
P
A
B
C
C
课堂检测:
3.如图 ABCD中, ∠1= ∠2中.此时四边形ABCD是矩形吗?为什么?
A
B
C
D
O
1
2
解:四边形ABCD是矩形.理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
又∵ ∠1= ∠2
∴AO=BO
∴AC=BD
∴四边形ABCD是矩形.
课堂检测:
课后作业:
必做题:60页习题18.2第1、2题
选做题:60页习题18.2第3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
