18_2_1 第1课时 矩形的性质 课件(共23张PPT)
文档属性
| 名称 | 18_2_1 第1课时 矩形的性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 18:38:43 | ||
图片预览






文档简介
(共23张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2 特殊的平行四边形
第1课时 矩形的性质
18.2.1矩形
理解矩形的概念,了解它与平行四边形之间的关系;
核心素养目标:
经历矩形性质定理和判定定理的探索过程,发展学生的合情推理能力;
探索并掌握直角三角形的性质定理.
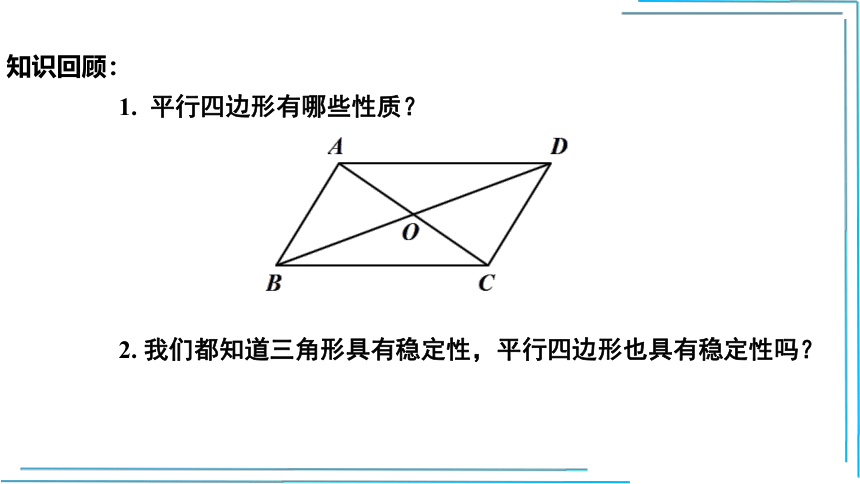
1. 平行四边形有哪些性质?
2. 我们都知道三角形具有稳定性,平行四边形也具有稳定性吗?
知识回顾:
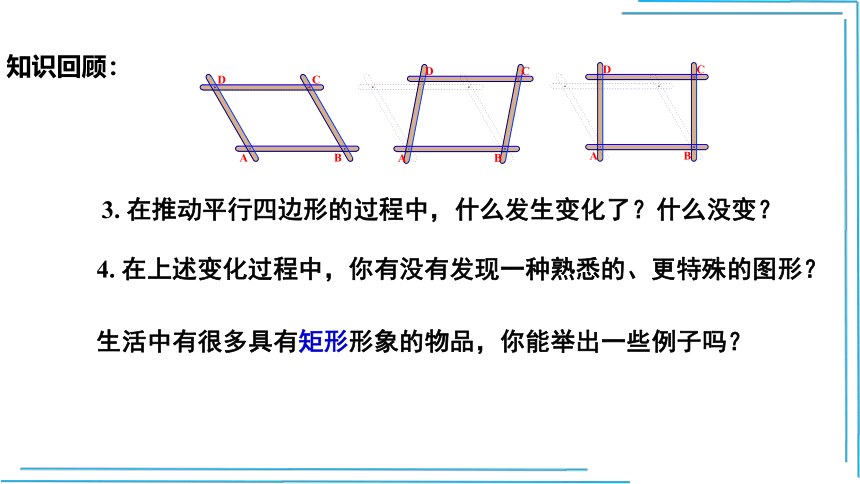
3. 在推动平行四边形的过程中,什么发生变化了?什么没变?
4. 在上述变化过程中,你有没有发现一种熟悉的、更特殊的图形?
生活中有很多具有矩形形象的物品,你能举出一些例子吗?
知识回顾:
观察下面图形,长方形在生活中无处不在.
情境引入:
活动:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
定义:有一个角是直角的平行四边形叫做矩形.
矩形
思考:矩形与平行四边形有什么关系呢?
互助探究:
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
互助探究:
在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上,拉动一对不相邻的顶点,改变平行四边形的形状。
B
互助探究:
(1)随着∠a的变化,两条对角线的长度怎样变化的?
(2)当∠a变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?
(3)当∠a是直角时,平行四边形变成矩形,此时
两条对角线的长度有什么关系?
随着∠a的变化,一条对角线在变长,一条在变短。
都变为了直角
两条对角线相等
互助探究:
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,求证:∠A=∠B=∠C=∠D=90°.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明:
∵ 四边形ABCD是矩形,
∴∠A=90°,四边形ABCD是平行四边形.
∴∠C=∠A=90°,
∠B=180°-∠A=90°,
∠D=180°-∠A=90°.
∴四边形ABCD是矩形.
D
B
C
A
矩形的性质1
生成新知:
定理:矩形的两条对角线相等.
已知:AC,BD是矩形ABCD的两条对角线.求证: AC=BD.
证明:
∵ 四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=900.
分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.
D
B
C
A
∵BC=CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
矩形的性质2
生成新知:
A
B
C
D
O
活动:如图,一张矩形纸片,沿着对角线剪去一半,你能
得到什么结论?
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?
它的长度与斜边AC有什么关系?
1
2
1
2
BO= BD= AC
猜想:直角三角形斜边上的中线等于斜边的一半.
试给出数学证明.
互助探究:
O
C
B
A
D
证明: 延长BO至D, 使OD=BO,
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴平行四边形ABCD是矩形
∴AC=BD
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO = AC
∴BO= BD= AC
互助探究:
例题精讲:
跟踪练习:
跟踪练习:
矩形的相关概念及性质
具有平行四边行的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
课堂小结:
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是( )
A.20 ° B.40° C.80 ° D.10°
A
C
C
课堂检测:
课后作业:
必做题:60页习题18.2第1、2题;
选做题:60页习题18.2第3、4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2 特殊的平行四边形
第1课时 矩形的性质
18.2.1矩形
理解矩形的概念,了解它与平行四边形之间的关系;
核心素养目标:
经历矩形性质定理和判定定理的探索过程,发展学生的合情推理能力;
探索并掌握直角三角形的性质定理.
1. 平行四边形有哪些性质?
2. 我们都知道三角形具有稳定性,平行四边形也具有稳定性吗?
知识回顾:
3. 在推动平行四边形的过程中,什么发生变化了?什么没变?
4. 在上述变化过程中,你有没有发现一种熟悉的、更特殊的图形?
生活中有很多具有矩形形象的物品,你能举出一些例子吗?
知识回顾:
观察下面图形,长方形在生活中无处不在.
情境引入:
活动:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
定义:有一个角是直角的平行四边形叫做矩形.
矩形
思考:矩形与平行四边形有什么关系呢?
互助探究:
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
互助探究:
在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上,拉动一对不相邻的顶点,改变平行四边形的形状。
B
互助探究:
(1)随着∠a的变化,两条对角线的长度怎样变化的?
(2)当∠a变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?
(3)当∠a是直角时,平行四边形变成矩形,此时
两条对角线的长度有什么关系?
随着∠a的变化,一条对角线在变长,一条在变短。
都变为了直角
两条对角线相等
互助探究:
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,求证:∠A=∠B=∠C=∠D=90°.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明:
∵ 四边形ABCD是矩形,
∴∠A=90°,四边形ABCD是平行四边形.
∴∠C=∠A=90°,
∠B=180°-∠A=90°,
∠D=180°-∠A=90°.
∴四边形ABCD是矩形.
D
B
C
A
矩形的性质1
生成新知:
定理:矩形的两条对角线相等.
已知:AC,BD是矩形ABCD的两条对角线.求证: AC=BD.
证明:
∵ 四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=900.
分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.
D
B
C
A
∵BC=CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
矩形的性质2
生成新知:
A
B
C
D
O
活动:如图,一张矩形纸片,沿着对角线剪去一半,你能
得到什么结论?
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?
它的长度与斜边AC有什么关系?
1
2
1
2
BO= BD= AC
猜想:直角三角形斜边上的中线等于斜边的一半.
试给出数学证明.
互助探究:
O
C
B
A
D
证明: 延长BO至D, 使OD=BO,
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴平行四边形ABCD是矩形
∴AC=BD
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证: BO = AC
∴BO= BD= AC
互助探究:
例题精讲:
跟踪练习:
跟踪练习:
矩形的相关概念及性质
具有平行四边行的一切性质
四个内角都是直角,
两条对角线互相平分且相等
轴对称图形
有两条对称轴
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形
课堂小结:
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是( )
A.20 ° B.40° C.80 ° D.10°
A
C
C
课堂检测:
课后作业:
必做题:60页习题18.2第1、2题;
选做题:60页习题18.2第3、4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
