18_2_2 第1课时 菱形的性质 课件(共24张PPT)
文档属性
| 名称 | 18_2_2 第1课时 菱形的性质 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 18:52:50 | ||
图片预览





文档简介
(共24张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2特殊的平行四边形
第1课时 菱形的性质
18.2.2菱形
理解菱形的定义,掌握菱形的特殊性质;理解菱形的面积公式,会选择适当的方法计算菱形的面积;
核心素养目标:
通过观察、实验、猜想、验证、推理交流等数学活动,发展学生的合情推理能力和动手操作能力及应用数学的意识与能力;
在应用菱形性质的过程中培养学生独立思考的习惯,在数学学习活动中获得成功的体验,通过菱形性质的探索学习,体会它的内在美和应用美.
平行
四边形
矩形
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
有一个角是直角
复习引入:
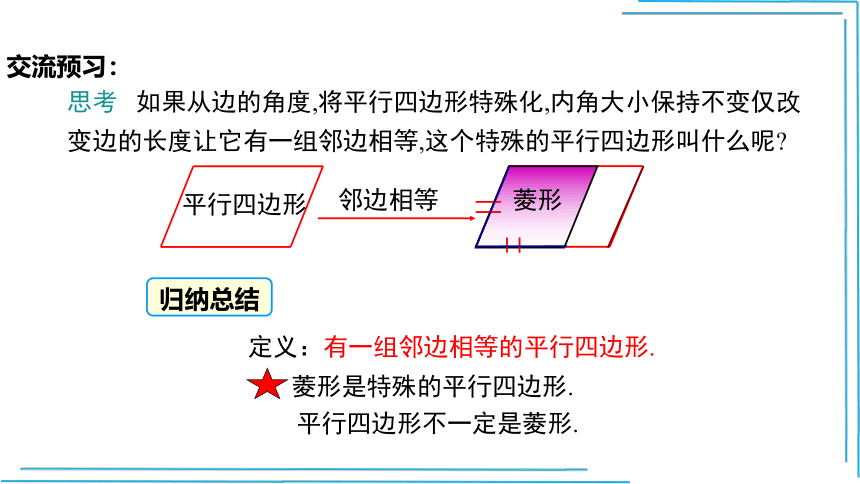
思考 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
定义:有一组邻边相等的平行四边形.
菱形
邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
归纳总结
交流预习:
提出猜想:
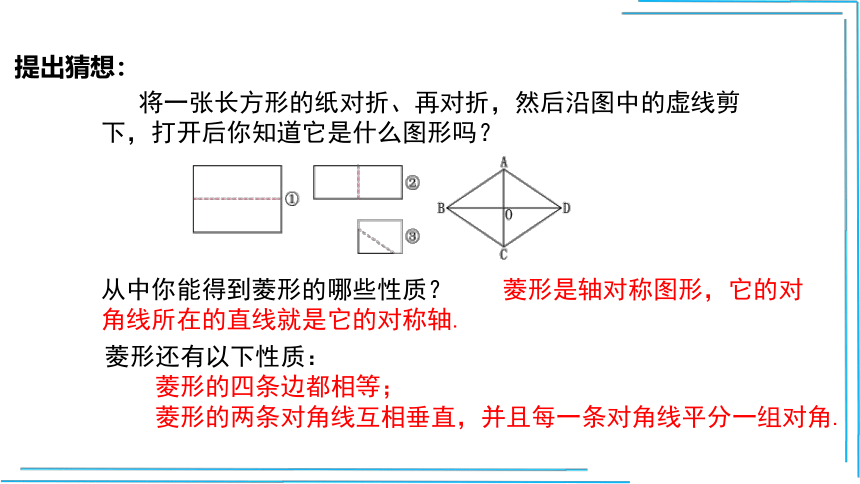
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开后你知道它是什么图形吗?
从中你能得到菱形的哪些性质? 菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.
菱形还有以下性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
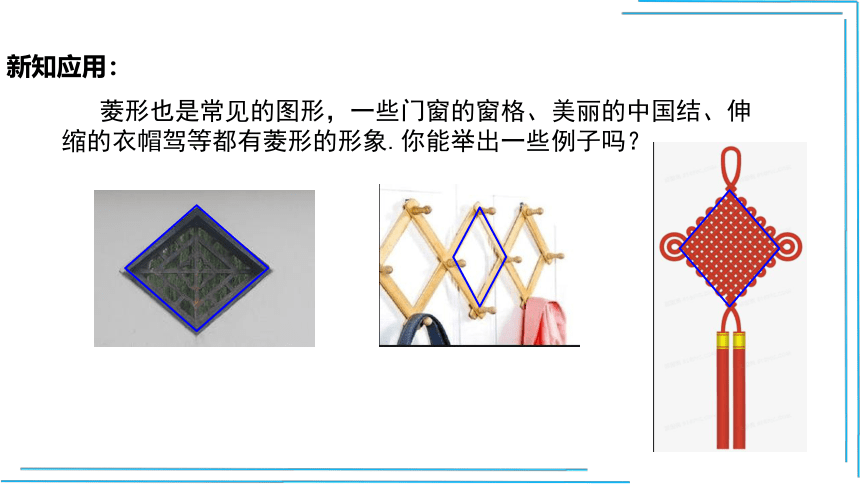
菱形也是常见的图形,一些门窗的窗格、美丽的中国结、伸缩的衣帽驾等都有菱形的形象.你能举出一些例子吗?
新知应用:
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
(3)∠DAC=∠BAC,∠DCA=∠BCA,∠ADB=∠CDB,∠ABD=∠CBD.
证明:(1)∵四边形ABCD是菱形,
∴AB = CD,AD = BC(菱形的对边相等).
又∵AB=AD;
∴AB = BC = CD =AD.
A
B
C
O
D
验证猜想:
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD . (菱形的对角线互相平分)
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
A
B
C
O
D
互助探究:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
B
D
A
C
符号语言:
∵四边形ABCD是菱形,
∴ AC⊥BD ;
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC.
生成新知:
互助探究:
如图,比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成四个全等的三角形,而平行四边形通常只被分成两对全等的三角形.
A
B
D
C
a
h
(1)S = a·h.
(2)S = S△ABD+S△BCD
= AO·DB + CO·DB = AC·DB.
O
菱形的面积计算公式:
菱形的面积 = 底×高 = 对角线乘积的一半
新知讲解:
例题讲解:
例3 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
B
A
O
C
D
解:∵花坛ABCD是菱形,
例题讲解:
跟踪练习:
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
解:∵ 四边形ABCD是菱形
∴ AC⊥BD,BD=2OB,AC=2AO=8
在Rt△AOB中,OB===3
∴ BD=6
跟踪练习:
2.已知菱形的两对角线的长分别是6和8,求菱形的周长和面积.
解:∵ 四边形ABCD是菱形,且AC=8,BD=6
∴ AC⊥BD,AO=AC=4,BO=BD=3
在Rt△AOB中,AB===5
∴ C菱形ABCD=4×5=20
S菱形ABCD=×6×8=24
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结:
1.填一填:根据右图填空
(1)已知菱形的周长是12cm,那么它的边长是______.
(2)菱形ABCD中,∠ABC=120 °,则∠BAC=_______.
(3)菱形的两条对角线长分别为6cm和8cm,则菱形的边长是_______.
3cm
30°
A
B
C
O
D
5cm
课堂检测:
(4)菱形的一个内角为120°,平分这个内角的对角线长为11cm,菱形的周长为______.
44cm
(5)菱形的面积为64平方厘米,两条对角线的比为1∶2 ,那么菱形的边长为_______.
8厘米
课堂检测:
2.已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
课堂检测:
课后作业:
必做题:教科书第60页习题18.2第5,7题;
选做题:教科书第61页习题18.2第11题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.2特殊的平行四边形
第1课时 菱形的性质
18.2.2菱形
理解菱形的定义,掌握菱形的特殊性质;理解菱形的面积公式,会选择适当的方法计算菱形的面积;
核心素养目标:
通过观察、实验、猜想、验证、推理交流等数学活动,发展学生的合情推理能力和动手操作能力及应用数学的意识与能力;
在应用菱形性质的过程中培养学生独立思考的习惯,在数学学习活动中获得成功的体验,通过菱形性质的探索学习,体会它的内在美和应用美.
平行
四边形
矩形
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
有一个角是直角
复习引入:
思考 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
定义:有一组邻边相等的平行四边形.
菱形
邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
归纳总结
交流预习:
提出猜想:
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开后你知道它是什么图形吗?
从中你能得到菱形的哪些性质? 菱形是轴对称图形,它的对角线所在的直线就是它的对称轴.
菱形还有以下性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形也是常见的图形,一些门窗的窗格、美丽的中国结、伸缩的衣帽驾等都有菱形的形象.你能举出一些例子吗?
新知应用:
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
(3)∠DAC=∠BAC,∠DCA=∠BCA,∠ADB=∠CDB,∠ABD=∠CBD.
证明:(1)∵四边形ABCD是菱形,
∴AB = CD,AD = BC(菱形的对边相等).
又∵AB=AD;
∴AB = BC = CD =AD.
A
B
C
O
D
验证猜想:
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD . (菱形的对角线互相平分)
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
A
B
C
O
D
互助探究:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
B
D
A
C
符号语言:
∵四边形ABCD是菱形,
∴ AC⊥BD ;
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC.
生成新知:
互助探究:
如图,比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成四个全等的三角形,而平行四边形通常只被分成两对全等的三角形.
A
B
D
C
a
h
(1)S = a·h.
(2)S = S△ABD+S△BCD
= AO·DB + CO·DB = AC·DB.
O
菱形的面积计算公式:
菱形的面积 = 底×高 = 对角线乘积的一半
新知讲解:
例题讲解:
例3 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
B
A
O
C
D
解:∵花坛ABCD是菱形,
例题讲解:
跟踪练习:
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
解:∵ 四边形ABCD是菱形
∴ AC⊥BD,BD=2OB,AC=2AO=8
在Rt△AOB中,OB===3
∴ BD=6
跟踪练习:
2.已知菱形的两对角线的长分别是6和8,求菱形的周长和面积.
解:∵ 四边形ABCD是菱形,且AC=8,BD=6
∴ AC⊥BD,AO=AC=4,BO=BD=3
在Rt△AOB中,AB===5
∴ C菱形ABCD=4×5=20
S菱形ABCD=×6×8=24
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结:
1.填一填:根据右图填空
(1)已知菱形的周长是12cm,那么它的边长是______.
(2)菱形ABCD中,∠ABC=120 °,则∠BAC=_______.
(3)菱形的两条对角线长分别为6cm和8cm,则菱形的边长是_______.
3cm
30°
A
B
C
O
D
5cm
课堂检测:
(4)菱形的一个内角为120°,平分这个内角的对角线长为11cm,菱形的周长为______.
44cm
(5)菱形的面积为64平方厘米,两条对角线的比为1∶2 ,那么菱形的边长为_______.
8厘米
课堂检测:
2.已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
课堂检测:
课后作业:
必做题:教科书第60页习题18.2第5,7题;
选做题:教科书第61页习题18.2第11题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
