18.2.2 第2课时 菱形的判定教案【2023春人教版八下数学优质备课】
文档属性
| 名称 | 18.2.2 第2课时 菱形的判定教案【2023春人教版八下数学优质备课】 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 08:25:58 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
教学章节 第十八章 课 型 新授课 年 月 日
课 题 18.2.2第二课时 菱形的判定
课标解读 1.理解菱形的概念; 2.探索并证明菱形的性质定理:菱形的四条边都相等;两条对角线互相垂直,并且每一条对角线平分一组对角。
核心 素养 目标 1.经历菱形的判定方法的探究过程,掌握菱形的三种判定方法; 2.经历利用菱形的定义探究菱形其它判定方法的过程,培养学生动手实验、观察、推理的意识,发展学生的逻辑思维能力和演绎能力; 3.在探究菱形判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
教学重点 菱形的判定定理的探究.
教学难点 菱形的性质与判定的综合应用.
导学过程 学法指导
【课前预习案】
知识回顾 我们学习了矩形的定义、性质和判定,如下表 .你能发现矩形的三条判定定理分别是从哪个角度得到的吗? 交流预习 菱形的定义与性质如下表.你认为可以从哪些角度思考菱形的判定条件?
【课堂探究案】
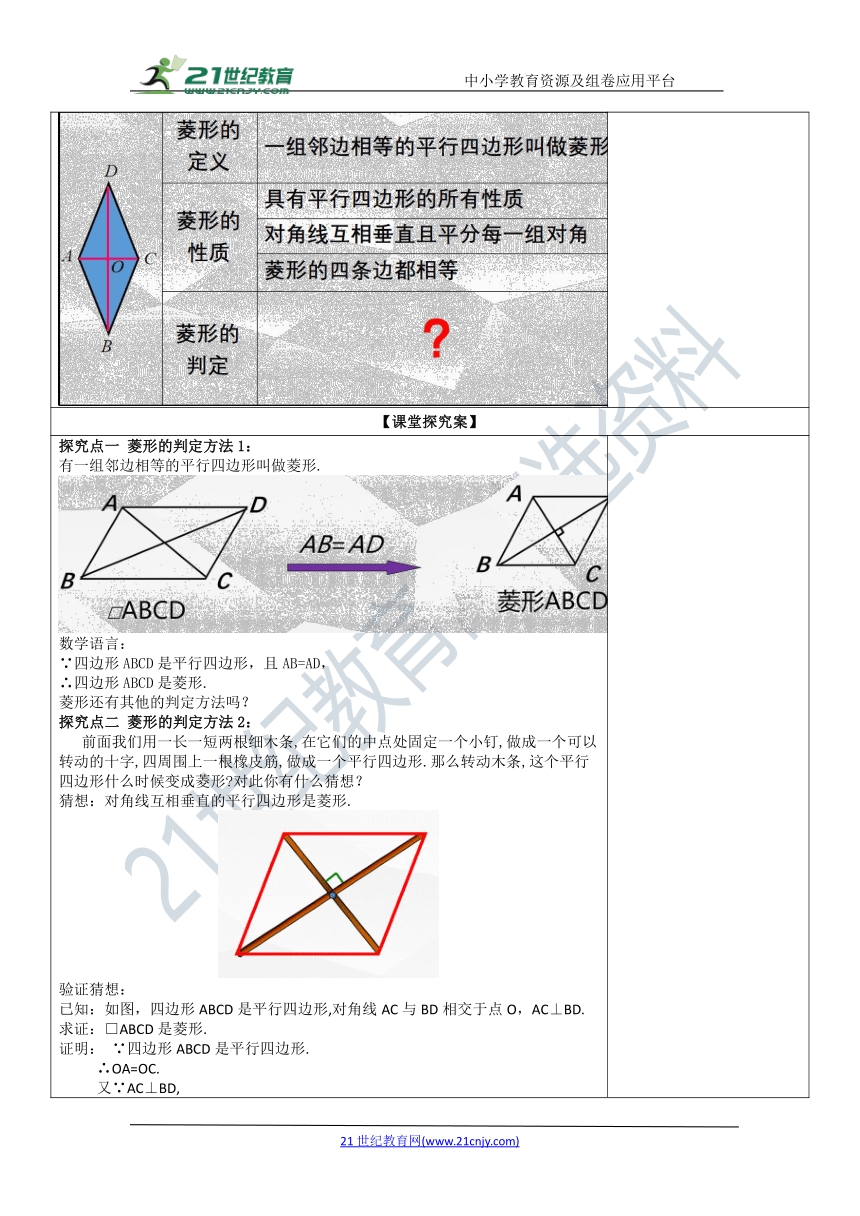
探究点一 菱形的判定方法1: 有一组邻边相等的平行四边形叫做菱形. 数学语言: ∵四边形ABCD是平行四边形,且AB=AD, ∴四边形ABCD是菱形. 菱形还有其他的判定方法吗? 探究点二 菱形的判定方法2: 前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想? 猜想:对角线互相垂直的平行四边形是菱形. 验证猜想: 已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O,AC⊥BD. 求证:□ABCD是菱形. 证明: ∵四边形ABCD是平行四边形. ∴OA=OC. 又∵AC⊥BD, ∴BD是线段AC的垂直平分线. ∴BA=BC. ∴四边形ABCD是菱形(菱形的定义). 对角线互相垂直的平行四边形是菱形. 数学语言: ∵在□ABCD中,AC⊥BD, ∴四边形ABCD是菱形. 探究点三 菱形的判定方法3: 已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗? 分别以A、C为圆心,以大于1/2 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点. 想一想:根据作法你有什么猜想?你能验证上面的作法吗? 猜想:四条边相等的四边形是菱形. 验证猜想: 已知:如图,四边形ABCD中,AB=BC=CD=AD. 求证:四边形ABCD是菱形. 证明:∵AB=BC=CD=AD; ∴AB=CD , BC=AD. ∴四边形ABCD是平行四边形. 又∵AB=BC, ∴四边形ABCD是菱形.
【课堂检测案】
例4如图,□ABCD的对角线AC、BD交于点O,且AB=5,AO=4,BO=3.求证:□ABCD是菱形. 证明:∵ AB=5,AO=4,BO=3
∴ AB2=AO2+BO2
∴ △OAB是直角三角形
∴ AC⊥BD
∴ □ABCD是菱形 四条边都相等的四边形是菱形 数学语言: ∵在四边形ABCD中,AB=BC=CD=AD, ∴四边形ABCD是菱形.
【课堂训练案】
例4如图,□ABCD的对角线AC、BD交于点O,且AB=5,AO=4,BO=3.求证:□ABCD是菱形. 证明:∵ AB=5,AO=4,BO=3
∴ AB2=AO2+BO2
∴ △OAB是直角三角形
∴ AC⊥BD
∴ □ABCD是菱形 2.一个平行四边形的一条边长是9,两条对角线的长分别是12和,这是一个特殊的平行四边形吗?为什么?求出它的面积. 解:四边形ABCD是菱形.理由如下:
∵ 四边形ABCD是平形四边形,AB=9,AC=12,BD=
∴ AO=AC=6,BO=BD=
∵ 62+()2=92
即 AO2+BO2=AB2
∴ AC⊥BD
∴ 四边形ABCD是菱形
∴ S菱形ABCD=×12×= 3.如图,两张等宽的纸条交叉叠放在一起,重合的四边形ABCD是一个菱形吗?为什么? 解:四边形ABCD是菱形.理由如下:
∵ AB∥CD,AD∥BC
∴ 四边形ABCD是平行四边形过点A分别作BC,CD边上 的高AE,AF,则AE=AF.
∵ S□ABCD=BC×AE=CD×AF
∴ BC=CD
∴ 四边形ABCD是菱形 1.判断下列说法是否正确 (1)对角线互相垂直的四边形是菱形; (2)对角线互相垂直且平分的四边形是菱形; (3)对角线互相垂直,且有一组邻边相等的四边形是菱形; (4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形. 2.一边长为5cm的平行四边形的两条对角线的长分别为24cm和26cm,则平行四边形的面积是 . 3.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.求证:四边形OCED是菱形. 证明:∵DE∥AC,CE∥BD, ∴四边形OCED是平行四边形. ∵四边形ABCD是矩形, ∴OC=OD, ∴四边形OCED是菱形.
课后作业 必做题:教科书第58页练习第1,2,3题; 选做题:教科书第61页18.2第6,10题.
板书设计
教学反思 在运用判定时,要遵循先易后难的原则,让学生先会运用判定解决简单的证明题,再由浅入深,学会灵活运用. 通过做不同形式的练习题,让学生能准确掌握菱形的判定并会灵活运用.
21世纪教育网(www.21cnjy.com)
教学章节 第十八章 课 型 新授课 年 月 日
课 题 18.2.2第二课时 菱形的判定
课标解读 1.理解菱形的概念; 2.探索并证明菱形的性质定理:菱形的四条边都相等;两条对角线互相垂直,并且每一条对角线平分一组对角。
核心 素养 目标 1.经历菱形的判定方法的探究过程,掌握菱形的三种判定方法; 2.经历利用菱形的定义探究菱形其它判定方法的过程,培养学生动手实验、观察、推理的意识,发展学生的逻辑思维能力和演绎能力; 3.在探究菱形判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
教学重点 菱形的判定定理的探究.
教学难点 菱形的性质与判定的综合应用.
导学过程 学法指导
【课前预习案】
知识回顾 我们学习了矩形的定义、性质和判定,如下表 .你能发现矩形的三条判定定理分别是从哪个角度得到的吗? 交流预习 菱形的定义与性质如下表.你认为可以从哪些角度思考菱形的判定条件?
【课堂探究案】
探究点一 菱形的判定方法1: 有一组邻边相等的平行四边形叫做菱形. 数学语言: ∵四边形ABCD是平行四边形,且AB=AD, ∴四边形ABCD是菱形. 菱形还有其他的判定方法吗? 探究点二 菱形的判定方法2: 前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想? 猜想:对角线互相垂直的平行四边形是菱形. 验证猜想: 已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O,AC⊥BD. 求证:□ABCD是菱形. 证明: ∵四边形ABCD是平行四边形. ∴OA=OC. 又∵AC⊥BD, ∴BD是线段AC的垂直平分线. ∴BA=BC. ∴四边形ABCD是菱形(菱形的定义). 对角线互相垂直的平行四边形是菱形. 数学语言: ∵在□ABCD中,AC⊥BD, ∴四边形ABCD是菱形. 探究点三 菱形的判定方法3: 已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗? 分别以A、C为圆心,以大于1/2 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点. 想一想:根据作法你有什么猜想?你能验证上面的作法吗? 猜想:四条边相等的四边形是菱形. 验证猜想: 已知:如图,四边形ABCD中,AB=BC=CD=AD. 求证:四边形ABCD是菱形. 证明:∵AB=BC=CD=AD; ∴AB=CD , BC=AD. ∴四边形ABCD是平行四边形. 又∵AB=BC, ∴四边形ABCD是菱形.
【课堂检测案】
例4如图,□ABCD的对角线AC、BD交于点O,且AB=5,AO=4,BO=3.求证:□ABCD是菱形. 证明:∵ AB=5,AO=4,BO=3
∴ AB2=AO2+BO2
∴ △OAB是直角三角形
∴ AC⊥BD
∴ □ABCD是菱形 四条边都相等的四边形是菱形 数学语言: ∵在四边形ABCD中,AB=BC=CD=AD, ∴四边形ABCD是菱形.
【课堂训练案】
例4如图,□ABCD的对角线AC、BD交于点O,且AB=5,AO=4,BO=3.求证:□ABCD是菱形. 证明:∵ AB=5,AO=4,BO=3
∴ AB2=AO2+BO2
∴ △OAB是直角三角形
∴ AC⊥BD
∴ □ABCD是菱形 2.一个平行四边形的一条边长是9,两条对角线的长分别是12和,这是一个特殊的平行四边形吗?为什么?求出它的面积. 解:四边形ABCD是菱形.理由如下:
∵ 四边形ABCD是平形四边形,AB=9,AC=12,BD=
∴ AO=AC=6,BO=BD=
∵ 62+()2=92
即 AO2+BO2=AB2
∴ AC⊥BD
∴ 四边形ABCD是菱形
∴ S菱形ABCD=×12×= 3.如图,两张等宽的纸条交叉叠放在一起,重合的四边形ABCD是一个菱形吗?为什么? 解:四边形ABCD是菱形.理由如下:
∵ AB∥CD,AD∥BC
∴ 四边形ABCD是平行四边形过点A分别作BC,CD边上 的高AE,AF,则AE=AF.
∵ S□ABCD=BC×AE=CD×AF
∴ BC=CD
∴ 四边形ABCD是菱形 1.判断下列说法是否正确 (1)对角线互相垂直的四边形是菱形; (2)对角线互相垂直且平分的四边形是菱形; (3)对角线互相垂直,且有一组邻边相等的四边形是菱形; (4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形. 2.一边长为5cm的平行四边形的两条对角线的长分别为24cm和26cm,则平行四边形的面积是 . 3.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.求证:四边形OCED是菱形. 证明:∵DE∥AC,CE∥BD, ∴四边形OCED是平行四边形. ∵四边形ABCD是矩形, ∴OC=OD, ∴四边形OCED是菱形.
课后作业 必做题:教科书第58页练习第1,2,3题; 选做题:教科书第61页18.2第6,10题.
板书设计
教学反思 在运用判定时,要遵循先易后难的原则,让学生先会运用判定解决简单的证明题,再由浅入深,学会灵活运用. 通过做不同形式的练习题,让学生能准确掌握菱形的判定并会灵活运用.
21世纪教育网(www.21cnjy.com)
