18_2.3 第2课时 正方形的判定分层作业(原卷版+解析版)【2023春人教版八下数学优质备课】
文档属性
| 名称 | 18_2.3 第2课时 正方形的判定分层作业(原卷版+解析版)【2023春人教版八下数学优质备课】 | 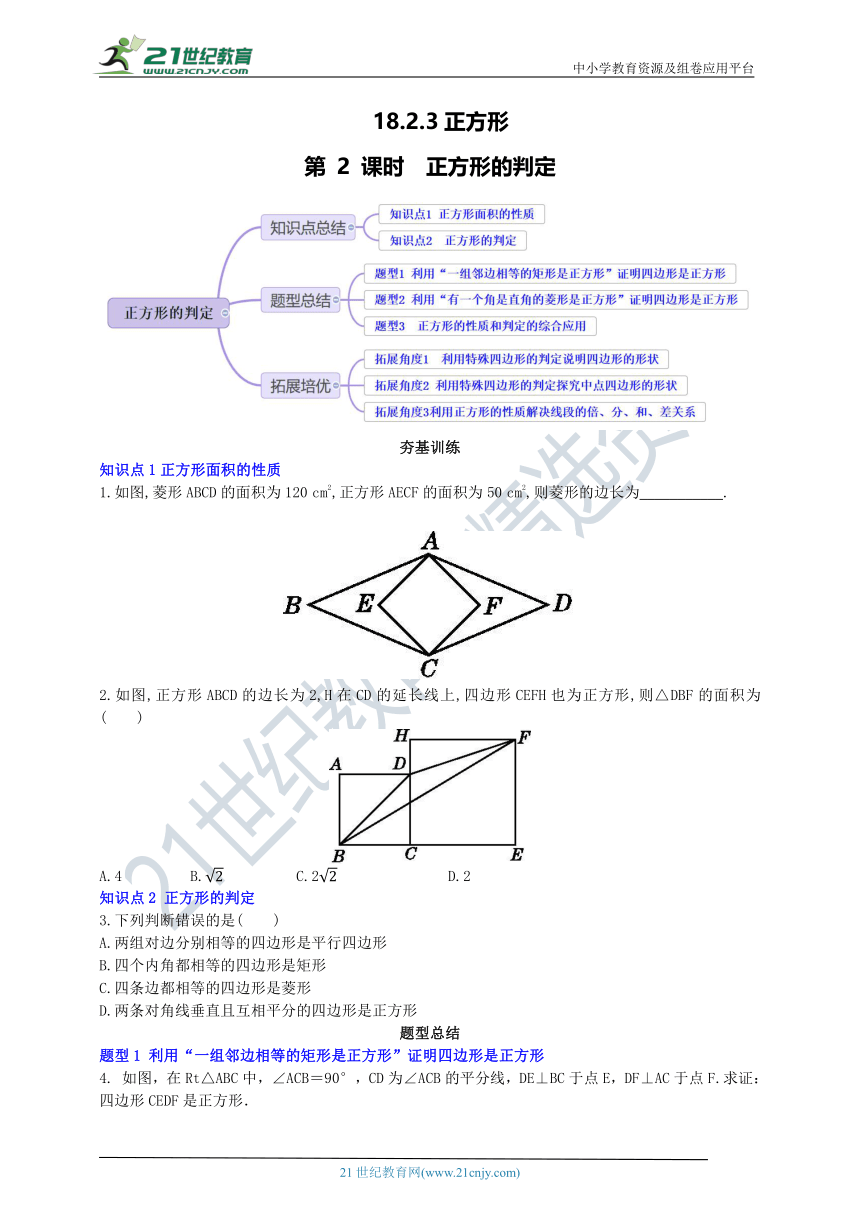 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 08:32:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
18.2.3正方形
第 2 课时 正方形的判定
夯基训练
知识点1正方形面积的性质
1.如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为___________.版权所有
2.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )1-cn-jy.com
A.4 B. C.2 D.2
知识点2 正方形的判定
3.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
题型总结
题型1 利用“一组邻边相等的矩形是正方形”证明四边形是正方形
如图,在Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
5.如图所示,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.21
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
题型2 利用“有一个角是直角的菱形是正方形”证明四边形是正方形
6.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
7.如图所示, ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=____________时,四边形ACED是正方形.请说明理由. 21·世纪*教育网
题型3 正方形的性质和判定的综合应用
8. 如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.求证:
(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
9.如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平
分线于点E,交∠BCA的外角∠ACG的平分线于点F,连接AE、AF.
(1)求证:∠ECF=90°;
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
(3)在(2)的条件下,要使四边形AECF为正方形,△ABC应该满足条件:______________________(直接添加条件,无需证明).
拓展培优
拓展角度1 利用特殊四边形的判定说明四边形的形状
10.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.www-2-1-cnjy-com
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
拓展角度2 利用特殊四边形的判定探究中点四边形的形状
11.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2-1-c-n-j-y
(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形.
(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,判断中点四边形EFGH的形状,并说明理由.2·1·c·n·j·y
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)21m
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
18.2.3正方形
第 2 课时 正方形的判定
夯基训练
知识点1正方形面积的性质
1.如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为___________.版权所有
2.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )1-cn-jy.com
A.4 B. C.2 D.2
知识点2 正方形的判定
3.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
题型总结
题型1 利用“一组邻边相等的矩形是正方形”证明四边形是正方形
如图,在Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
5.如图所示,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.21
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
题型2 利用“有一个角是直角的菱形是正方形”证明四边形是正方形
6.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形BECF是什么四边形?并说明理由;
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
7.如图所示, ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=____________时,四边形ACED是正方形.请说明理由. 21·世纪*教育网
题型3 正方形的性质和判定的综合应用
8. 如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.求证:
(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
9.如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平
分线于点E,交∠BCA的外角∠ACG的平分线于点F,连接AE、AF.
(1)求证:∠ECF=90°;
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
(3)在(2)的条件下,要使四边形AECF为正方形,△ABC应该满足条件:______________________(直接添加条件,无需证明).
拓展培优
拓展角度1 利用特殊四边形的判定说明四边形的形状
10.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.www-2-1-cnjy-com
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
拓展角度2 利用特殊四边形的判定探究中点四边形的形状
11.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2-1-c-n-j-y
(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形.
(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,判断中点四边形EFGH的形状,并说明理由.2·1·c·n·j·y
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)21m
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
